例谈计算教学中算法的有效建构

江苏省东台市东台镇四灶小学 申碗平

例谈计算教学中算法的有效建构

江苏省东台市东台镇四灶小学 申碗平

计算教学是小学数学教学的重要部分，在平时的计算教学中，教师常常忙于演示与讲解，忽视学生参与建构算法的心理历程。学生对算法的掌握仅仅停留在记忆与模仿上，学生不明白为什么这样算，为后继的学习埋下了很大的隐患。本文更关注学生建构算法的内部机制，试图结合一些实例谈谈如何更有效地帮助学生理解算理、掌握算法。

问题情境；表象操作；题组

笔者认为，要提升计算教学的有效性，教师要充分利用好结构化的问题情境，要合理搭建理解抽象算理的平台，要最大化地发挥题组功能。下面笔者结合苏教版三年级上册第一单元“除法”的教学谈谈计算教学中算法的有效建构。

一、充分利用结构化的问题情境，为理解算理、构建算法提供直观的帮助

问题情境的结构性是指问题情境的构建及其发展揭示的知识应有内在的逻辑结构。我们知道，结构化知识是最易于转化为认知结构的，而结构化的情境则为这种转化提供了心理空间，能促进这种转化，能够有效激发学生的问题意识和策略意识，激活学生的数学思维。教材从学生的最近发展区出发，精心设计数学问题情境的呈现方式，努力发挥数学问题情境的导向作用，促使学生亲身经历将实际问题抽象成形式化数学知识的过程，进而获得对有关概念、法则、性质和规律的理解，发展数学能力，增强问题意识和数学应用意识。因此，在计算教学中要十分重视引导学生观察情境图中具体的学习对象，发现有价值的信息，为理解算理、构建算法提供直观的帮助。

例如，教学三年级（上册）“两位数除以一位数的除法”时，教材创设了同学们买铅笔的问题情境，先教学整十数除以一位数的口算，再教学两位数除以一位数的笔算。

由于是第一次接触这样的口算和笔算，教材精心设计了问题情境的呈现方式，在以对话的方式呈现有关信息的同时，还出示了相应的铅笔图。图中的“4捆铅笔”即4个十和“4捆又6支铅笔”即4个十6个一，对口算和笔算的计算思路都有很好的暗示作用。在口算时，根据“4捆”的铅笔图，学生容易想到“把40支铅笔平均分给2个小朋友，就是把4捆铅笔平均分成2份，每份是2捆，是20支”。在笔算时，根据“4捆又6支”的铅笔图，学生容易想到把46支铅笔平均分给2个小朋友，可以先分整捆的，再分单根的；也可以结合上面学习的口算，想到“40÷2=20，6÷2=3，20+3=23”。两种思路都隐含着“先用两位数十位上的数除以一位数，再用个位上的数除以一位数的方法”。这就为进一步探索笔算方法提供了十分丰富的感性经验，为学生的自主探索提供可能，使学生“跳一跳”就能“摘到果子”。

二、充分利用表象操作，为计算方法的抽象搭建平台

著名教学心理学家布鲁纳的“表象认识论”指出，儿童的认知水平应经历三个阶段，即行为表征、表象表征、符号表征。也就是说儿童的学习应该从感知操作到形成表象再到形成形式化的符号表达。在由直观操作过渡到一般算法的过程中，需要重视表象操作这一中间环节。所谓表象操作，就是在具体实物操作的基础上，教师引导学生联系实物操作的方法和过程，在头脑中进行类似的操作。这样可以帮助学生摆脱具体实物的束缚，更好地构建比较抽象的算法。如果跳过这一环节，学生的算法构建容易与直观操作相脱节。

例如，教学三年级（上册）“首位不能整除的两位数除以一位数的笔算除法 ”的内容。主题画面中有5桶羽毛球和2个羽毛球，要求平均分给2个班，每班能分到多少个？学生很容易想到算式52÷2，学生尝试计算受挫。这时，教师不应急切板演讲解，应有序列地带领学生开展探索“52÷2=？”的活动。

第一层次，以实际动手操作积累表象操作的经验。教师课前准备5桶羽毛球和2个羽毛球，让学生动手分一分。当学生分整桶时，出现5桶不能正好分掉的问题，于是学生想到了“拆整桶”（这其实就是“退一当十”的数学原型），进而明白分单个的时候，不只是分画面中的2个，还有1桶里的10个，合计12个。在操作中他们能先分给每班2筒，再把余下的1筒羽毛球和另外2个合起来继续平均分。反复操作几次之后，进入表象操作。

第二层次，以表象操作的经验推进算法的建构。让学生脱离开羽毛球实物，动脑想把52个羽毛球平均分给2个班是如何操作的。（52÷2）学生在脑中表象出“分整桶”“拆整桶”“分单个”，进而将“分的过程”在头脑中数学化，实现实物单位“桶”“个”向计数单位“十”“个”的转变，最终实现由“分52个羽毛球”到“分52这个数”的思维跨越，明白被除数十位上余的是1个“十”，可以和个位上的2合成12继续除，突破学生思维瓶颈。进而形成“首位不能整除的两位数除以一位数的笔算除法”的计算方法：计算“52÷2”时要先算40÷2=20，再算12÷2=6，合起来就是26。在此表象操作基础上，学生联系竖式的写法和已有的计算过程，容易完成并理解以下的竖式。

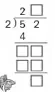
第三层次，由抽象的算法“反”想表象操作的过程。竖式形成后，引导学生思考：“竖式中的4是什么意思？”“竖式中5减4得1，这个1表示什么意思？”“商十位上的2是怎么得到的？商个位上的6又是怎么得到的？”通过“反”想活动，进一步帮助学生内化计算原理，使学生真正“摘到果子”。

［1］侯正海.在理解算理的基础上构建算法［J］.小学数学教学网，2010.

［2］楚平.问题情境——计算教学的活力源泉［J］.小学数学教学网，2011.