微积分在高中数学中的应用研究

贵州工程应用技术学院 曹发勇

微积分在高中数学中的应用研究

贵州工程应用技术学院 曹发勇

微积分在高中数学中占据着非常重要的作用，对培养学生的逻辑思维能力、想象能力和创新能力能够发挥重要的作用。本文针对高中数学中的关于极限、导数等难点，探讨微积分在解决这些难点中的应用方法，对微积分在高中数学的应用做出有益的思考。

微积分；高中数学；应用

微积分是数学科学的重要组成部分，由17世纪牛顿和莱布尼茨分别创立。微积分在描述变量和函数中起到了非常重要的作用。新《普通高中数学课程标准》中对微积分的教学内容进行了改革，通过在高中阶段使学生初步了解微积分的思想，为学生进入大学阶段学习高等数学打下良好的基础。本文通过例子，说明微积分在求解极值、函数单调性、方程求解等方面的应用。

一、利用微积分求解函数极值

微积分在求解函数极值中有着非常巧妙的应用。求解步骤为：（1）首先对函数f（x）求导f'（x）；（2）求解方程f'（x）=0的根；（3）判断f'（x）在f'（x）=0根的两边的符号，确定极值的类型。

解：f'（x）=lnx+1=0，可得x=1/e，而当x位于（0，1/e）时，f'（x）＜0，f（x）为减函数；当x位于（1/e，e］时，f'（x）＞0，f（x）为增函数。

可知：x=1/e，f（x）取极小值，f（x）取值为-1/e；当x=e时，取极大值，f（x）取值为e。

利用函数求导可以迅速判断出函数的极值。

二、利用微积分判断函数的单调性

函数单调性的判断是高中数学中一个非常重要的内容，也是历年高考重要的考点。利用函数求导后的正负，很容易判断出函数的单调性。

例2：（2009年广东卷文）函数f（x）=（x-3）ex的单调递增区间是（ ）。

A.（-∞，2） B.（0，3） C.（1，4） D.（2，+∞）

分析：对函数f（x）求导，f'（x）＞0的解即为单调递增区间。

f'（x）=ex+（x-3）ex=（x-2）ex＞0，可得x＞2。因此，本题选D。

三、利用微积分求证不等式

利用导数研究函数的单调性，再由单调性来证明不等式是函数、导数、不等式综合中的一个难点，也是近几年高考的热点。其主要思想是构造辅助函数，把不等式的证明转化为利用导数研究函数的单调性或求最值，从而证得不等式。

例3：当x位于（0，π）时，证明不等式sinx＜x成立。

分析：构建函数f（x）=sinx-x，对其求导，并判断导数的正负即可。

构建函数f（x）=sinx-x，求导可得f'（x）=cosx-1

由于x位于（0，π），因此f'（x）＜0。

因此f（x）=sinx-x在区间（0，π）上为单调减函数，而f（x）=0，

因此在x位于（0，π）时，f（x）＜0，

即sinx＜x成立。

四、利用微积分求解曲面面积

定积分是新课标中新加的内容，新《课标》对定积分的定位如下：（1）通过求曲边梯形的面积、变力做功等实例，从问题情境中了解定积分的实际背景；借助几何直观体会定积分的基本思想，初步了解定积分的概念，为以后进一步学习微积分打下基础；（2）通过实例，直观了解微积分基本定理的含义；（3）了解微积分的文化价值。可见，高中课程学习积分与定积分，重在粗浅地领略其主要思想和基本方法，从一些实例中初步认识定积分的工具作用。近年来，部分地区高考主要在定积分的求法、定积分的简单应用尤其是利用定积分求面积上做文章。

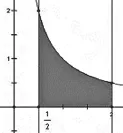
例4：（2008海南、宁夏卷理）由直线x=0.5，x=2，曲线y=1/x及x轴所围图形的面积是（ ）。

A.15/4 B.17/4

C.0.5ln2 D.2ln2

分析：此题是求连续曲线y=1/x，x轴二直线x=0.5，x=2，所围成的曲边梯形的面积。

五、利用微积分在数列问题中的应用

例5：求数列1，2x，3x2，…，nxn-1的和（其中x≠0，x≠1）。

分析：这道题可以用错位相减法求和，但若用导数方法运算会使问题更加简明。

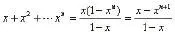
六、小结

微积分能够高速有效地解决很多数学问题，在高中数学中也有着广泛的应用。微积分自进入高中数学以来，对培养学生的数学思维方式提供了新的途径，也为帮助学生在进入大学后更好地学习微积分打下良好的基础。微积分在高中数学中有着广泛的应用，除了本文上述的领域之外，在方程求根、函数图像、切线方程和面积求解等领域也有着广泛的应用，值得进一步去探讨研究。

［1］许荣良.高中数学解题中微积分的应用［J］.数理化学习（高中版），2014（11）.

［2］张海燕.微积分在高中数学解题中的应用［J］.中学生数理化（学研版），2015（8）.

［3］王湘平.微积分在高中数学解题中的应用［J］.才智，2013（5）.

曹发勇（1991- ），男，贵州赫章人，汉族，本科学历，学士学位，数学与应用数学专业。）