依类比教学优化知识网络、提升迁移能力——以“线段与角”复习课为例

江苏省苏州学府中学 陈伟华

依类比教学优化知识网络、提升迁移能力
——以“线段与角”复习课为例

江苏省苏州学府中学 陈伟华

通过类比的方法教学，不仅有利于学生构建系统的知识结构、优化知识网络，也可以提高学生的迁移能力，达到事半功倍的效果。

类比；迁移；知识网络；线段与角

“类比”是根据两个不同的对象，但在某些方面（特征、属性、关系等）的类同之处，推测这两个对象在其他方面也可能有类同之处；“迁移”是利用新旧知识、新旧规律之间的相似、相通之处，将所学的方法应用到新情境中，解决新问题的一种能力。《义务教育数学课程标准》也指出：……通过观察、操作、归纳、类比、推断等数学活动，体验数学问题的探索性和挑战性，感受数学思考过程的条理性……

通过不同知识内容间的类比可以实现问题的迁移和化解，进而形成知识的广泛迁移能力，可以避免对知识的死记硬背，实现知识点之间的贯通理解和转换，有利于认识问题的本质和规律，构建知识结构网络，提高解决问题的灵活性和有效性。线段与角是平面图形的基础，它们之间有不少相似、相通之处。在复习时，笔者特别增加了一节从类比的角度来关注、辨析线段与角的复习课，取得了良好的教学效果。本文笔者以此为例，谈谈“类比”教学，与同行交流。

一、“线段与角”类比复习课过程简记

1.活动一：线段与角的大小类比

例1：如图1所示，估计线段AB与线段BC的大小关系，再用刻度尺或圆规来检验你的结论。

例2：如图2所示，估计∠AOB 与∠BOC的大小关系，再用量角器或圆规来检验你的结论。

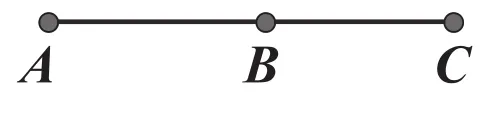
图1

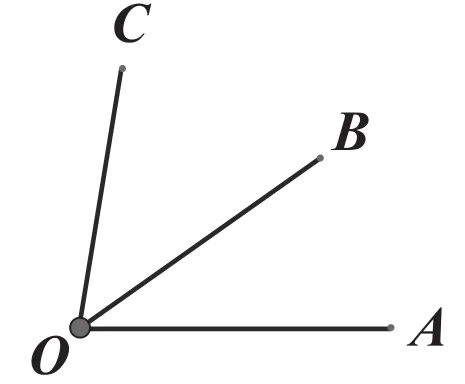
图2

简析：对于例1，我们可先用目测估计，再用度量法或叠合法。用度量法时，先用刻度尺量出线段AB与线段CB的长度，再做比较；用叠合法时，先用圆规量出线段AB的长，再用圆规的一端和点B重合，当另一端和点C重合时，AB=BC；否则，会有AB＜BC或AB＞BC。与例1类似，例2也可用目测估计、用量角器度量、用圆规叠合的方法。两个例题形式相同，答案相似。通过类比，学生感受到了不同问题之间的联系。

2.活动二：线段条数与角的个数类比

例3：如图3所示，在线段AB上取3个点C、D、E，则图中共有几条线段？在线段AB上取n个点呢？

例4：如图4所示，在∠AOB内部引3条射线OC、OD、OE，则图中共有几个角？在∠AOB内部引n条射线呢？

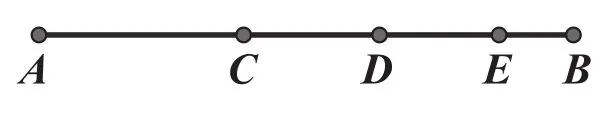
图3

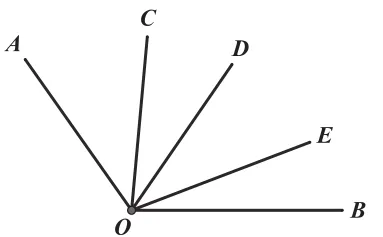
图4

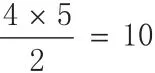
3.活动三：线段与角的和差关系类比

例5：如图5所示，点C、D在线段AB上，

则AD=________+________=________-________。

例6：如图6所示，在∠AOB内部引2条射线OC、OD，

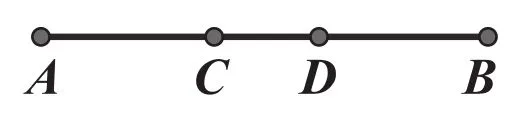
图5

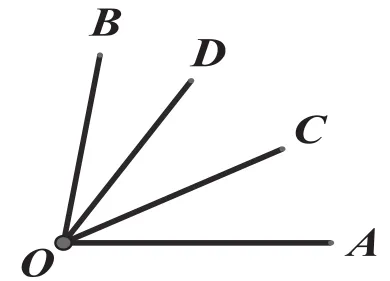
图6

则∠AOD =∠_____+∠_____=∠_____-∠_____。

简析：线段与角的和差关系是几何证明的基础，在证明的方法、策略、内容和形式上都具有相通性，都是将线段（或角）转化成若干条线段（或角）的和或差，从而解决问题。通过以上类比教学，学生的相关知识网络得到了优化，迁移能力得到了提升。

4.活动四：线段的中点与角的平分线类比

例7：如图7所示，点C在线段AB上，点D、E分别是线段AC、CB的中点，若AB=6，求DE的长。

图7

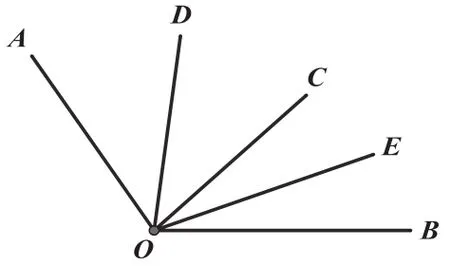
图8

例8：如图8所示，射线OC在∠AOB内部，射线OD、OE分别是∠AOC、∠BOC的平分线，若∠AOB=130°，求∠DOE的度数。

简析：在讲解例7时，老师可以先详细地复习与线段中点的相关知识点，特别是引导学生掌握其中最基本的几何语言，点D是线段AC的中点（中点的定义）。由于本题没有给出两条线段AC、CB的具体数值，只给出两条线段BC的和AB的长度，导致有的同学无从下手，有的同学只会写出结果，不能有条理地表达解题过程，，老师可以把以上解题过程进行板书。然后，让学生模仿例7来解答例8，并要求用规范的几何语言表达解题过程。通过类比，能较快提升学生使用数学语言表达问题的能力。

5.活动五：未知图形条件下的分类讨论

例9：若线段AB=6，点C在直线AB上，点D、E分别是线段AC、CB的中点，求DE的长。

例10 若∠AOB=130°，引一条射线OC，射线OD、OE分别是∠AOC、∠BOC的平分线，若∠AOB=130°，求∠DOE的度数。

简析：例9中，因为点C在直线AB上，而且图形又未知，因此，需要分类讨论三种情形：

情形1：当点C在线段AB上时，解得：DE=DC+CE=…=3

情形2：当点C在线段AB的延长线上时，解得：DE=DCCE=…=3

情形3：当点C在线段BA的延长线上时，解得：DE=CEDC=…=3

在复习中，很多同学由于考虑得不完备而漏掉一解，通过吃一堑长一智，在做例10时，同学们会变得更谨慎，达到了举一反三的目的，例10解略。

二、依类比教学优化知识网络、提升迁移能力

1.运用类比，构建系统的知识结构，优化知识网络

知识与技能的习得有同化和顺应两个过程，在习得的过程中有“不平衡”和“平衡”两种状态。若能巧妙地运用类比的方法进行迁移教学，不仅可以让习得的过程进行得更顺畅、更高效，还有利于学生保持习得内容长久稳定。数学知识是一个联系的整体，特别是有些并列的数学知识，它们研究的对象同类，研究内容相近，研究的方式相同，因而它们学习的经验可相互借鉴。我们可以合理地运用类比的策略，引导学生在类比中探究，在探究中掌握新知识，形成稳定、清晰且整体的知识网络。

线段与角是最简单、最基本的平面图形，是研究其他图形性质的基础。线段与角在它们的度量、条数个数、和差关系等性质的研究思路相同，如线段中点与角的平分线的定义、几何语言的表述和说理、运用等方面都可以进行类比。通过这种类比教学，学生不仅可以加深对这两种图形的认识，而且还可以体会到知识之间存在的关联，在头脑中形成鲜明、清晰的印象和知识结构，构建起知识网络，这为以后研究几何图形提供了方法和思路。

2.运用类比，引导学生感受研究不同知识时的方法联系

世界是广泛联系的，数学学科内的不同知识内容之间更是充满关联。旅美独立数学教育研究者马立平博士在名著《小学数学的掌握与教学》中曾指出：数学教学应追求数学知识的关联度、贯通度，并注重数学知识之间的深度与广度的理解。本课的教学设计做出了一些探索和努力，比如在每组例题的呈现上从形式与本质上都是相近的，让学生在整节课中都能感受到问题在形式上的关联。此外，问题在解法、变式等角度上的本质相通，如本文中的例1、例2中线段与角的大小类比，例7、例8中线段的中点与角的平分线等，通过类比，促进学生感受不同问题之间的联系。

3.运用类比，利于数学思想的渗透，进而促进学生迁移能力的提升

数学的思想方法是数学的灵魂，作为知识的数学离开学校可能不到两年就会忘记，唯有深深铭刻在学生头脑中的数学思想、研究方法和策略等，会发挥潜移默化的作用，使他们受益终身。因此，数学教学在关注知识、技能、方法的同时，应有意识地渗透基本数学思想，提升学生的迁移能力。

本节复习课将线段与角进行全方位的类比，让学生明确了线段与角学习的目标，带领学生理顺了学习的思路，真正让学习活动具有了思维的含金量。在增强思维的逻辑性与条理性的同时，让学生领悟到“平面图形”研究的一些“基本套路”，感悟“类比”的思想方法和学习策略。

总之，在教学过程中，教师要善于引导学生运用类比法，在类比中找出知识间的内在联系，合理运用类比的策略，引导学生构建系统的知识结构，优化知识网络，有利于知识的固化、活化；教师要善于激励学生在类比中探究，在类比中归纳，在类比中建构，从而提升学生触类旁通、举一反三的能力；教师要善于创造有类比问题的环境，引导学生提出问题并做出合理的猜想和假设，培养学生分析问题和解决问题的能力。

［1］江志杰.二次函数模型的迁移与类比［J］.中学数学研究，2016（2）.