高中数学解题教学中分类讨论思想的培养

江苏省口岸中学 韩 兵

高中数学解题教学中分类讨论思想的培养

江苏省口岸中学 韩 兵

在高中数学中，对于数学思想的学习掌握是很重要的。其中，分类讨论思想在高中数学解题教学中最为常用。在高中数学解题中，常常会遇到一些问题包含多种情况，这就需要学生应用分类讨论思想，将问题细化成多个部分，最后综合起来，得到最终的结果。

一、明确分类讨论思想应用标准

在应用分类讨论思想进行解题时，教师需要帮助学生明确其应用标准。首先，学生要全面理解题意，明确题目中需要分类讨论的具体情况。一般来说，在高中数学解题中，需要进行分类讨论的情况有以下几种：一些概念、公式、性质等条件具有分类的内容；含有参数的函数、方程、不等式等，因为参数的不确定性，会导致问题出现不同的情况；在进行几何问题的求解时，有些图形位置或图形形状无法确定，在不同情况下会有不同求解；排练组合问题中存在着一些特殊的情况。第二，教师要教授学生应用分类讨论思想的方法。科学严谨的分类讨论，必须达到一定的标准。在应用分类讨论思想时，学生需要明确分类标准、全面讨论分类的各个情况，做到不漏项、不重复，在题目中所需进行的分类讨论有多种对象时，要对问题进行分层讨论，清晰化解题思路。第三，应用分类讨论思想进行解题，需要在最后对分类的结果进行总结归纳。分类讨论思想的逻辑性很强，同样的，应用分类讨论思想进行解题也需要学生具有较强的分析能力和逻辑思维能力，学生在解题时要锻炼自身的解题意识，准确判断题目是否真的需要进行分类讨论。

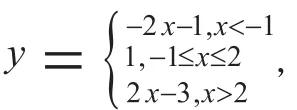
二、在解题中应用分类讨论思想

其一，分类讨论思想在概率问题中的应用。例如，有一集合M=｛0，2，4，6，8｝，任选M的两个非空子集A，B，要求集合A中最大的数都比集合B中最小的数小，有多少种选择的方法？对于这道题的求解，我们可以以A中最大的数为讨论对象进行分类讨论。①A中最大的数为0，即A=｛0｝，此时B最小的数只要比0大就可以了，总共有15种情况；②A中最大的数为2，此时A的组成可以有2种情况，B中最小的数需要满足大于2，则B有7种情况；③A中最大的数为4，此时A的组成可以有4种情况，B中最小的数需要满足大于4，则B有3种情况；④A中最大的数为6，此时A的组成可以有8种情况，B中最小的数需要满足大于6，则B有1种情况。综合四种条件下的选择，可以得到1×15+2×7+4×3+8×1=49，符合题目要求的共有49种情况。

其二，分类讨论思想在函数解题中的应用。函数作为高中数学的重点内容，有很多题目都需要应用分类讨论思想。例如，对于函数单调性的讨论，证明函数在（-1，+∞）上单调递增。对于函数单调性的求证，一般需要对函数进行求导，证明其导函数在区间上恒大于0。对于这道题，对原函数求导可得，分析其导函数特性，可以很容易发现只要将x的取值范围分成（0，+∞）以及（-1，0）两个部分进行分类讨论，然后就能求解出在这两个区间内大于等于0，在这两个区间内大于0，由此可知，导函数恒大于0，函数单调递增。又如，函数，如果当时，f（x）≥0恒成立，那么求a的值。根据题意，f（x）≥0，可以转换为，当x=0时，f（x）=1，当x>0时，在题目要求的区间内，，对不等式右半部分进行求导，可以得出其在x=1/2时取得最大值，为4，所以a≥4。当x<0时，，由于不等式右半部分在［-1，0］上单调递增，所以在x=-1时取得最小值，为4，故a≤4，综上可得，a=4。

分类讨论思想在其他很多类型的题目中都有应用，但其解题方法步骤一般都是一样的：首先，结合题目要求，判断是否进行分类讨论，选择分类讨论的对象以及分类讨论的各种情况；第二，按照标准进行合理的分类；第三，按照分类情况逐一进行求解；第四，对各种情况的结果进行总结归纳。总之，在高中数学教学中，教师要重视对分类讨论思想的教学，帮助学生熟练掌握，提高数学解题能力。