有关“三角形分割块数”问题的透视— —对《三角形与多边形分割》两篇文章的思考

江苏省苏州市工业园区娄葑学校 崔志刚

有关“三角形分割块数”问题的透视— —对《三角形与多边形分割》两篇文章的思考

江苏省苏州市工业园区娄葑学校 崔志刚

一、描述一下这类问题的内容及它的来龙去脉

第一篇文章简介：王海燕、王学贤、王申怀三位同志的《三角形与多边形的分割》［1］提出这样一个问题：把一个三角形各边n等分，连接各顶点和诸分点的线段，把三角形分割为多少块？

原文《三角形与多边形的分割》提出分割的块数公式

二、我在他们的基础上我提出一个解决这类问题的完整的看法，并回答相关的问题。

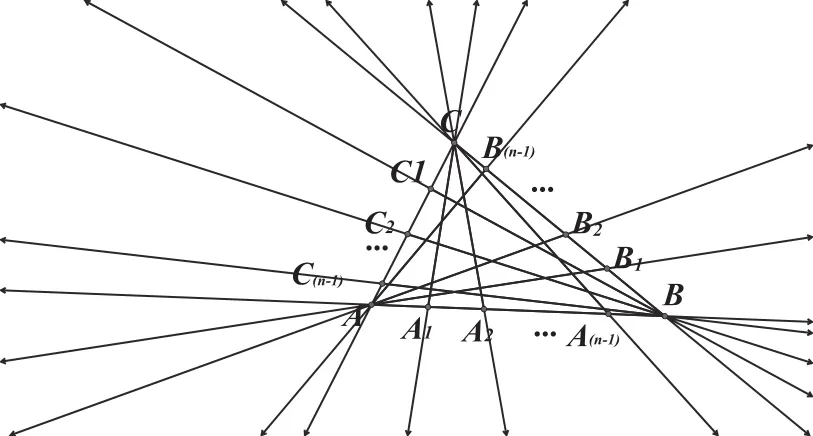
假如每边不是等份的话，那么可以实现任意三条分割线都没有交点，此时可分的块数计算（如图），我们可以把每条边和分割线延长为直线，拓展到整个平面内来思考。此时思路用整个3n条直线在没有共点的情况下可分为的块数减去三个顶点A、B、C处因共点而减少的块数再减去三角形外的块数即可得三角形内部被分为的块数。

那么在有三线共点的情况下，每出现一次，就减去一块。

在分割线有至少一条中线的情况下，有哪些共点的情况呢？

除中线外，其他的非中线的分割线讨论情况如何寻找呢？用死方法一个一个试，肯定很烦，不太实用。下面我们用寻找质因数的方法来解决。

下面以n=40为例。其质因数有2个：2、5；故可知（R）式的分子分母之和为20、8，其（R）式的分数可能为：

（1）当分子分母之和为20时，其可能的分数分别为：

通过（1）、（2）中的分数的组合（可以重复使用、可以将分数的分子分母颠倒计算）

可得24种三线共点情况。

如果考虑中线的情况，根据（Q）式可知有115种三线共点情况，故每边40等分时共可将三角形分割的块数为=4541块。

显然可知：如何准确地计算每边n等分后分割的块数不可能有一个具体的公式，因为关于一个数的因数，数论中没有一个明确的公式将一个数准确地分解为几个质因数的积；只能说用以上的方法可以求出来，但无法通过一个具体的公式求出三线共点的情况。

那么，如何能够知道n为哪些值的情况下有三线共点的情况呢？显然所有的偶数都有中线，因而都存在三线共点的情况。除了中线外，n为偶数时还有没有其他的呢？奇数呢？我们利用Excel采用如下的情况可以发现最小的奇数n为15，最小的偶数为20而不是文［2］所说的24，而且文章所列举的奇数、偶数还有很多。奇数有：15、35、45、55、63、65、75、85、91、99、105；偶数有：20、24、30、40、42、48、56、60、66、70、72、80、84、90、96、100。至于更大的n值，需要Excel计算的量更大即可解决。

［1］王海燕等.三角形与多边形分割［J］.数学通报，2006（08）.

［2］史立新等.《三角形与多边形的分割》一文的错漏［J］.数学通报，2012（04）.