关于两类color有序分拆的一个恒等式

郭育红

（河西学院数学与统计学院，甘肃 张掖　734000）

关于两类color有序分拆的一个恒等式

郭育红

（河西学院数学与统计学院，甘肃 张掖734000）

考虑了正整数n的有序分拆中，分部量1有两种形式的情形，发现正整数n的分部量1有两种形式的有序分拆数等于第2n+1个Fiboacci数F2n+1.进一步得到了一个涉及正整数n的分部量1有两种形式的有序分拆数与正整数的n-color有序分拆数之间的一个恒等式.并且给出了正整数n的分部量1有两种形式的有序分拆数的一个显式计数公式.

n-color有序分拆；Fibonacco数；恒等式；组合双射

1　引言

在经典的分拆理论中，MacMahon［1］第一次定义了正整数的有序分拆.即在正整数的分拆中考虑了分部量的次序.例如，4的无序分拆有：

共5个；而 4的有序分拆有：

共 8个.有序分拆也可以表示成向量的形式.例如，上述4的8个有序分拆可记为：

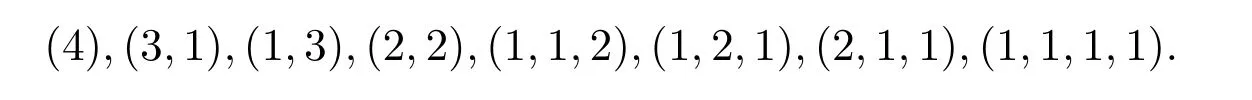
Agarwal和Andrews在文献［2］中拓广了正整数无序分拆的概念，给出了正整数的 n-color无序分拆.即在正整数ν的无序分拆中对于每一个分部量n着n种不同的颜色.他们将这n种颜色用下标表示为：n1，n2，···，nn.例如，3的n-color无序分拆有：共 6个.在2000年，Agarwal［3］又定义了n-color有序分拆.例如，3有8个n-color有序分拆：

近年来，对于正整数的 n-color有序分拆的研究产生了许多研究成果［3-13］.关于正整数的n-color有序分拆数有下面的结论.

定理1.1［3］设C（ν）表示ν的n-color有序分拆数，C（m，ν）表示ν分成m个分部量的n-color有序分拆数，C（m，q）和C（q）分别表示C（m，ν）和C（ν）的生成函数.则

这里Fn是第n个Fibonacci数.

定义1.1［3］Fibonacci数列是指：F0=0，F1=1，且满足：

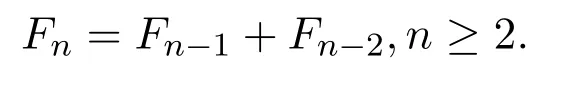
2013年，Shapcott在文献［14］中给出了正整数的n-color有序分拆的一种符号表示，他利用一串符号“×”和“-”表示正整数的n-color有序分拆，即对于正整数的n-color有序分拆的一个分部量λi，1≤i≤λ，用一串含有（λ-1）个-”和一个“×”的符号来表示，其中“×”所在的第i个位置表示分部量着第i种颜色；而两个分部量之间用一个“×”分割.例如，3的一个n-color有序分拆21+11可表示成：

利用这种“×”和“-”符号表示，Shapcott建立了正整数的n-color有序分拆数与正整数的分部量是1或 2的称为1-2有序分拆的分拆数、分部量是奇数的称为奇有序分拆的分拆数、分部量大于1的有序分拆数之间的一些恒等式.

2015年，Munagi和Sellers在文献［15］中给出了正整数的 Inplace有序分拆的几个恒等式.所谓正整数的有序分拆中分部量λ出现 Inplace j次是指在该分拆中，分部量λ连续出现j次.例如，分拆

就是一个偶分部量出现 Inplace偶数次的有序分拆.

同时，文献［15］中给出了下面的关于Inplace有序分拆的恒等式.

定理 1.2［15］设n≥1，正整数n的奇分部量出现Inplace偶数次的有序分拆数等于正整数2n的奇分部量有两种形式的有序分拆数.

在文献［15］中，作者将奇分部量有两种形式也看成一类color有序分拆，并将分部量λ有两种形式表示成：λ，λ∗.

本文考虑了正整数n的有序分拆中，分部量1有两种形式的情形，我们发现正整数n的分部量1有两种形式的有序分拆数等于第2n+1个Fiboacci数F2n+1.于是结合定理1.1中的（4）式给出的正整数的n-color有序分拆数与 Fibonacci数之间的关系，进而我们研究了这两类color有序分拆，得到了一个涉及正整数n的分部量1有两种形式的有序分拆数与正整数的n-color有序分拆数之间的一个恒等式.并且给出了正整数n的分部量1有两种形式的有序分拆数的一个显式计数公式.

2　主要结果

首先，讨论正整数n的分部量1有两种形式的有序分拆，我们仍沿用文献［13］中记号，即用1，1∗表示分部量1的两种形式.我们考虑其生成函数.

第2n+1个 Fibonacci数的生成函数是

于是，有下面的结论.

个Fibonacci数.则

这里ν＞0.

Fibonacci数与正整数的1-2有序分拆数之间存在着熟悉的关系式.

引理 2.1［14］设C1-2（ν）表示正整数 ν的1-2有序分拆数，Fn表示第n个 Fibonacci数.则

这里ν＞0.

自然地，我们考虑正整数n的分部量1有两种形式的有序分拆与1-2有序分拆之间的关系，容易得到了下面的一个恒等式.

定理 2.2设C21（ν）表示正整数ν的分部量1有两种形式的有序分拆数，C1-2（ν）表示正整数 ν的1-2有序分拆数.则

这里ν＞0.

我们给出该恒等式的组合双射证明.

证明我们将正整数ν的分部量1有两种形式的有序分拆分成以下两类：

（A）ν的分拆中分部量都是1；

（B）ν的分拆中分部量至少有一个不等于1.

对于（A）类中的有序分拆，按照Munagi和Sellers在文献［13］对定理1.2的证明中给出的对应关系：即把ν的分拆中分部量1对应成2ν的分拆的分部量2；把分部量1∗对应成2ν的分拆中的分部量“1，1”.我们知道，这类分拆对应着2ν的 1-2有序分拆中分部量1出现 Inplace偶数次的分拆.

对于（B）类中的有序分拆，仍然按照Munagi和Sellers的方法，把ν的分拆中分部量1对应成2ν的分拆的分部量2；把分部量1∗对应成2ν的分拆中的分部量1，1，把分部量λ＞1对应成2ν的分拆中的分部量2λ.于是我们知道这类分拆对应着2ν的不含大于1的奇分部量，且分部量1出现Inplace偶数次的分拆，但是不包括分拆

这时设

是2ν的不含大于 1的奇分部量，且分部量1出现Inplace偶数次的分拆，我们做如下变换：若λi=1，2，保留该分部量不变；当λi=2k，k＞1时，将λi分拆成：

这样我们就得到了2ν的1-2有序分拆，且分部量1不是出现Inplace偶数次的分拆.这是因为分拆α中如果有分部量1，则分部量1是出现Inplace偶数次的，而将与分部量1相邻的偶分部量2k分拆成形式

时，就破坏了分部量1出现的 Inplace偶数性；如果在分拆α中两个相邻的分部量都是大于2的偶数λi，λj，此时将λi，λj分拆成形式时，自然破坏了分部量1出现的 Inplace偶数性.

故（B）类中产生了2ν的1-2有序分拆中，分部量1不是出现Inplace偶数次的分拆.显然，该对应关系是一一的，反之亦然.

综合（A）类，（B）类知结论成立.接下来我们考虑正整数的n-color有序分拆，由定理1.1中的（4）式，得到下面的推论.

推论 2.1设C（ν）表示正整数ν的n-color有序分拆数，Fn表示第n个Fibonacci数.则

定理2.3设C′（ν）表示正整数ν的右端分部量不是11的n-color有序分拆数，C21（ν）表示正整数ν的分部量1有两种形式的有序分拆数.则

给出该关系式的组合证明.

证明事实上，由定理2.2我们知道：ν的分部量1有两种形式的有序分拆对应着2ν的右端分部量不是11的n-color有序分拆.接下来，我们用Shapcott在文献［12］中给出的方法再建立正整数2ν的1-2有序分拆与正整数ν+1的右端分部量不是11的n-color有序分拆之间的对应关系.对于2ν的任意一个1-2有序分拆，我们将分部量1表示成“×”，分部量2表示成“-”，就得到一个“×”和“-”符号图.然后在“×”和“-”符号图中考虑最右端的符号，如果最右端符号是“×”，我们将“×”换成“-”；如果最右端符号是“-”，我们就添上“×”.接下来，在得到的“×”和“-”符号图中按照从左向右的顺序将“×”和“-”符号图变换成正整数的n-color有序分拆，其中“×”所在的位置j表示分部量着j色，而两个相邻的“×”，右边的一个表示两个分部量的分割点.这样我们就得到了ν+1的右端分部量不是11的n-color有序分拆.这样我们就将ν的分部量1有两种形式的有序分拆对应到ν+1的右端分部量不是11的n-color有序分拆.反之亦然.故结论成立.

给出一个例子来说明上述对应关系.

例 2.1取ν=3，则3的分部量1有两种形式的有序分拆数与4的右端分部量不是11的n-color有序分拆之间的对应关系如下：

利用正整数ν的n-color有序分拆的计数公式

还得到了正整数ν的分部量1有两种形式的有序分拆数C21（ν）的显式计数公式.推论 2.2设C21（ν）表示正整数ν的分部量1有两种形式的有序分拆数.则

［1］MacMahon P A.Combinatory Analysis［M］.New York：AMS Chelsea Publishingvol，2001.

［2］Agarwal A K，Andrews G E.Rogers-Ramanujan identities for partition with'N copies of N'［J］.J.Comb.Theory A.，1987，45（1）：40-49.

［3］Agarwal A K.n-color compositions［J］.Indian J.Pure Appl.Math.，2000，31（11）：1421-1427.

［4］Agarwal A K.An analogue of Euler's identity and new Combinatorial properties of n-color com-positions［J］.J.Computational and Applied Mathematics，2003，160：9-15.

［5］Narang G，Agarwal A K.Lattice paths and n-color compositions［J］.Discrete Mathematics，2008，308：1732-1740.

［6］Guo Y H.Some n-color compositions［J］.Journal of integer sequence，2012（15）：1212.

［7］Guo Y H.n-color even compositions［J］.Ars Combina.，2013，109（2）：425-432.

［8］Narang G，Agarwal A K.n-color self-inverse compositions［J］.Proc.Indian Acad.Sci，2006，116（3）：257-266.

［9］Guo Y H.n-color even self-inverse compositions［J］.Proc.Indian Acad.Sci（Math.Sci.），2010，120（1）：27-33.

［10］Guo Y H.n-color odd self-inverse compositions［J］.Journal of integer sequence，2014，Vol.17：Article 14.10.5.

［11］郭育红.关于自反的n-colour有序分拆的一个关系式［J］.武汉大学学报：2012，58（5）：430-432.

［12］郭育红.关于正整数有序分拆的两个组合双射［J］.纯粹数学与应用数学，2016，32（1）：1-5.

［13］郭育红.关于正整数有序分拆的一些恒等式和n-colour有序分拆的两个组合性质［J］.纯粹数学与应用数学，2012，28（5）：590-613.

［14］Shapcott C.New bijections from n-color compositions［J］.Journal of Combinatorics，2013，4（3）：373-385.

［15］Munagi A O.Sellers J A.Some Inplace Identities for Integer Compositions［J］.Quaestiones mathematicae，2015，38（4）：535-540.

2010 MSC:05A17，05A19

A identity about two classes of color compositions

Guo Yuhong
（School of Mathematics and Statistics，Hexi University，Zhangye734000，China）

In this paper，we considered the compositions with the part 1 has two kinds，and found that the number of compositions with the part 1 has two kinds equals the（2n+1）thFibonacci number F2n+1.Furthermore，we obtained an identity between the number of compositions of n when part 1 can be of two kinds and the number of n-color compositions.And we also give an explicit counting formula of the number of compositions of n when part 1 can be of two kinds.

n-color compositions，the Fibonacci number，identity，combinatorial bijection

O157

A

1008-5513（2016）05-0441-07

10.3969/j.issn.1008-5513.2016.05.001

2016-07-22.

国家自然科学基金（11461020）.

郭育红（1970-），硕士，教授，研究方向：组合数学.