一类小周期椭圆方程的三重尺度渐近分析
黄志远,冯永平,易璇
(广州大学数学与信息科学学院,广东 广州 510006)
一类小周期椭圆方程的三重尺度渐近分析
黄志远,冯永平,易璇
(广州大学数学与信息科学学院,广东 广州510006)
利用三重尺度方法对一类小周期椭圆方程进行了三重尺度渐近展开分析,构造了对应的三重尺度形式渐近展开式,得到了均匀化常数和均匀化方程.在形式渐近展开的基础上,构造了对应边值问题解的三重尺度渐近近似解,并分析了对应三重尺度形式渐近误差估计.
椭圆方程;三重尺度方法;渐近展开
1 引言
自上世纪70年代,对某类小周期问题用传统数值计算需要进行精细网格剖分,从而使得求解线性方程组计算量非常大,为了克服这一困难,均匀化和双尺度渐近展开方法逐渐发展了起来.利用双尺度渐近展开思想得到了具有高阶震荡系数的渐近展开式并成功地降低了计算量[1].曹、崔[2]等人解决了一类有周期性局部约束且系数呈现小周期大幅度变化的椭圆型边值问题,同时也给出了整周期复合材料弹性结构的双尺度渐近分析.文献[3]中用双尺度方法给出具有小周期结构复合材料热力耦合问题的多尺度分析和有限元算法.
多尺度是先建立不同尺度的数学模型,再通过某些方法将不同尺度联系起来,可系统地分析材料的性能.多尺度方法在国内始于上世纪90年代,现阶段在计算机、生物医学、金属等领域的研究相对较多.1995年,杨卫等开始了微宏观断裂力学的研究,并取得一定的成果.2007年以前,许多研究细观模型的学者无法解释材料的显微结构和性能之间的关系,直到2007年,Tan[4]初步建立了水化模型与晶格断裂模型之间的联系.2009年李兆霞[5]等针对大型土木结构的多尺度模拟展开研究,实现了小尺度建模与大尺度建模的联系.文献[6]中通过引入细观尺度和宏观尺度,描述细观单胞的非均匀化构造和宏观均匀化结构,建立了复合材料内部温度场和位移场的双尺度表达式.但某些问题有更强的多尺度性,传统的双尺度展开方法已很难处理具有多重尺度的结构分析与评价.
在实际中经常碰到具有多重尺度的材料性能评价.特别地,不同的微观尺度和介观尺度的选取会对不均匀材料的力学性能分析有直接的影响作用.根据不均匀材料的多尺度表现,定义介观尺度部分的尺度元素为ε1=ε,其表示在介观尺度下最基本的尺度单元.定义微细观尺度部分的尺度元素为ε2=ε2,表示在微细观尺度下最基本的尺度单元.通常在数学上用下面的具有小周期系数的椭圆微分方程刻画具有多尺度性能材料的热传导行为:
2 θε(x)的三重尺度渐近展开式
将(1.3)-(1.5)式代入(1.1),逐次逐项进行整理后,其左端按ε的不同幂次可排列如下:
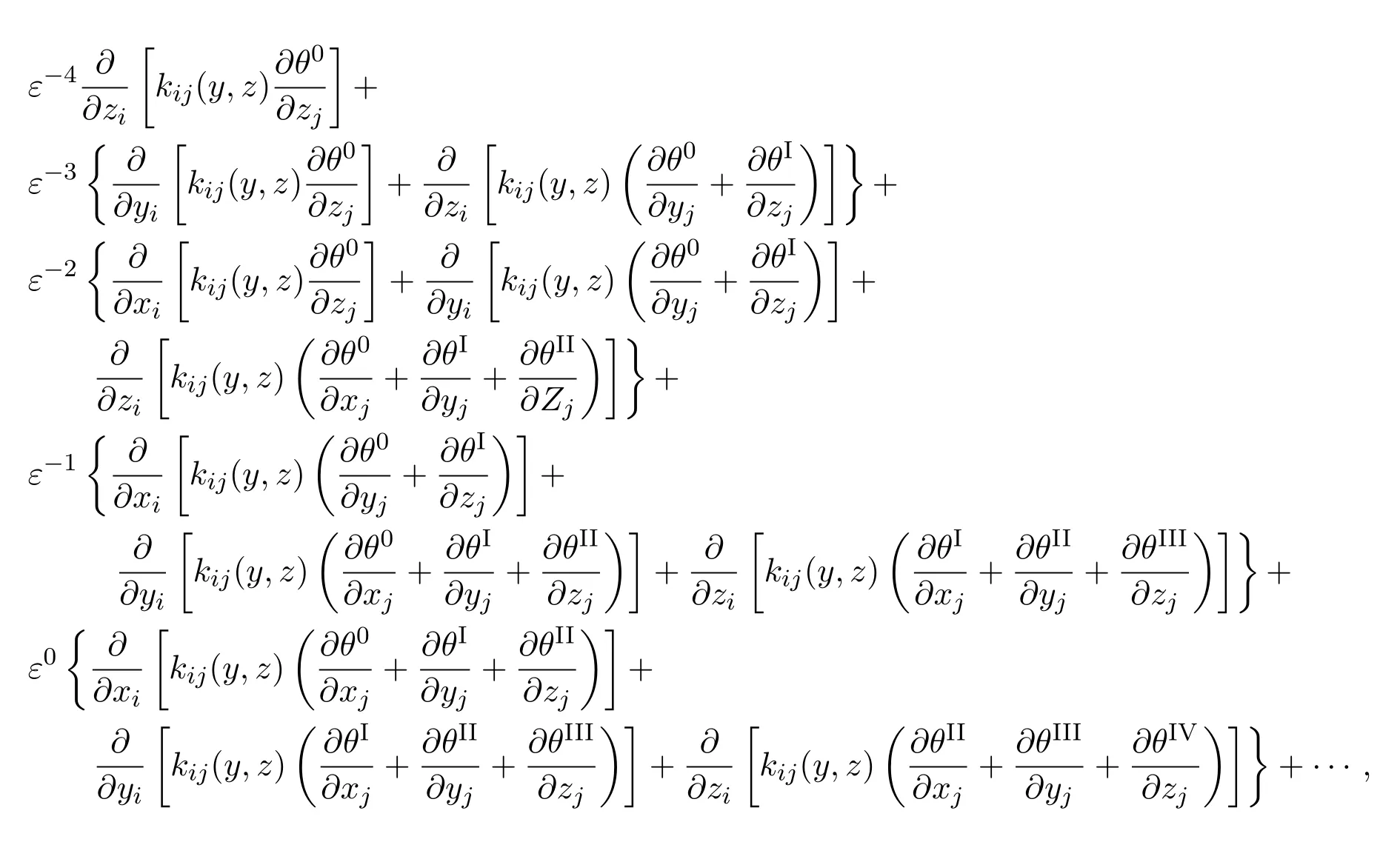
其右端项为-h(x).由于ε的任意性,比较等式两边ε-4,ε-3,ε-2,ε-1,ε0,···,的对应系数,得到下列等式,






定理 2.1假设 h(x),θ0(x)在 Ωε内足够光滑,则(1.1)存在如(1.2)形式的渐近解,其中(1)θ0(x)为均匀化解,由方程(2.24)确定.(2)θI(x),θII(x),θIII(x),θIV(x)分别由(2.7),(2.10),(2.18),(2.27)确定.为一级均匀化常数,由(2.17)确定.为材料的均匀化常数,由(2.25)确定.(4)θI(x),θII(x),θIII(x),θIV(x)中构造的小周期单胞函数分别由(2.12),(2.16),(2.19),(2.20)和(2.29)定解.满足相应的正则性条件.
3 θε(x)的渐近误差估计
在实际计算中经常运用如下的近似渐近计算公式:

对上式近似解,有以下的近似渐进误差估计.
定理3.1设θε(x)是问题(1.1)的弱解,如果θ0(x)∈H3(Ω),h(x)∈H2(Ω),则有


4 结论
对具有三重尺度的小周期椭圆问题,鉴于传统的均匀华方法与双尺度方法很难得到其解的渐近表示.利用逐次构造的方法,构造性地得到了相应的三重尺度渐近展开.对于该展开,分析了其相应的渐近近似解,讨论了其近似解的误差估计.理论上,于其均匀化性能分析建立了相应的分析依据.在数值计算中为构造相应的多尺度算法提供了理论依据.
[1]王自强,宋士仓,曹俊英.小周期复合材料热传导问题的双尺度渐近展开及收敛性分析[J].高校应用数学学报:A辑,2008,02:145-152.
[2]Cao L Q.Asymptotic expansion and convergence theorem of control and obser-vation on the boundary for second-order elliptic equation with highly oscillatory coefficients[J].Math.Model and Meth.in Applied Sci.,2004,14(3):417-437.
[3]Feng Y P,Cui J Z.Multi-scale analysis for the structure of composite materials with small periodic configuration under condition of coupled thermoelasticity[J].Acta Mechanica Sinica,2003,19(6):585-592.
[4]Tan Likun.Failure Mechanisms in Hydrating Cement Particle Systems[D].Delft University of Technology:Delft University Press,2007.
[5]孙正华,李兆霞,陈鸿天.大型土木结构的结构行为一致多尺度模拟――模拟方法与策略[J].计算力学学报,2009(6):886-892.
[6]吴世平,唐绍锋,梁军等.周期性复合材料热力耦合性能的多尺度方法[J].哈尔滨工业大学学报,2006,12:2049-2053.
[7]Guan X F,Liu X,Jia X et al.A stochastic multiscale model for predicting the mechanical properties of fiber reinforced concrete[J].International Journal of Solids and Structures,2015,56:280-289.
[8]Feng Y P,Cui J Z.Multi-scale fe computation for the structures of composite materials with small periodic configuration under condition of coupled thermoelasticity[J].Acta Mechanica Sinica,2004(1):54-63.
[9]刘晓青,曹礼群,崔俊芝.复合材料弹性结构的高精度多尺度算法与数值模拟[J].计算数学,2001(3):369-384.
2010 MSC:35J15
The asymptotic expression based on the triple-scale method for one class of small periodic elliptic equation
Huang Zhiyuan,Feng Yongping,Yi Xuan
(School of Mathematics and Information Sciences,Guangzhou University,Guangzhou510006,China)
By means of the triple-scale method the asymptotic expression for one class of small periodic elliptic equation is analyzed.Firstly,the formal asymptotic expansion is constructed,and the homogenization constants and equation are obtained.Then based on formal asymptotic expansion the asymptotic approximation solution is constructed and the corresponding error is analyzed.
elliptic equation,triple-scale method,asymptotic expansion
O178
A
1008-5513(2016)05-0495-10
10.3969/j.issn.1008-5513.2016.05.001
2016-06-20.
国家自然科学基金资助项目(11671304);广州市属高校科技计划基金(1201430652).
黄志远(1991-),硕士生,研究方向:应用偏微分方程.
冯永平(1975-),博士,教授,研究方向:偏微分方程数值解.

