NSD 序列加权和的中心极限定理及其在EV回归模型中的应用

余云彩，胡宏昌

（湖北师范大学数学与统计学院，湖北 黄石　435000）

NSD 序列加权和的中心极限定理及其在EV回归模型中的应用

余云彩，胡宏昌

（湖北师范大学数学与统计学院，湖北 黄石435000）

基于负超可加相依（简称为NSD）随机序列的性质及其一些不等式，利用随机变量的截断方法建立了NSD随机序列加权和的中心极限定理，从而推广了负相协NA随机序列的相应结论.并将其应用到变系数EV回归模型，得到了未知参数LS估计的渐近正态性.

NSD随机序列；中心极限定理；EV回归模型；LS估计

1　引言

随着NA随机序列的广泛研究，NSD这类较NA序列更为广泛的随机变量列逐渐得到重视.然而，许多NSD 随机序列的统计性质与NSD随机序列加权和的收敛性有着密不可分的关系，如线性回归模型中待估参数的渐近正态性，以及其大偏差性质等.因此，研究NSD随机序列加权和的中心极限定理并应用到EV回归模型中具有重大的理论与实际意义.

定义1.1［1］函数ϕ：Rn→R，如果对所有的向量x，y∈Rn，满足

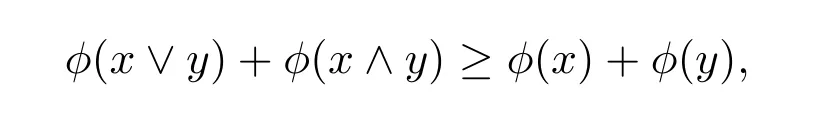
其中，“∨”代表两者之间的最大值，“∧”代表两者之间的最小值，则称ϕ为超可加函数.

定义1.2［1］称随机序列｛X1，X2，···，Xn｝为NSD序列，如果满足

其中，X∗1，X∗2，···，X∗n是相互独立的随机变量，对每个t，X∗t与Xt有相同的分布，ϕ是超可加函数，并且使得其期望存在.

NSD的概念最先由 Hu［1］引进，文章指出 NSD不蕴含 NA（Negative Association），C-hristofides［2］指出 NA蕴含 NSD.针对 NSD随机序列加权和的强稳定性研究，Shen［3］给出了 NSD随机变量的 Rosenthal型矩不等式，并建立了 NSD随机变量和的强收敛性.Eghbal［4］给出了NSD随机变量加权二次型形式的两个极大值不等式和强大数定律.Wang［5］探究了NSD随机变量加权和的完全收敛性，并且把结果应用到误差为NSD 的EV回归模型中，证明了LS估计的完全一致性.Wang［6］加强对矩的约束，讨论了误差为NSD的线性回归模型的M估计的强相合性.本文则是在一定条件下探究NSD随机序列加权和的中心极限定理，并将之应用到EV回归模型中，讨论未知参数LS估计的渐近正态性.

考虑如下误差为NSD的简单线性变系数EV模型：

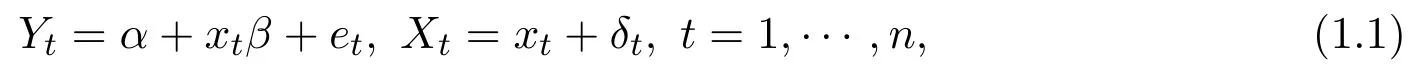
其中，Yt，Xt，t=1，···，n为可观测变量，xt，···，n为未知变量，α，β是未知参数，

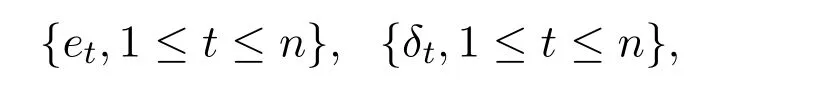
为两个独立的NSD随机变量序列.

模型（1.1）可写成如下形式：

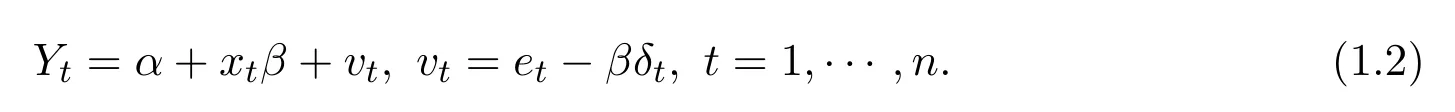
计算可得，α，β的LS估计为：

其中

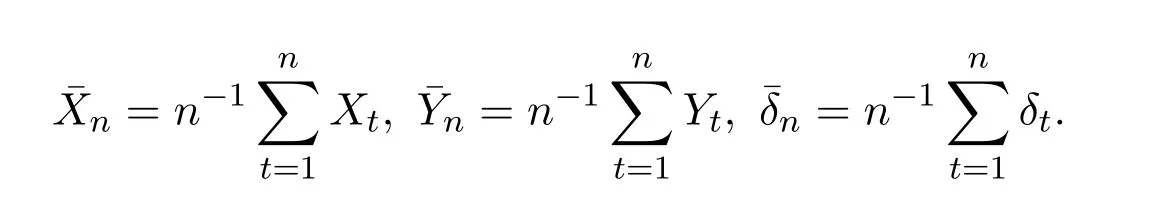
变系数EV回归模型由Deaton［7］提出之后，其渐近性得到广泛关注.在误差独立的情形下，Cui［8］证明了EV模型M估计的渐近正态性.Miao［9］建立了简单线性变系数EV模型LS估计的中心极限定理.Miao［10］得到了变系数EV模型未知参数LS估计的中偏差原理.Liu［11］证明了LS估计的一致性，得到强收敛与弱收敛具有等价性的结论，并证明具有相合性的充要条件是

然而在实际中，独立条件过于理想，学者们将视野拓展到相依误差下EV模型的研究.Fan［12］在误差项为平稳 α混合序列的情形下，得到了 EV模型 LS估计的渐近正态性.在误差为平稳 NA序列的情形下，Miao［13］讨论了EV模型LS估计的强相合和渐近正态性.Hu［14］在AR（1）误差下建立了EV模型Huber-Dutter估计的渐近正态性.胡宏昌［15］研究了AANA随机序列加权和的强收敛速度.在误差为严平稳NSD序列的情形下，Wang［6］讨论了EV模型LS估计的完全收敛性.作为NSD序列加权和中心极限定理的一个应用，本文考虑如下模型：

其中，｛et，1≤t≤n｝，｛δt，1≤t≤n｝均为平稳的NSD随机序列，并有

2　主要结果

定理 2.1设｛Xj，j≥1｝为NSD随机变量序列满足如下条件：

注2.1条件（A1）是对误差项最基本的假设.条件（A2）和（A3）在相依误差的研究问题上经常使用，如Baek［16］，Liang［17］针对NA随机变量序列加权和的中心极限定理时提出了此条件.条件（A4）是对权的一个常见约束，Liang［17］用到了此条件，所以我们所提出的条件是合理且容易满足的.

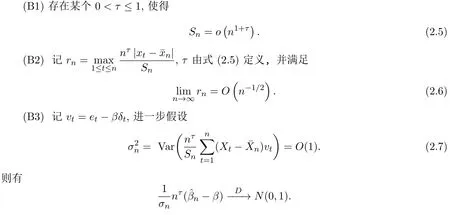
定理2.3在定理2.1的条件下，如果满足

则有

注2.2条件（B1），（B2）满足式（1.3），Miao［13］在证明误差为严平稳NA序列的EV模型LS估计渐近正态性时用到，并且文中要求这一比较强的条件，Wang［6］在讨论误差为严平稳NSD序列的EV模型LS估计强收敛性时也有用到.条件（B3）中vt为NSD随机变量，可看作一个无穷小的权，这里要求其方差有界较为合理，如NA这类特别的NSD随机序列在严平稳和τ=1时，就有条件（2.7），详细见Miao［13］.条件（2.8）事实上只需有界即可，故本文的条件较为合理.

3　定理的证明

上述定理的证明需要如下重要引理，在证明过程中C，C1，C2均表示绝对常数.

引理3.1［1］设｛X1，X2，···，Xn；n≥1｝是 NSD随机序列 ，则有下列性质：

（1）f1，f2，···是非降的连续函数 ，则 ｛fn（Xn），n≥1｝仍是 NSD随机变量序列.

（2）｛-X1，-X2，···，-Xn｝仍是NSD随机变量序列.

（3）对任意的x1，x2，···，xn都有

（4）假设｛Yn，n≥1｝为NSD随机序列，并且｛Xn，n≥1｝与｛Yn，n≥1｝间相互独立，那么｛X1+Y1，X2+Y2，···，Xn+Yn｝仍是NSD随机变量序列.

引理3.2［3］设｛Xn，n≥1｝是NSD随机序列，满足EXj=0，对某个p≥2，有E|Xn|p＜∞，那么对于所有n和p≥2，存在只依赖于p的正数Cp，使得

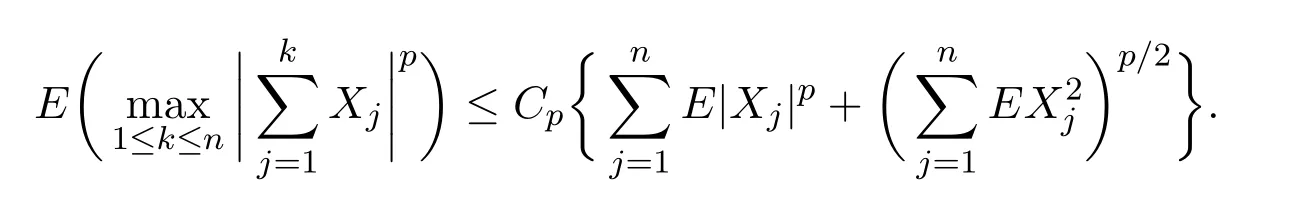
引理3.3［18］设（X，Y）是NSD随机变量，其联合分布为F（x，y），X和Y的边缘分布分别是FX（x），FY（y），如果E|XY|，E|X|和E|Y|都有界，那么

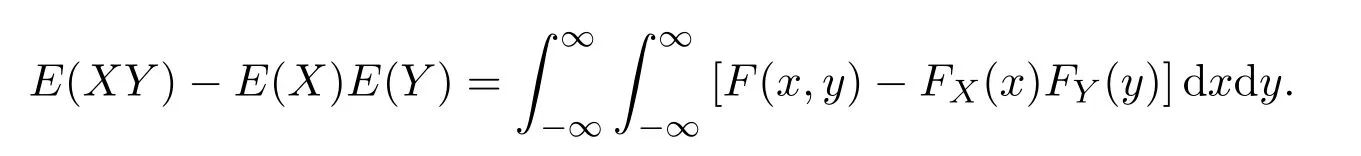
引理3.4设X1，···，Xn为NSD随机序列，满足则对任意实数rj， j=1，···，n，都有

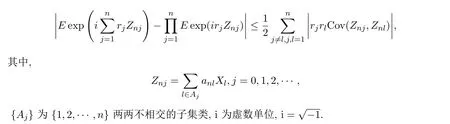
现取f（X）=exp（irX），g（Y）=exp（isY），那么‖f′（X）‖∞≤1＜∞，‖g′（Y）‖∞≤1＜∞，所以由式（3.3）可知，对任意的实数r，s都有

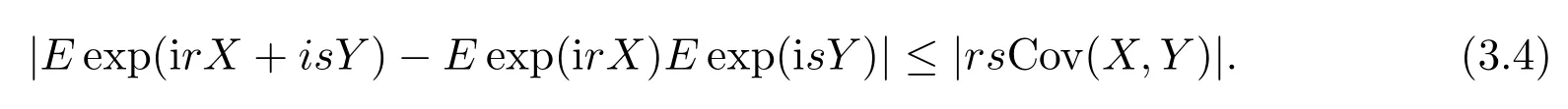
下面采用数学归纳法

I）当n=1时，由条件（A1）知，结论成立.

II）当n=2时，由式（3.4）可知，结论也成立.

III）当n＞2时，假设对所有的n≤M都使得结论成立，令n=M+1.

假设ε2=1，δ2=1，k∈｛1，···，M｝，所以总存在这样的值，使得

引理3.5［19］假设对每个一致度量ρ满足∀ε＞0，有

［1］Hu T Z.Negatively superadditive dependence of random variables with applications［J］.Probab.Stat.，2000，16：133-144.

［2］Christofides T C，Vaggelatou E.A connection between supermodular ordering and positive/negative association［J］.Multivar.Anal.，2004，88：138-151.

［3］Shen A T，Zhang Y，Volodin A.Applications of the Rosenthal-type inequality for negatively superadditive dependent random variables［J］.Metr.，2015，78：295-311.

［4］Eghbal N，Amini M，Bozrgnia A.Some maximal inequalities for quadratic forms of negatively superadditive dependence random variables［J］.Stat.Probab.Lett.，2010，80：587-59.

［5］Wang X J，Shen A T，Chen Z Y.Complete convergence for weighted sums of NSD random variables and its application in the EV regression model［J］.TEST，2015，24：166-184.

［6］Wang X H，Hu S H.On the strong consistency of M-estimates in linear models for negatively superadditive dependent errors［J］.Aust.New Zealand J.Stat.，2015，57（2）：259-274.

［7］Deaton A.Panel data from a time series of cross-sections［J］.J.Econ.，1985，30：109-126.

［8］Cui H J.Asymptotic normality of M-estimates in the EV model［J］.J.Syst.Sci.Math.Sci.，1997，10：225-236.

［9］Miao Y，Yang G Y，Shen L M.The central limit theorem for LS estimator in simple linear EV re-gression models［J］.Commun.Stat.，Theory Methods，2007，36：2263-2272.

［10］Miao Y，Wang K，Zhao F F.Some limit behaviors for the LS estimator in simple linear EV regre-ssion models［J］.Stat.Probab.Lett.，2011，81：92-102.

［11］Liu J X，Chen X R，Consistency of LS estimator in simple linear EV regression models［J］.Acta.Math.Sci.，2005，25：50-58.

［12］Fan G L，Liang H Y，Wang J F.Asymptotic properties for LS estimators in EV regression model with dependent errors［J］.AStA Adv.Stat.Anal.，2010，94：89-103.

［13］Miao Y，Zhao F F，Wang K.Asymptotic normality and strong consistency of LS estimators in the EV regression model with NA errors［J］.Stat.Papers，2013，54：193-206.

［14］Hu H C.Asymptotic normality of Huber-Dutter estimators in a linear EV model with AR（1）proc-esses［J］.J.Inequal.Appl.，2014，474：1-25.

［15］胡宏昌.加权AANA随机变量和的一致强收敛速度［J］.纯粹数学与应用数学，2014，30（6）：558-563.

［16］Baek J，Liang H Y.Asymptotics of estimators in semi-parametric model under NA samples［J］.J.Stat.Plan.Inference，2006，136（10）：3362-3382.

［17］Liang H Y，Zhang D X，Baek J.Convergence of weighted sums for dependent random variables［J］.J.Korean Math.Soc.，2004，41：883-894.

［18］Newman C M.Normal fluctuations and the FKG inequalities［J］.Comm.Math.Phys.，1980，74：119-128.

［19］Billingsley P.Convergence of Probability Measures［M］.NewYork：Wiley，1968.

2010 MSC:62F12

A CLT for weighted sums of NSD random sequences and its application in the EV regression model

Yu Yuncai，Hu Hongchang
（School of Mathematics and Statistics，Hubei Normal University，Huangshi435000，China）

By using the properties and some inequalities of negatively superadditive dependent（NSD）random sequences and the trunkated method，a central limit theorem for weighted sums of NSD random sequences is discussed，which generalizes and improves corresponding conclusions for negatively associated（NA）random sequences.As an application，the asymptotic normality of LS estimators of the unknown parameters in the variable coefficients EV regression model with NSD errors is obtained as well，which generalizes corresponding conclusions of negatively associated random sequences.

NSD random sequences，central limit theorem，EV model，LS estimators

O 212.1

A

1008-5513（2016）05-0525-11

10.3969/j.issn.1008-5513.2016.05.009

2016-04-29.

国家自然科学基金（11471105）；湖北师范大学优秀创新团队资助项目（T201505）.

余云彩（1990-），硕士生，研究方向：回归分析，时间序列分析.