一类指数型函数的性质及其应用
王 江 林慧敏
(湖北省团风中学,438800)
一类指数型函数的性质及其应用
王江林慧敏
(湖北省团风中学,438800)
最近,在教学中发现,形如y=a|x-m|+b(a>0,a≠1)的指数型函数,在近几年的各地高考题、模拟题中屡见不鲜.考查形式有判断函数图象、求最值、求参数范围、比较大小、解不等式等等. 解决这类指数型函数问题的关键是利用函数图象的性质.
一、一个重要结论
结论函数f(x)=a|x-m|+b(a>0,a≠1)的图象关于直线x=m对称.
证明设P(x0,y0)是函数f(x)=a|x-m|+b(a>0,a≠1)图象上的任意一点,则
f(x0)=a|x0-m|+b=y0.
点P关于直线x=m的对称点为Q(2m-x0,y0).
∵f(2m-x0)=a|2m-x0-m|+b
=a|x0-m|+b=f(x0)=y0,
∴点Q(2m-x0,y0)也在函数f(x)=a|x-m|+b(a>0,a≠1)的图象上.即函数f(x)=a|x-m|+b(a>0,a≠1)的图象关于直线x=m对称.
同时,我们也可以直接作出f(x)=a|x-m|+b(a>0,a≠1)的图象,观察其图象知,f(x)的图象关于直线x=m对称,并且有:
当a>1时,如图1,f(x)在(-∞,m)上单调递减,在(m,+∞)上单调递增,且f(x)的最小值为f(m)=1+b,值域为[1+b,+∞);
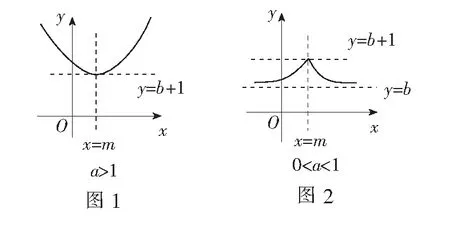
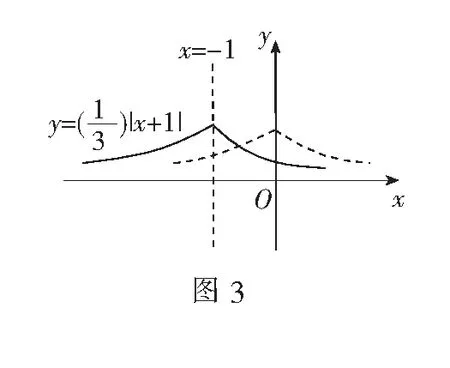
当0 例1(2012年上海高考题)已知函数f(x)=e|x-a|(a为常数),若f(x)在区间[1,+∞)上是增函数,则a的取值范围是______. 解易知函数f(x)=e|x-a|的图象关于直线x=a对称. 令t=|x-a|,则t=|x-a|在[a,+∞)上单调递增,又y=et为单调增函数,所以若函数f(x)=e|x-a|在[1,+∞)上是增函数,则有[1,+∞)⊆[a,+∞),所以a≤1,即a的取值范围为(-∞,1]. 评注这里利用了复合函数的单调性(“同增异减”)确定函数的单调区间,从而确定a的取值范围. 例2(2015年福建高考题)若函数f(x)=2|x-a|(a∈R)满足f(1+x)=f(1-x),且f(x)在[m,+∞)上单调递增,则实数m的最小值等于______. 解∵f(x)=2|x-a|(a∈R),∴f(x)的图象关于直线x=a对称. 又由f(1+x)=f(1-x)得函数f(x)的图象关于直线x=1对称,∴a=1, 由复合函数的单调性,得f(x)在[1,+∞)上递增, ∴[m,+∞)⊆[1,+∞),故m≥1, ∴实数m的最小值等于1. 评注本题还是抓住函数f(x)=a|x-m|+b(a>0,a≠1)的图象关于直线x=m对称求解.可以看出,这道高考题实则是2012年上海高考题的同类变式题. 例3(2015年天津高考题)已知定义在R上的函数f(x)=2|x-m|-1(m为实数)是偶函数,记a=f(log0.53),b=f(log25),c=f(2m),则a,b,c的大小关系为() (A)a (C)a 解∵f(x)=2|x-m|-1为偶函数,而它的图象又关于直线x=m对称, ∴m=0. ∴f(x)=2|x|-1,f(x)在(0,+∞)上单调递增. 又a=f(log0.53)=f(|log0.53|)=f(log23),b=f(log25),c=f(0), ∴b=f(log25)>a=f(log23)>c=f(2m)=f(0),即b>a>c,故选B. 评注本题先直接利用函数的图象特征,求出m的值为0,再结合函数的单调性比较大小,属于中档题. (1)作出图象; (2)由图象指出其单调区间; (3)由图象指出当x取什么值时函数有最值. 解(1)方法1由函数解析式,可得 其图象由两部分组成,如图3所示: 另一部分是:y=3x(x<0) (2)由图象知函数在(-∞,-1]上是增函数,在[-1,+∞)上是减函数. 评注本题考查了形如f(x)=a|x-m|+b(a>0,a≠1)这类指数型函数的图象及性质,通常解法是利用绝对值意义,分段讨论转化为指数型的分段函数,再通过函数图象变换求解;而直接利用其函数图象关于直线x=m对称的性质求解,显得快速简单,应当熟练掌握这类函数的图象性质. 综上,解答形如f(x)=a|x-m|+b(a>0,a≠1)类函数题时,只要充分抓住其图象关于直线x=m对称即可. 一个题型出现一次,也许仅仅是一个题型,但多次出现就可能是一个性质、一个规律、一个高频考点,学习数学要做一个细心的“有心人”,要善于观察发现、归纳总结和思考领悟. 1.已知函数f(x)=2|2x-m|+1(m为常数),若f(x)在区间[2,+∞)上是增函数,则m的取值范围是______. 3.已知函数f(x)为偶函数,且f(x)=f(x-4).又 (A)(-∞,2](B)[2,+∞) (C)[-2,+∞) (D)(-∞,-2] 参考答案 4.B; f(0)+a=a-1<0,f(2)+a=a≥0, 因此,存在唯一t∈(0,2],使得二、应用举例
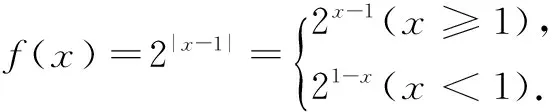


三、巩固练习