基于人工蜂群算法的车辆主动悬架LQG控制设计
张海涛
(安徽机电职业技术学院 汽车工程系,安徽 芜湖 241002)
基于人工蜂群算法的车辆主动悬架LQG控制设计
张海涛
(安徽机电职业技术学院 汽车工程系,安徽 芜湖 241002)
针对2自由度1/4车体汽车悬架LQG最优控制模型,综合局部精英策略局部搜索能力强和人工蜂群算法全局搜索效率高的优点,提出基于局部精英策略人工蜂群算法确定其加权系数的优化方法。利用Matlab/Simulink仿真软件,以积分白噪声模型作为地面输入和单位阶跃输入为路面输入模型,分别将传统LQG控制、人工蜂群算法LQG控制和局部精英策略人工蜂群算法LQG控制进行仿真和对比分析,结果表明,局部精英策略人工蜂群算法LQG控制方法可改善汽车的行驶平顺性和操纵稳定性。
振动与波;LQG最优控制;加权系数的优化;动态子群策略;人工蜂群算法;搜索能力
悬架作为汽车的重要组成部分,其性能的好坏,对汽车行驶平顺性、操纵稳定性和舒适性有很大的影响。目前对汽车悬架的研究热点集中在主动悬架的控制策略上,其中线性二次型最优控制算法比较成熟,应用比较广泛,该控制策略的性能完全取决于状态变量和输入变量的加权系数矩阵,加权系数矩阵没有固定解析方法,完全靠设计者经验经过多次调整来来获得加权系数值。这种方法不仅费时,而且无法保证获得最优权值矩阵使悬架系统达到最优。如孟杰等提出利用遗传算法获得悬架LQG控制器的加权系数矩阵[1];陈双等提出利用遗传粒子群算法获得加权系数矩阵[2];桑楠等提出利用遗传算法对汽车主动悬架控制器优化设计[3];李伟平等提出自适应模糊控制在磁流变半主动悬架中的应用[4];张立军等将参数灵敏度引入车辆半主动悬架控制系统中[5]。张磊等提出利用功率反馈主动控制算法对悬挂系统性能的影响[6];
本文将动态子群策略应用于人工蜂群算法中对汽车主动悬架LQG控制器的加权系数进行优化,利用动态子群策略局部搜索能力和人工蜂群算法全局搜索能力强的特点,以主动悬架的性能指标作为目标函数对权值系数矩阵进行优化设计,通过2自由度1/4车体汽车悬架控制的仿真,验证控制策略的正确性和有效性。
1 1/4车体悬架模型
2自由度1/4车体主动悬架模型如图1所示。图中m0为非簧载质量,m1为车体质量,k0为轮胎刚度,k1为悬架弹簧刚度,c1为减振器阻尼,x0为地面的扰动输入位移,x1为非簧载质量的位移,x2为车体质量的位移,u为悬架控制力。
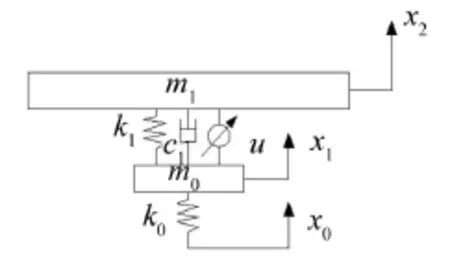
图1 1/4车体主动悬架模型
根据达朗贝尔原理可列出2自由度1/4车体主动悬架动力学运动微分方程,其中式(1)为1/4车体运动微分方程,式(2)为悬架非簧载质量的运动微分方程。
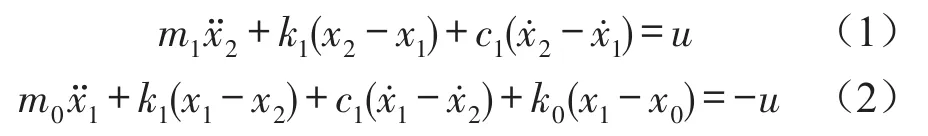
设状态变量
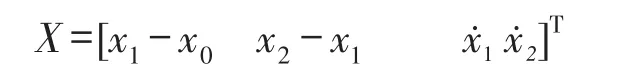
则系统的状态方程为
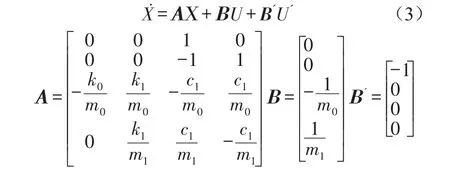
2 动态子群策略人工蜂群算法LQG控制器设计
2.1车辆主动悬架LQG控制器设计
对于2自由度1/4车辆悬架系统,LQG控制设计中的目标性能指标J可表示为车身垂向加速度̈2、悬架动挠度(x2-x1)、轮胎动位移(x1-x0)和悬架控制力u的加权平方和的积分值,即悬架综合性能指标J
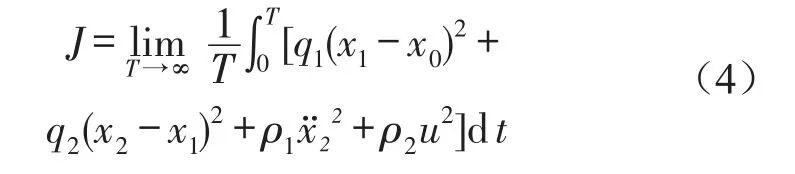
式(4)的矩阵形式
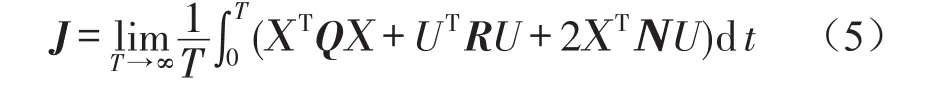
其中Q为状态加权正定矩阵,R为控制加权正定矩阵,N为状态加权正定矩阵和控制加权正定矩阵的联合。
根据二次型性能指标的线性系统最优控制理论,可以得到悬架系统的最优控制规律为
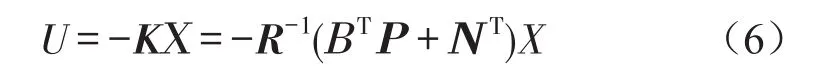
式中K——反馈增益矩阵。矩阵P由黎卡提方程求出
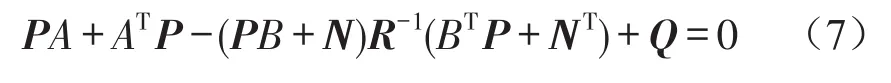
2.2人工群蜂优化算法
人工蜂群算法(ABC)[8]是模仿蜜蜂群体智能搜索的一种全局搜索能力很强,收敛速度快的优化算法,蜜蜂群体主要包括引领蜂、跟随蜂和侦察蜂组成。引领蜂的数量=跟随蜂的数量=优化问题中解的数量。整个过程就是引领蜂搜索含蜜量更多的食物源的过程。如果引领蜂搜索到新食物源中含蜜量多于之前搜索到的食物源时,就会用所得的新解来代替旧解;如果新解的适应度值比旧解的低的时候,则保持原来旧解的位置,即旧解的值不变。等所有的引领蜂搜索完后,它们会在舞蹈区通过摇摆舞蹈与跟随蜂共享食物源的位置和含蜜量等信息。交流完信息以后,跟随蜂会根据食物源收益率的大小来选择食物源,食物源的含蜜量越多就越容易被选中。等选中食物源以后,跟随蜂就会对食物源信息进行更新,它们会在现有食物源附近搜索新的食物源,以期获得含蜜量更高的食物源,即更优的解。这个过程经过不断的循环,解的质量也在不断地提高,最终获得最优解。具体操作流程如下
Step1:初始化种群,由式(8)得到初始解。
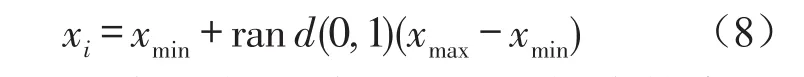
Step2:引领蜂按式(9)在可行解范围内搜索新解,计算新解的适应度值New fit(i),若New fit(i)>fit(i),则更新位置,否则失败次数lost(i)加1。
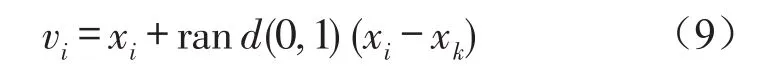
式中xmax和xmin为取值范围上限和下限值,New fit(i)为收索获得新食物源中含蜜量值,fit(i)为原食物源中含蜜量值。xk是随机取值。
计算每个个体的选择概率
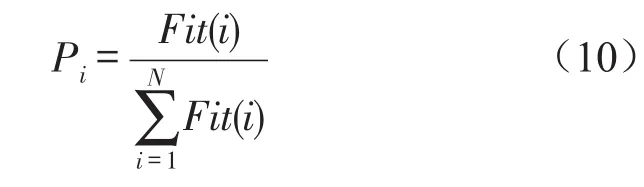
Step3:跟随蜂根据选择概率Pi在可行解范围内按式(9)搜索新解,若新解适应度值New fit(i)>fit(i),则更新位置,否则失败次数lost(i)加1。
Step4:若lost(i)>limit,则抛弃该解,引领蜂转变为侦察蜂,按式(8)搜索新解。
Step5:所得解的适应度若满足预先设定精度或达到最大迭代次数,则循环结束,输出最优解。流程图如图2所示。
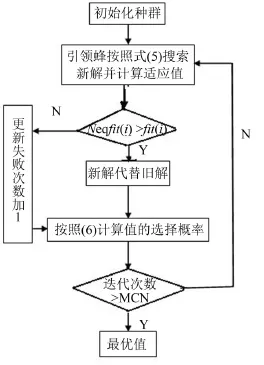
图2 人工群蜂算法流程图
2.3动态子群生成策略
在人工蜂群算法中,蜂群之间通过相互学习来寻找最优解,其主要是通过共享蜜蜂所发现最优解的过程,因此信息共享机制对算法的性能起关键作用,而蜂群之间的信息共享方式主要体现在蜂群的拓扑结构上,目前应用最广泛的拓扑结构有全互联拓扑结构和环形拓扑结构。全互联拓扑结构具有很强的交互性能和很大的交互开销,收敛速度较快,但容易陷入局部最优;环形拓扑结构中的蜜蜂只与自己相邻的蜜蜂交互,收敛速度较慢,但不易陷入局部最优。动态子群生成策略主要有理论全互联拓扑结构收敛速度较快和环形拓扑结构的不易陷入局部最优的优点,对蜂群进行动态子群生成策略,主要是将蜂群划分为确定规模的子群,在子群内部采用扩展的环形拓扑结构,进行蜂群信息共享,产生子群的最优解,按照式(11)进行搜索。
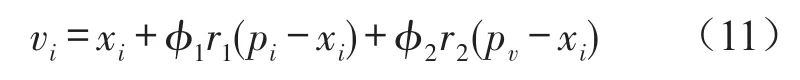
其中pν表示在迭代过程中,环形拓扑结构在蜜蜂i的邻居中蜜蜂所经历的最好位置。
然后以各子群的最优解组成上一层次的子群,采用全互联拓扑结构来实现该级子群的信息的共享,对其寻优,按照式(12)进行搜索。
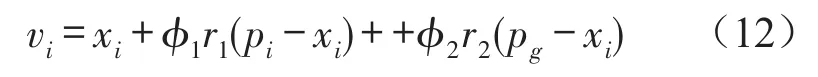
pg表示在迭代过程中,全互联拓扑结构中蜜蜂i的邻居中蜜蜂所经历的最好位置。
pi表示在迭代过程中,蜜蜂i所经历的最好位置,也称为“认知部分”学习。pν和pg称作粒子的“社会部分”学习。
该策略可以保证蜂群的多样性。子群之间的进化是并行的,每个子群只需通过环形拓扑结构来完成自己内部的进化,然后将其最优解向上层传递。上层子群主要是对下层子群的最优解采用全互联拓扑结构方式来指导各子群最优位置进化,引导下层粒子向着最优位置飞行。
2.4动态子群混合蜂群优化算法
人工蜂群算法结构简单、概念清晰,且容易实现全局优化性能好,但存在后期收敛速度慢、局部搜索能力弱等不足。为了提高人工蜂群算的性能,提出一种基于动态子群的混合蜂群优化算法。该方法是通过维划分形成子群,不同的子群采用不同的优化策略或优化技术对其进行优化,形成最优解,供下一个子群使用。该策略可有效地提高人工蜂群算法的性能[7-9]。
结合动态子群策略和蜂群优化算法的优点,建立一种基于动态子群的混合蜂群优化方法的悬架LQG控制器加权系数的优化算法,算法的基本思想是在人工蜂群算法的基础上,对蜂群进行子群动态划分形成不同结构的子群关系,并对不同的子群实行不同的优化策略或优化技术进行优化。可使蜂群获得最优解的过程,具体操作流程如下:
Step1:初始化种群,包括种群规模SN、蜜源个数N=(SN/2)、同一蜜源被限制次数Limit等参数,并随机初始化蜂群中各蜜蜂的位置Xi。按照优化函数评价群中所有蜜蜂f(Xi),将当前各蜜蜂的位置记为Pi=Xi;将所有蜜蜂中目标值f(Pi)最优的个体位置记为Pg。
Step2:将种群分为sp=N/n个子群,计算每个子群个体适应度值,引领蜂按照扩展的环形拓扑结构策略求子群j最优值pνj,并计算最优值的适应度值New fit(j),若New fit(j)>fit(j),则更新位置,否则失败次数lost(j)加1。
Step3:跟随蜂按照式(10)计算选择概率,选择蜜源,并由式(11)进行扩展的环形拓扑结构策略搜索以产生新解,计算新解的适应度值New fit(j),若新解适应度值New fit(j)>fit(j),则更新位置,否则失败次数lost(j)加1,按照Step2执行。
Step4:产生子群最优值集合pν,利用全互联拓扑策略进行搜索求种群全局最优pg。计算新解的适应度值New fit(j)若新解适应度值New fit(j)>fit(j),则更新位置,否则失败次数lost(j)加1。
Step5:跟随蜂按照式(10)计算选择概率,选择蜜源,并由式(12)进行扩展的全互联拓扑策略搜索以产生新解,计算新解的适应度值New fit(j),若新解适应度值New fit(i)>fit(i),则更新位置,否则失败次数lost(i)加1,按照Step4执行。
Step6:所得解的适应度若满足预先设定精度或达到最大迭代次数,若满足,则循环结束,输出最优解,或者返回Step2。
2.5优化模型
针对2自由度1/4车体模型车辆悬架LQG控制器各性能指标的权重系数进行优化,通过适当的优化算法求得最优解。优化数学模型主要包括设计变量和目标函数如下。
2.5.1优化变量
1/4车体模型车辆LQG控制器中包含的权重系数有轮胎动位移加权系数q1;悬架的动挠度加权系数q2;车身垂直加速度加权系数ρ1;悬架控制力加权系数ρ2。因此,优化过程的设计变量为
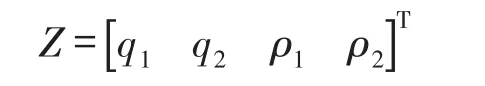
2.5.2目标函数
为了使控制器获得一个满意的控制效果,以被动悬架系统的性能的均方根作为参考,设定传统算法、人工蜂群算法和动态子群策略人工蜂群算法车辆主动悬架LQG控制的优化目标函数为

综合上述设计变量和目标函数,建立2自由度1/4车体模型车辆悬架LQG控制器性能指标权重系数的优化数学模型为
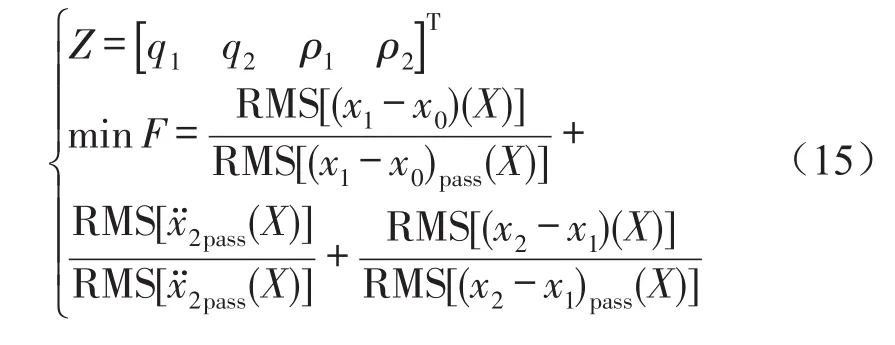
2.6路面输入模型
随机路面不平等度的产生方式通常有两种方法:一种是由白噪声——滤波器产生,另一种是由白噪声——积分器产生。本文采用后一种方法,即白噪声——积分器的生产方法模拟路面不平度。于是路面轮廓可由谱密度的白噪声——积分器产生,如式(16)所示[10]
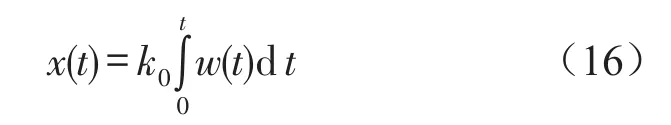
根据式(16),可在Matlab/Simulink中可建立路面输入模型,以C级路面行驶速度40 km/h作为仿真路况,仿真的路面模型如图3所示[10]。
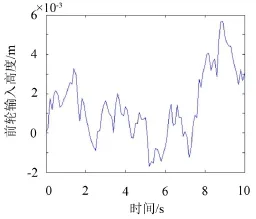
图3 路面仿真模型
3 控制策略仿真分析
取某车型参数为k0=138 000 N/m,
k1=20 600 N/m,c1=1 570 Ns/m,m0=20 kg,m1=430 kg q1,q2,的搜索范围为[1 106],ρ1的搜索范围为[110],ρ2的搜索范围为[01],SN取100,分别通过人工蜂群算法和动态子群策略人工蜂群算法优化得到的车辆悬架系统各个加权系数值。在相同结构参数和路面激励下
1)以积分白噪声模型作为地面输入分别对传统LQG控制器主动悬架、人工蜂群算法优化的主动悬架和利用动态子群人工蜂群算法优化的主动悬架进行了模型仿真。获得三种不同的仿真曲线,图4车体垂直加速度特性仿真,图5轮胎动位移特性仿真,图6悬架动挠度特性仿真。仿真结果,如表1所示。
从图4-图6可以看出,基于动态子群人工蜂群算法的LQG控制器显著降低了车体垂直加速度、轮胎动位和悬架动挠度。
2)以单位阶跃输入为路面输入模型,分别对传统LQG控制器主动悬架、人工蜂群算法优化的主动悬架和利用动态子群人工蜂群算法优化的主动悬架进行了模型仿真。获得三种不同的仿真曲线,图7车体垂直加速度特性仿真,图8轮胎动位移特性仿真,图9悬架动挠度特性仿真。
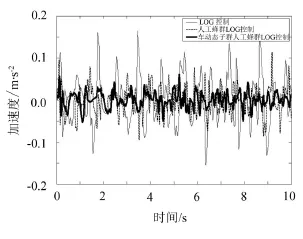
图4 车体垂直加速度特性仿真
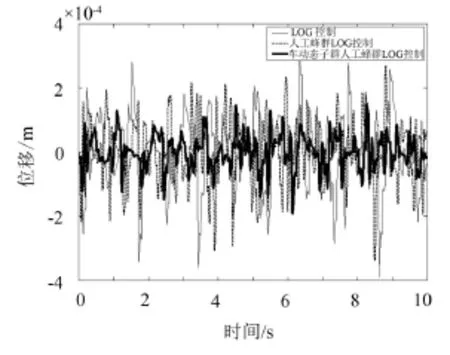
图5 轮胎动位移特性仿真
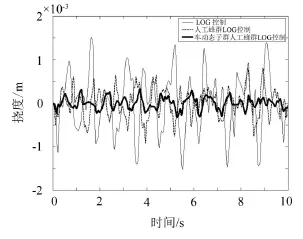
图6 悬架动挠度特性仿真
从图7-图9可以看出,基于动态子群人工蜂群算法的LQG控制器可较好地改善车体垂直加速度、轮胎动位和悬架动挠度的峰值和调整整时间。
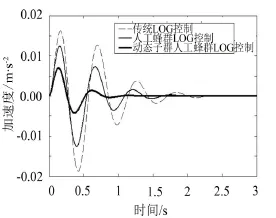
图7 车体垂直加速度特性仿真
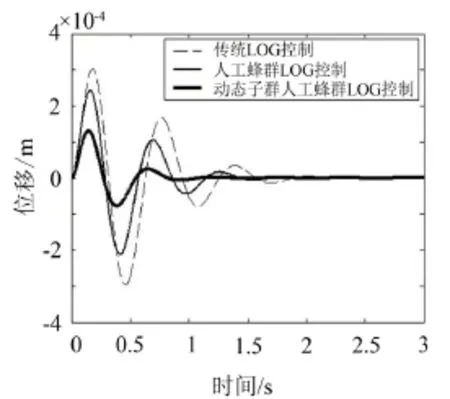
图8 轮胎动位移特性仿真
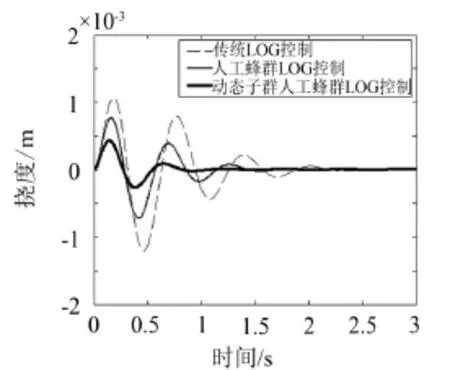
图9 悬架动挠度特性仿真
4 结语
利用动态子群策略局部搜索能力和人工蜂群算法全局搜索能力强的优点,对汽车悬架LQG最优控制算法中加权系数进行优化设计。提高汽车LQG控制器的设计效率和性能。通过对2自由度1/4车

表1 积分白噪声模型作为地面输入的性能指标
体汽车悬架模型仿真分析,通过对传统LQG控制方法、人工蜂群算法LQG控制方法和动态子群策略人工蜂群算法LQG控制方法进行仿真验证。
仿真结果表明,动态子群策略人工蜂群算法LQG控制方法相对于其它两种方法,在车体垂直加速度均方根、轮胎动位移均方根、悬架动挠度均方根方面都有明显减小;振动的幅度也有所减弱。对汽车的行驶平顺性和操纵稳定性有所改善。该方法的优化结果更接近最优解,为整车行驶平顺性和操纵稳定性的动态子群策略的人工蜂群最优控制应用奠定了基础。
[1]孟杰.基于遗传算法优化的汽车主动悬架LQG控制器的设计[J].机械科学与技术,2013(6):914-918.
[2]陈双.车辆主动悬架的遗传粒子群LQG控制方法[J].汽车工程,2015(2):189-193.
[3]桑楠.基于遗传算法的汽车主动悬架控制器优化设计[J].机械科学与技术,2013(9):1400-1404.
[4]李伟平.自适应模糊控制在磁流变半主动悬架中的应用[J].机械科学与技术,2013(9):1708-1713.
[5]张立军.参数灵敏度反馈车辆半主动悬架控制[J].噪声与振动控制,2015,35(5):72-134.
[6]张磊.车辆悬挂功率反馈主动控制算法[J].噪声与振动控制,2015,35(3):130-134.
[7]匡芳君.Tent混沌人工蜂群与粒子群混合算法[J].控制与决策,2015(5):839-847.
[8]代殿鑫.混合人工蜂群算法的改进硏究[D].广州:广东工业大学,2012.
[9]王伟.一种双层可变子群的动态粒子群优化算法[J].小型微型计算机系统,2012(1):145-150.
Design of the LQG Controller forAutomobileActive Suspensions based onArtificial Bee ColonyAlgorithm
ZHANG Hai-tao
(Department ofAutomobile Engineering,Anhui Technical College of Mechanical and Electrical Engineering,Wuhu 241002,Anhui China)
Based on LQG optimal control model of a 2-DOF quarter automobile suspension,an optimization method for determining the weighting factors combining local elitist strategy(LES)with artificial bee colony algorithm(ABC)is proposed.The LES has a strong local seeking ability while the ABC algorithm has a great global seeking ability.Simulation and comparative analysis on traditional LQG control,ABC LQG control and LES-ABC LQG control of the semi-active suspensions are conducted by means of Matlab/Simulink code.The models of integral white noise and unit step input are employed as the road input.Simulation results indicate that the LQG control method of LES-ABC algorithm can improve riding comfort and handle the performance of automobiles.
vibration and wave;LQG optimal control;optimization of weighting factors;dynamic sub-group strategy;artificial bee colony(ABC)algorithm;seeking ability
U463.33
ADOI编码:10.3969/j.issn.1006-1335.2016.05.014
1006-1355(2016)05-0065-05+81
2016-03-25
安徽省教育厅高校自然科学研究项目重点资助项目(KJ2016A138);院级青年教师发展支持计划科研资助项目(2015yjzr012)
张海涛,(1985-),男,安徽省皖寿县人,硕士研究生,讲师,主要研究方向为汽车系统动力学和计算机仿真。E-mail:zhanghaitao5238@163.com

