动车组车体截面轮廓对车体模态频率影响规律研究*

贾尚帅, 李明高, 张　军

(1　唐山轨道客车有限责任公司， 河北唐山 063035；2　大连交通大学载运工具先进技术研究中心， 辽宁大连 116028)



动车组车体截面轮廓对车体模态频率影响规律研究*

贾尚帅1, 李明高1, 张军2

(1唐山轨道客车有限责任公司， 河北唐山 063035；2大连交通大学载运工具先进技术研究中心， 辽宁大连 116028)

动车组车体结构模态是影响车辆乘坐舒适度的主要因素之一,车体结构模态须满足相关标准要求。建立某城际动车组车体参数化有限单元模型，计算车体模态，分析车体底架、侧墙、顶板总厚度及车体宽度、高度对车体模态的影响。通过车体截面轮廓参数对车体模态频率的影响规律分析对车体截面进行修改，得到理想的车体结构，提高车体模态频率使其满足相关标准要求。

动车组； 有限元法； 车体截面； 模态频率

车体是构成车辆的主体结构，对车辆的动力学性能有重要影响，车体结构模态是影响车辆乘坐舒适度的主要因素之一[1-4]。车体结构在减重的同时可能会使车体刚度相应降低，并导致车体模态频率不能满足相关要求；或者当车体结构设计不合理或材料选用不当时，也可能导致车体模态频率偏低，可能导致车体模态与转向架模态产生共振等问题，使车辆产生较大振动，因此车体模态频率要满足相关标准要求[5-6]。动车组车体普遍采用中空铝型材制造，由拉伸铝型材焊接形成车体底架、侧墙、顶板和端墙等主体结构，再将各结构焊接在一起形成车体。车体模态不但与构成车体底架、侧墙、顶板各板件的厚度及总厚度有关[7]，而且与车体高度和宽度关系密切[8]。

针对某城际动车组车体模态频率较低问题，建立车体有限单元模型，分析车体底架、侧墙、顶板总厚度及车体高度和宽度对车体模态频率的影响，得到较理性的车体结构，使车体模态频率得到较大提高。

1　结构模态分析基本理论

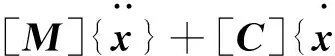
(1)

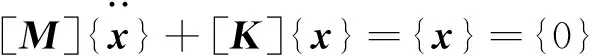
(2)

设{x}={X}eiωt，{X}为车体振动幅值向量，即车体振型向量，ω为车体自由振动角频率；代入式(2)，得车体振动的特征方程为

(3)

求解方程式(3)可以得到车体各阶模态频率λi(λi=ωi/2π)和振型{Xi}。车体前几阶模态对降低车体振动响应,提高乘坐舒适度是至关重要的。

2　车体有限单元模型及模态分析

2.1有限单元模型

该动车组为城际动车组，其特点为车体中间设置一个车门，加上车体两端的车门共3个车门，以方便旅客快速上、下车。车体用拉伸铝型材制造，铝型材的性能参数为：弹性模量为71 GPa，密度为2 700 kg/m3，泊松比为0.33。按照不同的结构部位及板壳厚度，整个车体共划分成96个组，每个组对应1个板壳厚度，板壳厚度从2.5 mm到15 mm不等。用Hypermesh软件划分车体有限单元网格，基于有限单元法用Nastran软件计算车体模态；车体共划分493 721个有限单元，采用三角形和四边形单元，以四边形单元为主，单元边长约为50 mm。总体和局部有限单元模型如图1所示。

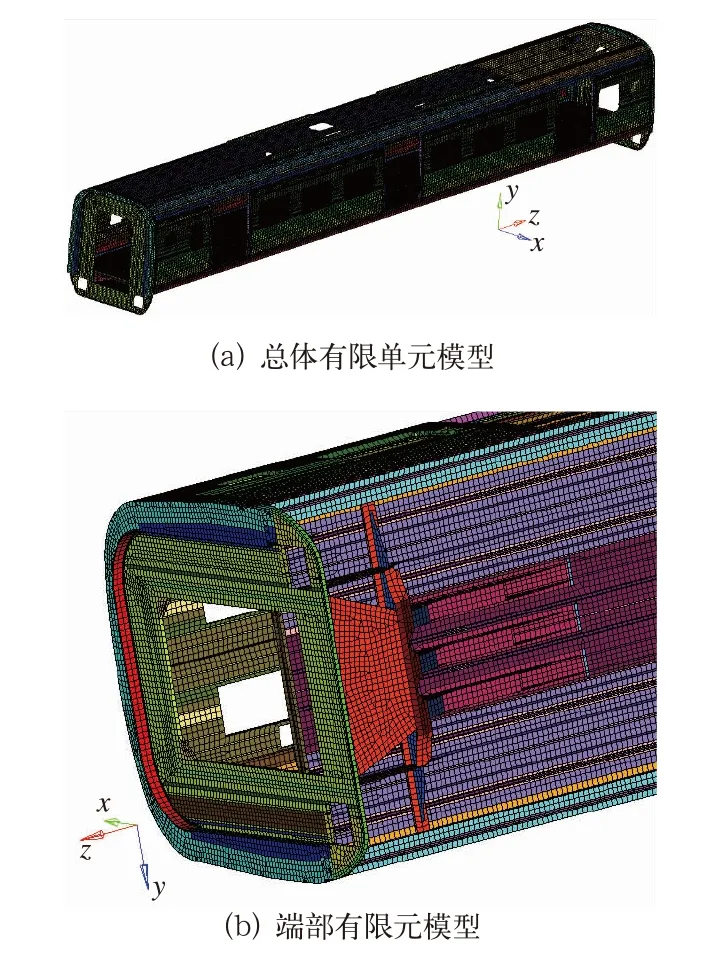
图1　车体有限单元模型

2.2模态计算

模态计算用整车模型，纯车体前3阶弯曲模态振型如图2所示，前3阶模态频率分别列在表1中。表1表明,该车铝合金车体一阶垂弯模态频率为14.85 Hz，该值较低，会降低车辆乘坐的舒适度，纯车体一阶垂弯模态频率一般需要大于17 Hz才能保整备车模态大于10 Hz的要求[9]，需要通过结构修改使其提高,以满足相关要求。

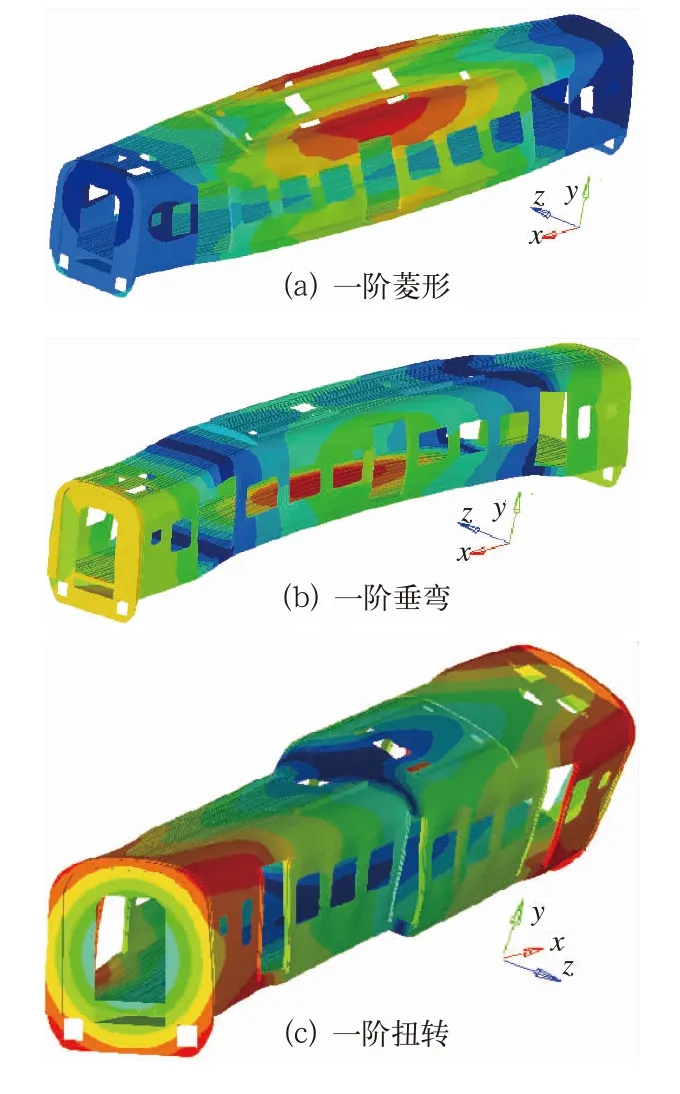
图2　车体前3阶模态振型

3　截面轮廓参数对模态频率的影响

3.1车体截面设计变量

车体截面轮廓参数如图3所示。主要计算车体截面主要轮廓参数对车体模态频率的影响，包括底架厚度、侧墙厚度、车顶厚度、车体高度、车体宽度5个参数。

表1　模态振型及频率

图3　车体截面轮廓参数

3.2截面参数对模态频率影响

车体底架厚度、侧墙厚度、车顶厚度、高度、宽度对车体前3阶模态频率的影响分别如表2～表6所示。各表中第一行为车体原始结构参数及模态频率值。

表2　底架厚度对模态频率影响

表2表明，底架厚度增加到74 mm时,车体1、2、3阶模态频率均有增加，其中1、2阶模态频率增加值大于3阶模态频率增加值；底架厚度增加到81 mm时，底架前3阶模态频率反而降低，可见从提高车体模态频率的角度来看，底架厚度有一个最佳厚度。

表3　侧墙厚度对模态频率影响

表3表明，侧墙厚度增加10%，其值增加到51 mm时，1阶模态频率得到提高，2阶模态频率保持不变，3阶模态频率略有降低；当侧墙厚度增加20%，其值增加到56 mm时，各阶模态频率均降低。

表4表明，车顶厚度增加10%，其值增加到53 mm时，1、2阶模态频率得到增加，3阶模态频率没有变化；车顶厚度增加20%，其值增加到58 mm时，1阶模态频率降低，但高于原始值，2阶模态频率保持不变，3阶模态频率略有降低。

表4　车顶厚度对模态频率影响

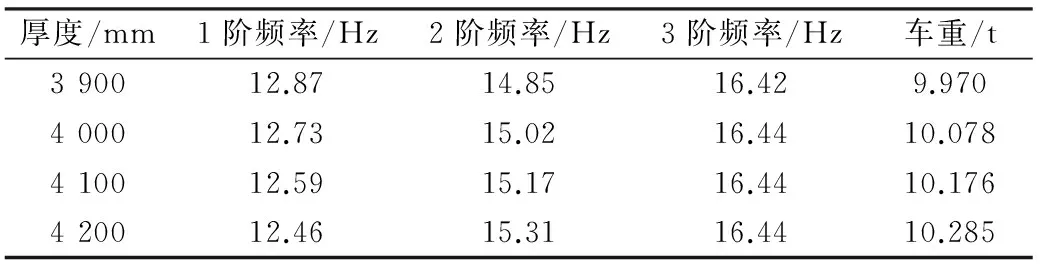
表5　车体高度对模态频率影响

车体高度是从轨道表面到车顶最高点的高度，车体高度增加时保持其他参数不变，包括底架厚度、车顶和侧墙厚度都保持不变。表5表明，随着车体高度增加，1阶模态频率逐渐降低，每100 mm大约降低0.14 Hz；2阶模态频率逐渐增加，3阶模态频率基本保持不变。

表6　车体宽度对模态频率影响

表6表明，随着车体宽度的增加，车体1、2、3阶模态频率均逐渐降低。

3.3改进后车体模态分析

以上分析表明，增加车体高度、减小车体宽度可以明显提高车体一阶垂弯模态频率，车体底架厚度增加10%也可以提高车体一阶垂弯模态频率，侧墙、车顶厚度增加对提高一阶垂弯模态频率效果一般。基于以上规律分析，底架厚度增加到74 mm，车体宽度减小到3 176 mm，车体高度增加到4 200 mm，此时车体质量为10.123 t，比原结构增加了0.153 t，但车体一阶垂弯模态频率增加到15.61 Hz，明显的提高了车体一阶垂弯频率的效果。在修改车体截面参数的基础上，通过板件厚度优化，在保证车体质量没有较大增加的基础上，使车体第2阶模态既一阶垂弯模态频率提高到了17 Hz。

4　结　论

本文建立了某城际动车组铝合金车体车参数化有限单元模型，计算了车体模态，分析了车体前3阶模态频率随底架厚度、侧墙厚度、车顶厚度、车体高度、车体宽度的变化规律。分析表明，底架厚度改变对车体模态频率的影响大于车体侧墙、车顶厚度改变的影响，底架厚度有一个最佳的厚度值使车体一阶垂弯模态频率最大；对于分析的3门车体来说，侧墙厚度增加使第3阶模态(一阶扭转)态频率降低，第1阶模态(一阶菱形)频率增加，对第2阶(一阶垂弯)模态频率影响较小；车顶厚度增加使第1、2阶模态频率略为增加，对第3阶模态频率影响较小。车体高度增加，使第2阶模态(一阶垂弯)频率增加明显，但会导致1阶模态(一阶菱形)频率降低，对车体第3阶模态(一阶扭转)模态频率影响较小；随着车体宽度的增加，车体第1阶(一阶菱形)、第2阶(一阶垂弯)、第3阶(一阶扭转)模态频率均逐渐降低。通过计算分析，合理修改车体截面结构参数使车体第2阶模态(一阶垂弯)频率提高到了 15.61 Hz，在此基础上通过对车体板壳厚度优化使车体一阶垂弯模态频率提高到了17 Hz，达到了预期效果。

[1]吴丹,商跃进,王红，等. 160 km/h轨道车车体模态和稳定性有限元分析[J]. 机车电传动, 2011,(5): 14-16.

[2]平学成,王先亮,朱韶光， 等. B型地铁铝合金车体工作模态分析[J].铁道机车车辆, 2015, 35(1): 115-117.

[3]宫岛,周劲松,孙文静， 等. 铁道车辆弹性车体垂向运行平稳性最优控制[J]. 同济大学学报, 2011, 39(3):416-420.

[4]罗光兵,曾京. 基于弹性结构的轨道车辆振动分析[J]. 机械设计与制造,2013,5:67-73.

[5]赵阳阳,刘士煜. 高速列车承载结构模态频率提高策略研究[J]. 佳木斯大学学报,2011,29(4): 496-499.

[6]沈宏峻，周劲松，等． 铰接式客车车体的轻量化 设计和模态分析[J]．铁道学报,1997,(19):46-51．

[7]干宇文,张立民. 高速列车承载结构对车体模态频率的影响[J].机械,2013,40(11):26-28.

[8]佟维, 刘晓雪. 高速动车组铝合金车体结构优化策略[J].计算力学学报，2009，26(3):424-427.

[9]张远亮，张立民，张艳斌.车体配重对车体1阶垂弯频率的影响分析[J].铁道机车车辆, 2015, 35(1): 51-53.

Modal Frequency Rule with the Section Parameters of EMU Bodywork

JIAShangshuai1,LIMinggao1,ZHANGJun2

(1Tangshan Railway Vehicle Co., Ltd., Tangshan 063035 Hebei, China;2College of Traffic and Transportation Engineering, Dalian Jiaotong University, Dalian 116028 Liaoning, China)

The bodywork modal frequencies have the significant effect on carborne, the modal frequencies of carbody should meet the standard request. A finite element model of EMU bodywork is established, the bodywork modals are calculated, and the change rules of modal frequencies with the bottom thicknesses, the side wall thicknesses, top plate thicknesses, vehicle heights and vehicle widths are analyzed and generalized. Basing on the change rules of modal frequencies, the section parameters are revamped, the modal frequencies of bodywork are increased, the relative standards that the frequency of first order bending mode is satisfied.

EMU； finite element method； bodywork section； modal frequency

1008-7842 (2016) 03-0043-03

��)男，工程师(

2015-12-30)

U266.32

Adoi:10.3969/j.issn.1008-7842.2016.03.09

*中国铁道总公司项目资助(2014J004-O)；牵引动力国家重点实验室开放课题资助(TPL1402)