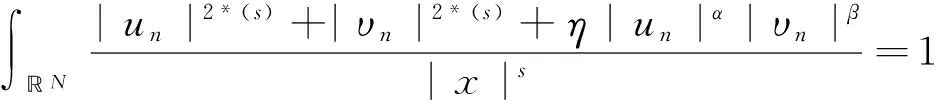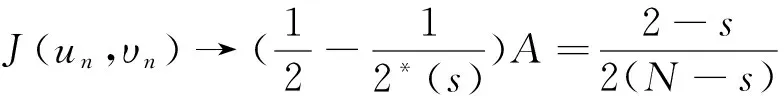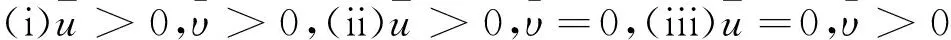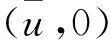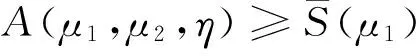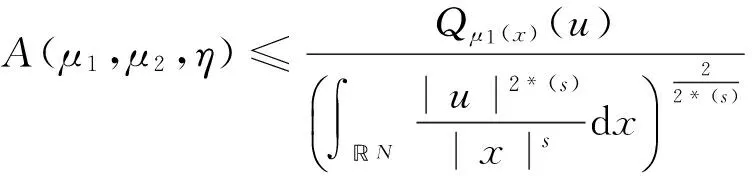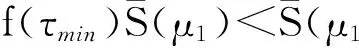全空间中带有不同Hardy项的临界椭圆方程组的基态解
康东升,段 笑, 龚睫茜
(中南民族大学 数学与统计学学院,武汉 430074)
全空间中带有不同Hardy项的临界椭圆方程组的基态解
康东升,段笑, 龚睫茜
(中南民族大学 数学与统计学学院,武汉 430074)
研究了带有不同Hardy项的非线性临界椭圆方程组以及与Rayleigh商相关的极小值问题,运用变分原理和分析技巧,证明了Hardy项系数分别为常系数和变系数时方程组正基态解的存在性.
椭圆方程组;基态解;变分法;Rayleigh商
1 本文的主要结果
本文首先研究以下带有不同Hardy项和多重Hardy-Sobolev临界项的椭圆方程组:
其中D:=D1,2(N)是(N)关于(∫|的完备化空间,是最佳Hardy常数,是Hardy-Sobolev临界指数.
当方程组中的μ1,μ2和η取常数时,满足如下假设:
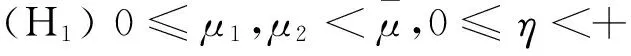
(H2) N≥3,0
更一般地,当方程组的μ1,μ2和η为变系数时,方程组除了满足(H2)以外,变系数还满足以下条件:
(H3) η(x)∈C(N,),η(x)≥0,存在极限,并且:
(H4) μ1(x),μ2(x)∈C(N,),μ1(0)≥μ2(0)≥0,存在极限,并且满足:

(H5) 以下不等式至少有一个成立:

为方便起见,在本文中有时省略掉积分号里面的dx.方程组(1)与以下的Hardy-Sobolev不等式相关[1]:
特别地,当s=2时得到如下重要的Hardy不等式[2]:

根据Hardy不等式,可以定义空间D:=D1,2(N)和D2:=D×D上的等价范数:
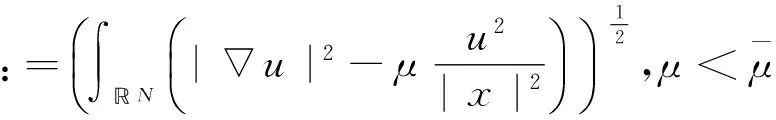
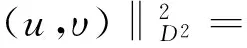
方程组(1)的常系数形式对应的能量泛函为:


则I∈C1(D2,),在D2与其对偶空间(D2)-1之间,可以定义对偶积I′(u,υ),(φ,φ),其中(u,υ),(φ,φ)∈D2,I′(u,υ)是I的Frechet导数.
当(H1)~(H5)成立时,可以定义如下最佳常数[3,4]:
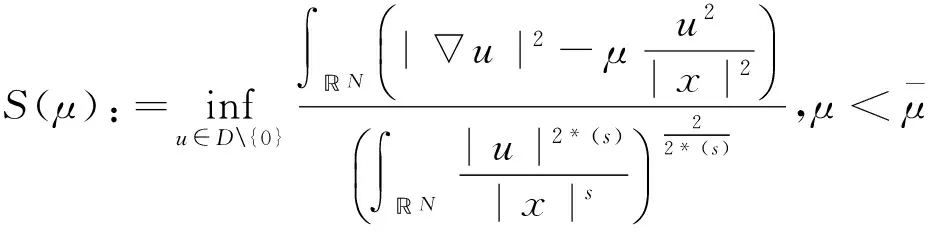

i=1,2.
(2)
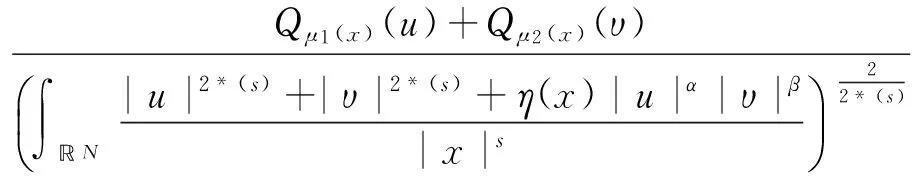
(3)
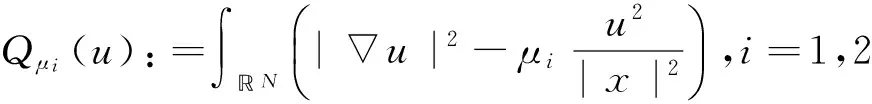



当μ1,μ2,η为常数时,将上述最佳常数A改写为B:

(4)
在(H1),(H2)成立的情况下,∀τ≥0,定义如下函数和记号:
(5)
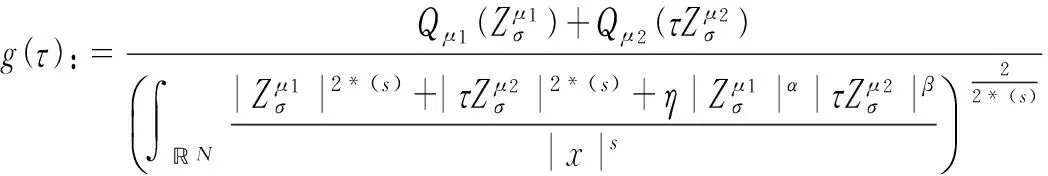
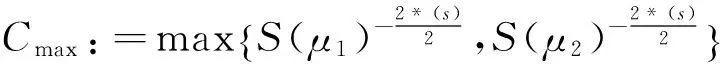
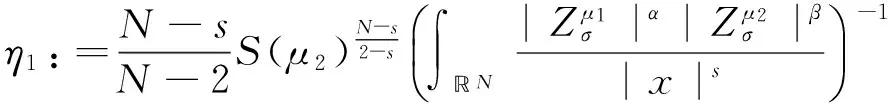

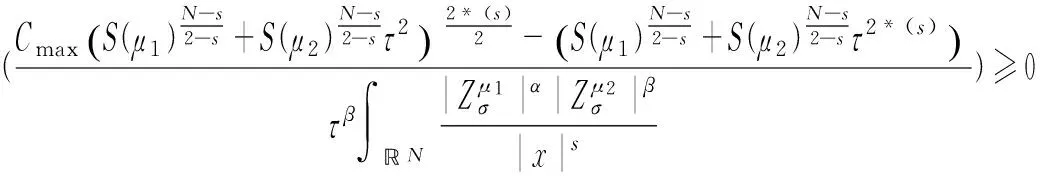
另外,定义以下集合(Nehari流形)和记号:
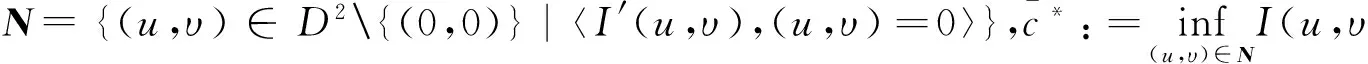
通过简单的证明可以得到:

本文的主要结果是下面的两个定理.
定理1假设(H1),(H2)成立,并且下列条件有一个是满足的:
(i) α<2,β<2,η>0.
(ii) α<2,β=2,η>η1.
(iii) α=2,β<2,η>η2.
(iv) α=β=2,η>max{η1,η2}.
(v) η>η3.
则B(μ1,μ2,η) 把常系数方程组的上述结论运用到变系数方程组,可以得到变系数方程组正基态解的存在性.为方便讨论,先针对方程组的变系数形式给出以下定义: 定理2假设(H2)~(H5)成立,且以下条件有一个满足: (i) α<2,β<2,η>0. 首先,对于变系数方程组,在D×D上定义如下泛函: J(u,υ):= 则J∈C1(D2,). 如果(u,υ)∈D2为J的非零临界点,则为非平凡解. 引理1若(H2)~(H4)成立,则对于任意的c (6) 证明证明与文献[4]中引理2.1类似,这里只对部分不同点作出说明,不作详细论证. (7) (8) (9) 其中δx是在点x的Dirac质量.根据上述(7)~(9)式,应用文献[4]的推理,我们可以得到: (10) (11) 另一方面, c=J(un,υn)- 由(H2)~(H4),(6),(10), (11)式可得: 所以子序列(un,υn)在D2中强收敛于(u,υ), 引理1得证. 证明此引理的证明与文献[8]的引理2.1基本相同,这里略去详细过程. 引理3 若假设(H2)~(H4)成立,且以下条件有一个满足: (i) β<2,η>0, 证明根据文献[9]中定理1.1的证明,可以得到: 由f(τ)的定义式(5),对f(τ)求导可得: 若条件(iii)成立,即: B(μ1,μ2,η)≤g(τ),τ≥0. B(μ1,μ2,η)≤ min{g(0),g(∞)}=min{S(μ1),S(μ2)}. 在[0,∞)上考虑以下函数 直接对g(τ)进行求导计算可知,若定理1中条件(i)~(iv)有一个成立,则当τ→0+时g′(τ)<0,当τ→+∞时g′(τ)>0,因此就有: ming(τ)< min{g(0),g(∞)}=min{S(μ1),S(μ2)}. 所以g(τ)存在一个最小值点τ1∈(0,∞),使得: B(μ1,μ2,η)≤ g(τ1)=ming(τ) (12) 若η>η3,则由η3的定义可知,存在τ2∈(0,∞),使得: min{S(μ1),S(μ2)}=min{g(0),g(∞)}, 所以(12)式同样成立.则由引理2可知,定理1成立. 定理2的证明由(H2)~(H5)可知: (13) 同时,若定理2的条件成立,引理3的条件也是满足的,故引理3同样成立. 注意到Q(u,υ)=Qμ1(u)+Qμ2(υ)是正定的,并且在D2上提供了一种等价范数.设{(un,υn)}为A的极小化序列,根据商的齐次性,可以假设: 根据Ekeland变分原理,对任意(φ,φ)∈D×D,我们假设{(un,υn)}有Palais-Smale性质: o(‖(φ,φ)‖D×D)=J′(un,υn),(φ,φ). 由(13)式可得: (14) (15) 对任意u∈D{0},将(u,0)代入(3)式可得: ∀u∈D{0}, 故由(2)式可得: (16) 根据(15)和(16)式可以得到: (17) 于是A(μ1,μ2,η)的值只依赖于μ1而与μ2,η无关.由(17)式和引理3可以得到: [1]Cafarelli L, Kohn R, Nirenberg L. First order interpolation inequality with weights[J]. Compos Math, 1984, 53(1): 259-275. [2]Hardy G, Littlewood J, Polya G. Inequalities[M]. Cambridge: Cambridge University Press, 1988: 239-243. [3]Kang D, Peng S. Positive solutions for singular critical elliptic problems[J]. Applied Math Lett, 2004,17:411-416. [4]Kang D. Systems of elliptic equations involving multiple critical nonlinearities and different Hardy-type terms inN[J]. J Math Anal Appl, 2014, 420(2): 917-929. [5]Lions P L. The concentration compactness principle in the calculus of variations, the limit case(I)[J]. Rev Mat Iberoamericana, 1985, 1(1): 145-201. [6]Lions P L. The concentration compactness principle in the calculus of variations, the limit case(II)[J]. Rev Mat Iberoamericana, 1985, 1(2): 45-121. [7]Kang D. Concentration compactness principles for the systems of elliptic equations[J].Differ Equ Appl, 2012, 4(2): 435-444. [8]Kang D, Yu J. Minimizers to Rayleigh quotients of critical elliptic systems involving different Hardy-type terms[J]. Appl Math Lett, 2016, 57: 97-103. [9]Huang Y, Kang D. On the singular elliptic systems involving multiple critical Sobolev exponents[J]. Nonlinear Anal, 2011, 74(2): 400-412. [10]Vazquez J. A strong maximum principle for some quasilinear elliptic equations[J].Appl Math Optimt, 1984,12(2): 191-202. Ground State Solution to Critical Elliptic Systems Involving Different Hardy-Type Terms in the Whole Space KangDongsheng,DuanXiao,GongJiexi (College of Mathematics and Statistics,South-Central University for Nationalities,Wuhan 430074, China) In this paper, nonlinear critical elliptic systems involving different Hardy-type terms were investigated and the minimizers to Rayleigh quotients were studied. By variational methods and analytical techniques, the existence of positive ground state solutions to the systems was verified,where the coefficients of Hardy-type terms are constants and functions respectively. elliptic system; ground state solution; variational method; Rayleigh quotient 2016-05-27 康东升(1967-),男,教授,博士,研究方向:偏微分方程,E-mail: dongshengkang@scuec.edu.cn 国家自然科学基金资助项目(11601530) O175.25 A 1672-4321(2016)03-0141-03



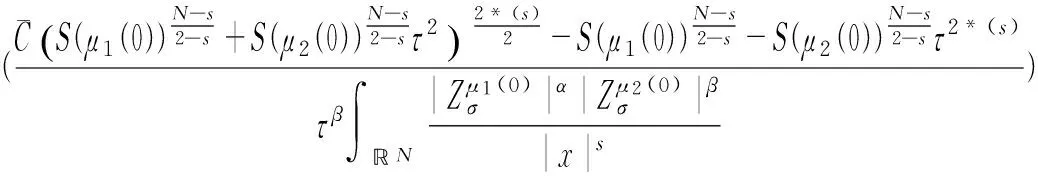
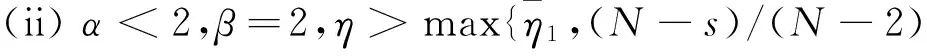
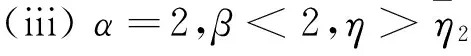



2 预备引理
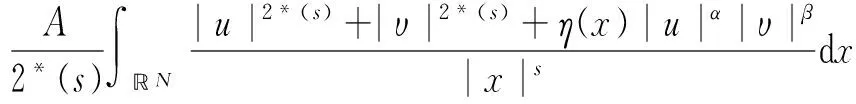

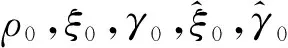
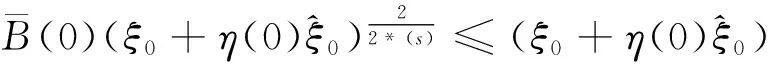

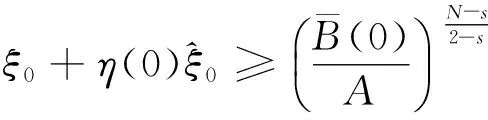

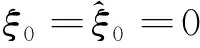

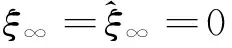
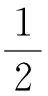


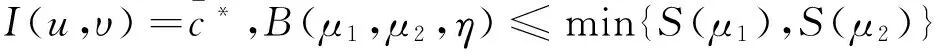
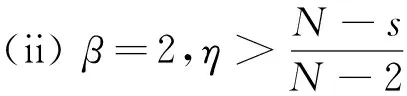
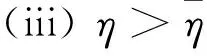
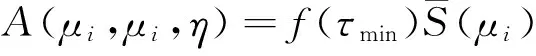



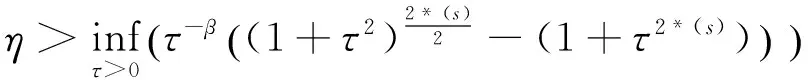
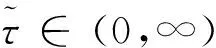
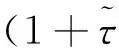
3 定理的证明