基于节点标号的Koch网络结构性质研究

翟因虎，王银河

(广东工业大学 a.自动化学院，b.信息工程学院，广州 510006)



基于节点标号的Koch网络结构性质研究

翟因虎a,b，王银河a

(广东工业大学 a.自动化学院，b.信息工程学院，广州 510006)

针对正多边形Koch分形岛所映射成的Koch网络，根据节点接入网络的时间和位置信息给节点标号。在节点标号的基础上，研究网络的最短路由及计算最短路径长度；并分析网络的主要结构性质，如节点的度、度分布和累积度分布函数，以及网络的聚类系数、平均最短路径长度、度关联函数和介数中心性，得出结构性质的解析解。结果表明，所构建的Koch网络是无标度和小世界的；其聚类系数趋向于比较大的常数值；平均路径长度与网络节点数的对数呈正比关系，度相关函数、点介数和边介数都随节点度的变化而指数变化。

Koch网络；节点标号；网络性质；最短路由

0　引言

如何适当地构建网络模型是复杂网络研究中最根本问题之一，因为复杂网络的拓扑结构与网络的动力学行为和功能是密切相关相互影响的。我们生活中存在各种复杂的社会和技术网络，如社交网络、科研合作网络、交通网络、疾病传播网络、基因调控网络、细胞代谢网络、食物链网络、脑神经网络和生态网络等，为了深入研究和理解这些网络，必须构造与实际网络拓扑结构本质相似或同构的网络模型。Watts和Strogatz在1998年提出了小世界网络WS模型[1]，它具有较小最短路径和较大集聚系数，成功解释了社会学的“六度分离”现象；Barabasi和Albert在1999年提出了无标度网络BA模型[2]，它具有幂律度分布，符合大多数复杂网络的基本特性，从而与Watts等共同开创了复杂网络研究的先河。自此之后，关于复杂网络及其模型的研究就如雨后春笋般蓬勃发展。由于BA无标度网络模型和WS小世界网络模型与许多现实网络特性存在一些偏离，很多研究人员提出了多种推广的随机模型，使得这些随机模型生成的网络更接近现实。但是，上述随机模型模拟实际网络时存在一些问题，比如随机加边或随机重连等网络生成机制与实际网络的演化过程不相符，所生成的网络模型不直观，网络结构性质的分析必须使用统计物理等高深的理论工具且对节点数目巨大的网络计算量灾难性增加，关于网络功能和动力学的结论难于定性定量分析等。

而以确定性方式生成的网络，不但形象直观，而且使人更容易了解网络的生成特点以及节点间的相互作用关系，更重要的是，容易得到复杂网络结构性质、功能和动力学的精确解析解，对复杂网络的深入研究具有特殊的价值和意义。循着这个思路，2000年以来，具有不同性质的确定性网络模型逐渐被提出和研究[3]。比如第一个小世界网络确定性模型被Comellas等提出[4]。确定性均匀递归树是最简单的确定性模型之一，累积度分布以指数形式衰减，平均路径长度随着网络的规模呈现对数形式增长，为正相关的小世界网络，节点介数服从指数为2的幂律分布，特别是邻接矩阵的所有特征值互不相同，这一性质是独一无二的，是目前其它的网络所不具备的[3,5]。第一个层次网络确定性模型被Barabasi等提出和研究[6]，该网络是无标度的、幂律指数为2；这类网络模型节点度服从幂律分布，节点的集聚系数与其度成反比，层次网络模型为人们研究复杂网络提供了新的视角和方法，该确定性层次网络发表后不久，便引起了广泛关注。周涛等[7]研究了整数网络，发现其聚类系数趋于0.34且出度服从幂率分布。方锦清等[8]研究了Farey有理数树状网络，证明网络度分布服从指数分布。

复杂性问题的研究方法总结起来主要有：分子动力学、混沌、分形、复杂网络等。于是自然有人要问：这些复杂性问题的研究方法之间有什么联系呢？由经典分形(如Apollo分形垫、Sierpinski分形垫、Koch曲线)映射为复杂网络，可以把复杂性问题的两大重要分支——分形和复杂网络联系起来[3]。Apollo分形垫映射成的复杂网络得到了广泛的研究，这是一种无标度小世界网络，聚类系数高达0.828，幂指数为2.85[9-10]。Sierpinski分形垫映射成的复杂网络是最大可平面图，幂率指数为2+ln3/ln2，聚类系数趋于0.598的小世界网络[11-12]。章忠志等还对诸多分形映射成确定性模型的结构性质、功能和动力学过程进行了开创性的研究[12-21]，这些分形网络都为小世界、无标度网络，具有较高的聚类系数，适合作为实证网络的研究模型。

Koch网络是根据经典的Koch分形曲线构造的，该网络的性质与许多真实世界网络相似，同时具有无标度、小世界和高聚类系数等实际网络的特性，有着重要的研究价值[17-21]。章忠志等研究了平面Koch网络的构造与结构性质的分析、Laplace谱的分析解和网络中的随机游走，结果表明网络是无标度的、度分布临界指数范围为[2，3]，聚类系数大概为0.9左右，度相关近似为指数为负数的幂率分布，并分析了这类网络的随机游走动力学过程[17-21]。鉴于Koch网络的重要作用，不少作者对Koch网络进行了诸多有益的拓展研究，主要体现在构造机理不变，把三角形基本单元变换为其它不同种类的结构单元。刘甲雪等研究了以四面体为基本单元的立体Koch网络[22]，发现聚类系数趋于0.870 435，平均路径长度的增长行为同平面Koch 网络的十分近似，但是其度分布临界指数γ>3，立体Koch 网络具有度关联性，但是不能构建任意的无度关联性的无标度网络。傅新楚等研究了正八面体Koch网络的结构性质[23]，发现这种网络是无标度的、且度分布临界指数γ>3，是一种聚类系数趋于0.68的同配网络，投影在平面上时构成一种特殊的最近邻耦合Koch网络。孙伟刚等研究了正多边形Koch网络的结构性质和随机游走，网络是无标度的、且度分布临界指数为γ=ln(m+1)/ln2+1，其中m为正整数；当m>3时聚类系数为0，当m=3就是平面Koch网络[24-25]。孙伟刚等还研究了正多面体Koch网络，网络是无标度的、度分布临界指数范围为[2，3]，与平面Koch网络相同；具有很高的聚类系数；平均路径长度与网络大小对数成正比，是一种异配网络[26]。张红娟等把边权导入了多边形Koch网络，构成了有权网络，并对其上的随机游动进行了研究[27]。

网络或者图的标号问题的背景主要来源于实际问题，到目前为止已有十几种标号被定义，其应用范围已深入到诸如码论、X-射线结晶学、天文学、雷达和循环设计等领域。 关于图标号问题，早期主要研究某种特殊图是否具有某种标号，如优美标号和协调标号。这些标号都是不含节点拓扑关系等信息的标号方法。最近的研究表明，为了深入分析复杂网络确定性模型的结构性质、最短路由和随机游走等动力学过程，可以采用包含节点间拓扑关系信息的标号方法来标记网络节点，如阿波罗网络[28]、自相似外可平面无聚类图[29]和无标度模块化可平面图[30]等确定性模型。在包含相关信息的节点标号帮助下，以上作者成功地获得复杂网络确定性模型的性质或者最短路由。受上文启发，我们给平面Koch网络找到了一种包含节点接入网络时间和位置信息的标号方法,以便更加深入地研究Koch网络的不容易用迭代方法推导得到的重要性质。

目前，关于Koch网络的研究更多的偏重于拓展网络构成基本单元的类别，而关于一些Koch网络的深入研究，比如正多边形Koch分形岛映射成的复杂Koch网络的主要结构性质、Koch网络的节点标号方法、最短路由、最短路径长度、节点和边介数的计算，还没有文章见诸报端。本文研究正多边形Koch分形岛映射成Koch演化网络，给出一种有效的节点标号方法，并基于此节点标号分析了Koch网络的主要拓扑性质、最短路由、最短路径长度和网络节点与边的介数的解析解。基于本文结论，可有助于更加深入地定性定量研究上述Koch网络的多种重要性质，还可以有助于深入研究复杂网络随机模型和实证网络的结构、功能和动力学过程。

1　Koch网络模型

Koch分形岛的生成方式为：1)当迭代次数t=0时，分形岛为正n边形，即启动子为正n边形(其中n∈Ø+)； 2)t每次增加1时，分形岛的每条直线段都均匀分割为2m+1(其中m∈Ø+)整数段并依次编号，再把标号为偶数的直线段替换为等边三角形，然后去掉此标号为偶数的直线段，也就是生成子为上述迭代方式；3)如此迭代t次，即得到Koch分形岛S(n,m,t)。显然，单独一条直线段生成的分形为基本分形S(1,m,t)，且分形岛S(n,m,t)为n个基本分形S(1,m,t)依次相连而成。图1外圈所示的图形为Koch分形岛S(6,2,2)，其中红色线段对应t=0，黑色线段对应t=1，蓝色线段对应t=2。

把上述Koch分形岛S(n,m,ti)(ti=0,1,2,…,t)中的直线段映射为网络节点，把两直线段之间的连接关系映射为相应两节点之间的连边，就可以得到Koch网络K(n,m,t)。一条直线上生成的分形S(1,m,t)映射成子网络K(1,m,t)，n个子网络K(1,m,t)的Hub节点依次相连就构成Koch网络K(n,m,t)。图1内圈所示的图形为网络K(6,2,2)，其中红色节点为t=0时红色线段映射而成，黑色节点为t=1时黑色线段映射而成，蓝色节点为t=2时蓝色线段映射而成，直线段之间的相交对应相应节点间的连线。图1中网络K(6,2,2)由6个相同的子网络K(1,2,2)组成。可见，为了研究网络K(n,m,t)，必须先研究子网络K(1,m,t)。

2　Koch网络的节点标号与最短路由

2.1网络的节点标号

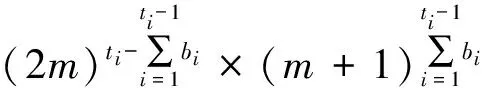
2.2网络的最短路由

定义M(i)为i时刻接入网络节点的标号集合，显然M(0)={1,2,…,n}且M(i)={gb1b2b3…bi.l(i)}。

定义L(n,m,t)为网络K(n,m,t)中所有节点标号的集合，则有

(1)

令L(v)为节点v的邻居节点标号集， Le(v)，Ll(v) 和 Lh(v)分别为与节点v的度相等、小于和大于关系的邻居节点的标号集合。显然

L(v)=Ll(v)∪Lh(v)∪Le(v)

(2)

其中

Ll(v)={gb1b2…bi0.lv(i+1),gb1b2…bi01.lv(i+2),

…,gb1b2…bi01…1.lv(t)}

(3)

(4)

Le(v)={gb1b2b3…bi.le(i)}

(5)

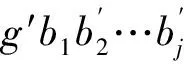
3　Koch网络的结构性质

根据Koch网络的构造机制，可得K(1,m,t)的节点总数和边总数分别为

N(1,m,t)=2×((3m+1)t-1)/3+1

(6)

E(1,m,t)=(3m+1)t-1

(7)

若节点v在ti时刻加入网络，在t时刻的节点度为

k=kv(1,m,ti)=2×(m+1)t-ti

(8)

其中，当ti=0时，kv(1,m,0)=2(m+1)t-2。每步迭代后K(1,m,t)节点数目的增量，即K(1,m,t)中与节点v度相同的节点数目为Lv(1,m,ti)=2m×(3m+1)ti-1，则K(1,m,t)的度平均为

(9)

可见子网络K(1,m,t)具有稀疏的网络结构，符合真实网络的特点。

网络K(n,m,t)的节点与边总数为

N(n,m,t)=n×(2×(3m+1)t+1)/3

(10)

E(n,m,t)=n×m×(3m+1)t-1

(11)

网络K(n,m,t)中ti时刻加入网络的节点v在t时刻的度为k=kv(n,m,ti)=2(m+1)t-ti，与式(9)相同，网络中度相等节点的数目为Lv(n,m,ti)=2nm×(3m+1)ti-1，且Lv(n,m,0)=n，则 K(n,m,t)的度平均〈k〉为

(12)

可见网络K(n,m,t)是与网络K(1,m,t)一样的稀疏网络，度平均都是基本相同的。

3.1度分布

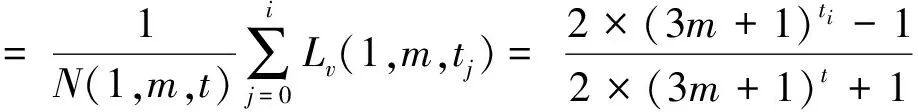
(13)

(14)

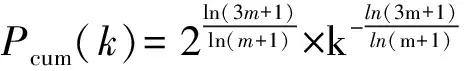
3.2聚类系数

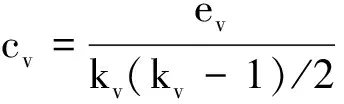
(15)

图3a为子网络K(1,m,t)的聚类系数图，其中m和t的取值范围都为1到20。由图可见，子网络K(1,m,t)具有很高的聚类系数，比如当m=1时，聚类系数趋于0.820 1。m越大，聚类系数越高； t越大，聚类系数也越高； 聚类系数随着m和t的增加而趋于常数。因为网络K(1,1,1)为一个三角形，此时网络聚类系数为1，所以图3a在t=1，m=1存在一个尖峰。

C(n,m,t)=

(16a)

当n>3时，

(16b)

C(n,m,t)如图3b所示，可见网络K(n,m,t)与子网络K(1,m,t)一样，都具有很高的聚类系数，并随着m和t的增加而趋于常数。

3.3平均最短路径长度

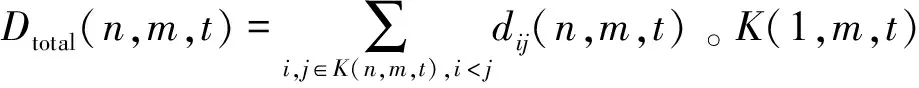
(17)

为了求出Dtotal(1,m,t)，必须先研究如图4a所示的网络K(1,m,t+1)构成图。网络K(1,m,t+1)中，在节点X处共有m+1个子网络Ki(1,m,t)(i=1,2,…,m+1)相互连接(注意节点X同时属于上述m+1个子网络)；在节点Y1到Y2m处，分别连接子网络Ki(1,m,t)(i=m+2, m+3,…,3m+1)(注意Yi点属于子网络Ki+1+m(1,m,t), i=1,2,…,2m)。由于节点X是重合点，可得K(1,m,t+1)与任意子网络Ki(1,m,t)所有节点最短路径和的关系

Dtotal(1,m,t+1)=

(3m+1)×Dtotal(1,m,t)+

Ω(1,m,t)

(18)

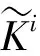
Ω(1,m,t)=(3m2+m)×s(1,m,t)×(3×N(1,m,t)-1)-2m2×N(1,m,t)+

(6m2-m)×N2(1,m,t)

(19)

由图4a易知s(1,m,t+1)=(m+1)×s(1,m,t)+2m×(s(1,m,t)+N(1,m,t)-1)+2m，且s(1,m,2)=2m×(5m+2)，所以可以解出

s(1,m,t)=((12mt+6m+2)×(3m+1)t-1-2)/9

(20)

把式(6)和(20)代入式(19)得

(21)

又因为由式(18)可以得到

(22)

且Dtotal(1,m,1)=4m2-m，再把式(21)代入(22)可以解出

(23)

所以，

(24)

网络K(n,m,t)的平均路径长度为

d(n,m,t)=

(25)

又由图4b所示K(n,m,t)的结构示意图，可得

Dtotal(n,m,t)=n×Dtotal(1,m,t)+Ω(n,m,t)

(26)

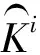
(27a)

当n为偶数时，

(27b)

其中,s(1,m,t)见式(20)。当n为偶数时

(28a)

当n为奇数时，

(28b)

当t→∞时，

(29)

当m→∞时，

(30)

当n→∞时，

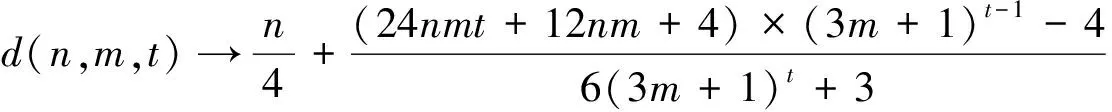
(31)

图5b所示为网络K(3,m,t)的平均最短路径长度d(3,m,t)，显然网络K(n,m,t)的平均路径长度d(n,m,t)性质与子网络K(1,m,t)一致，都是与t线性相关；当m较大时，与m基本上线性相关。可见，Koch网络性质主要决定于网络迭代生成的方式。

3.4网络直径

显然，Diam(1,m,0)=0，Diam(1,m,1)=2，且由网络K(1,m,t+1)的生成机制可知，Diam(1,m,t+1)=Diam(1,m,t)+2，所以

Diam(1,m,t)=2t～t

(32)

(33)

当正多边形边数n为有限值时，网络K(n,m,t+1)直径与网络大小对数成正比。

3.5度相关性

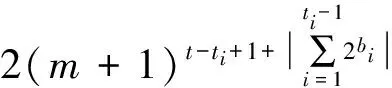
4m×(t-ti)×(m+1)t-ti-1)/2(m+1)t-ti

(34)

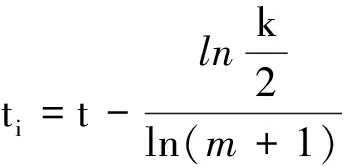
(35)

可得knn(1,k)～k-ω，即knn(1,k)随k的增大而减小，表示度值大的节点倾向于和度值小的节点连接，网络被看作是反向匹配的。

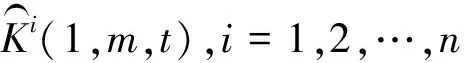
(36)

3.6节点的介数中心性

网络节点的重要性可以通过节点的中心性来衡量。定义节点v的介数中心性为

(37)

(38)

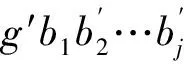
(39a)

(39b)

(40)

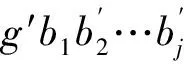
(41a)

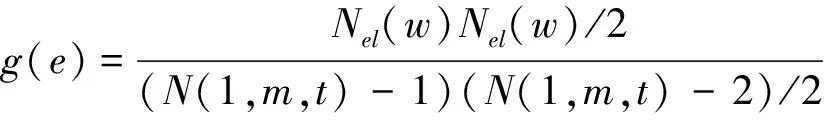
(41b)

4　结论

本文针对正多边形Koch分形岛映射成的复杂演化Koch网络，给出一种包含节点接入网络时间与精确位置信息的节点标号方法；并基于节点标号，研究了任意节点间的最短路由算法；并推导Koch网络的多种重要结构性质的解析解。结果表明：1)Koch网络的结构性质主要取决于分形的生成子，即Koch分形映射为复杂网络的映射方式，与分形的启动子基本无关。也就是说，Koch网络的结构性质主要决定于网络的迭代生成方式，与正多边形的边数基本无关。2)由Koch网络的主要结构性质的解析解可知，Koch网络是无标度网络，其幂指数为(2，3]；网络具有小世界特性，平均最短路径长度与网络大小的对数成比例；网络具有很高的聚类系数，聚类系数随着迭代结构参数m和迭代步数t的增加而趋于常数；网络直径与网络大小的对数成比例；度相关函数随节点度的增大而减小，表示度值大的节点倾向于和度值小的节点连接，网络被看作是反向匹配的；节点的点介数和边介数中心性都与节点度成指数关系。3)Koch网络可以采用一种基于节点接入网络时间和位置信息的方法进行标号，从而可以方便研究网络的最短路由、最短路径长度和介数中心性等网络性质的解析解，这也是本文的主要创新点。4)论文[17]中Koch网络为本文中n=3时的特例。

平面Koch网络是一种节点数目和边数目都是指数增加的演化网络，网络直径与网络规模的对数成正比，同时具备无标度、小世界和高聚类系数等特性，并且是负指数度相关的异配网络，这些性质与不少实际网络如因特网等相同，这说明平面Koch网络是可以作为研究大型复杂网络定量性质的网络模型。另外，平面Koch网络存在诸多的变形和拓展，如正多边形Koch网络、正多面体Koch网络、有权正多边形Koch网络等，针对这些确定性模型还只是进行了比较初步的研究，尚未得到最短路由、最短路径长度和介数中心性等网络性质和一些动力学过程的解析解，值得使用本文研究的节点标号法进行更进一步的相关研究。鉴于复杂演化Koch网络结构性质与很多实际网络相同，可以利用此网络能够解析求解的优点，对节点数目巨大的复杂网络中很多重要的结论如随机游走、谱特性、相继故障、博弈、同步与控制、传播、网络参数辨识进行更加深入的定量研究和发现。

[1]Watts D J， Strogatz S H. Collective dynamics of ‘small-world’networks[J]. nature， 1998， 393(6684)： 440-442.

[2]Barabási A L， Albert R. Emergence of scaling in random networks[J]. science， 1999， 286(5439)： 509-512.

[3]章忠志， 周水庚， 方锦清. 复杂网络确定性模型研究的最新进展[J]. 复杂系统与复杂性科学， 2008， 5(4)：29-46.

Zhang Zhongzhi， Zhou Shuigeng， Fan Jinqing. Recent progress of deterministic models forcomplex networks[J]. Complex Systems and Complexity Science， 2008， 5(4):29-46.

[4]Comellas F， Ozon J， Peters J G. Deterministic small-world communication networks[J]. Information Processing Letters， 2000， 76(1)： 83-90.

[5]Zhang Z， Zhou S， Qi Y， et al. Topologies and Laplacian spectra of a deterministic uniform recursive tree[J]. The European Physical Journal B-Condensed Matter and Complex Systems， 2008， 63(4)： 507-513.

[6]Barabási A L， Ravasz E， Vicsek T. Deterministic scale-free networks[J]. Physica A： Statistical Mechanics and its Applications， 2001， 299(3)： 559-564.

[7]Zhou T， Wang B H， Hui P M， et al. Topological properties of integer networks[J]. Physica A： Statistical Mechanics and its Applications， 2006， 367： 613-618.

[8]李永，方锦清，刘强. 多种确定性广义Farey组织的网络金字塔[J].物理学报，2010，05：2991-3000.

Li Yong， Fan Jingqing， Liu Qiang. Determinate generalized Farey organized network pyramid[J]. Acta Physica Sinina， 2010，05：2991-3000.

[9]Andrade Jr J S, Herrmann H J, Andrade R F S, et al. Apollonian networks: simultaneously scale-free, small world, euclidean, space filling, and with matching graphs[J]. Physical Review Letters, 2005, 94(1): 018702.

[10] Zhang Z, Chen L, Zhou S, et al. Exact analytical solution of average path length for Apollonian networks[J]. arXiv preprint arXiv:0706.3491, 2007.[DB/OL].[2014-05-06]. http://arxiv.org/abs/0706.3491.

[11] 邢长明，刘方爱.基于Sierpinski分形垫的确定性复杂网络演化模型研究[J].物理学报，2010，59(3)：1608-1614.

Xing Chang-ming， Liu Fan-ai. [J]. Research on the determinstic complex network model based on the Sierpinski network[J]. ACTA PHYSICA SININA， 2010，59(3)：1608-1614.

[12] Zhang Z, Zhou S, Fang L, et al. Maximal planar scale-free Sierpinski networks with small-world effect and power law strength-degree correlation[J]. EPL (Europhysics Letters), 2007, 79(3): 38007.

[13] Zhang ZH ZH， Qi Y， Zhou SH G，et al. Explicit determination of mean first-passage time for random walks on deterministic uniform recursive trees[J]. Physical Review E， 2010， 81：016114.

[14] Zhang ZH ZH， Yang Y H， Gao SH Y. Role of fractal dimension in random walks on scale-free networks[J]. European Physical Journal B， 2011， 84：331-338.

[15] Wu B， Zhang ZH ZH， Chen G R. Properties and applications of Laplacian spectra for the Koch networks[J]. Journal of Physics A： Mathematical and Theoretical， 2012， 45：025102.

[16] Zhang ZH ZH， Shan T， Chen G R. Random walks on weighted networks[J]. Physical Review E， 2013， 87：012112.

[17] Zhang Z， Wu B， Comellas F. The number of spanning trees in Apollonian networks[J]. Discrete Applied Mathematics， 2014， 169： 206-213.

[18] Zhang Z， Gao S， Chen L， et al. Mapping Koch curves into scale-free small-world networks[J]. Journal of Physics A： Mathematical and Theoretical， 2010， 43(39)： 395101.

[19] Zhang Z， Zhou S， Xie W， et al. Standard random walks and trapping on the Koch network with scale-free behavior and small-world effect[J]. Physical Review E， 2009， 79(6)： 061113.

[20] Zhang Z, Gao S, Xie W. Impact of degree heterogeneity on the behavior of trapping in Koch networks[J]. Chaos: an Interdisciplinary Journal of Nonlinear Science, 2010, 20(4): 043112.

[21] Zhang Z, Gao S. Scaling of mean first-passage time as efficiency measure of nodes sending information on scale-free Koch networks[J]. The European Physical Journal B-Condensed Matter and Complex Systems, 2011, 80(2): 209-216.

[22] 刘甲雪，孔祥木.无标度立体Koch网络的建立及其结构性质研究[J].物理学报，2010，4：2244-2249.

Liu Jia-xue， Kong Xiang-mu. Establishment and structure properties on scale-free Koch network[J]. Acta Physica Sinna， 2010，4：2244-2249.

[23] Chen R, Fu X, Wu Q. On topological properties of the octahedral Koch network[J]. Physica A: Statistical Mechanics and its Applications, 2012, 391(3): 880-886.

[24] Zhang J, Sun W. The structural properties of the generalized Koch network[J]. Journal of Statistical Mechanics: Theory and Experiment, 2010, (7): P07011.

[25] Zhang J Y, Sun W G, Chen G R. Exact scaling for the mean first-passage time of random walks on a generalized Koch network with a trap[J]. Chinese Physics B, 2012, 21(3): 8901.

[26] Sun W, Zhang J, Wu Y. Novel evolving small-world scale-free Koch networks[J]. Journal of Statistical Mechanics: Theory and Experiment, 2011, 2011(3): P03021.

[27] Wu Z K, Hou B Y, Zhang H S, et al. Scaling of average weighted shortest path and average receiving time on weighted expanded Koch networks[J]. International Journal of Modern Physics B, 2014, 28(28):2699-2700.

[28] Zhang Z， Comellas F， Fertin G， et al. Vertex labeling and routing in expanded Apollonian networks[J]. Journal of Physics A： Mathematical and Theoretical， 2008， 41(3)： 035004.

[29] Comellas F， Miralles A. Vertex labeling and routing in self-similar outerplanar unclustered graphs modeling complex networks[J]. Journal of Physics A： Mathematical and Theoretical， 2009， 42(42)： 425001.

[30] Comellas F， Miralles A. Label-based routing for a family of scale-free， modular， planar and unclustered graphs[J]. Journal of Physics A： Mathematical and Theoretical， 2011， 44(20)： 205102.

(责任编辑李进)

The Structural Properties of Koch Networks Based on Node Labels

ZHAI Yinhua,b， WANG Yinhea

(a.School of Automation， b.School of Information Engineering， Guangdong University of Technology， Guangzhou 510006， China)

The Koch Fractal Island， which is starting from a regular polygon， is mapped to complex evolving Koch networks. The informative labels are given to nodes， the labels are based on the time and location when nodes are accessing to Koch networks. By the advantages of the informative labels， we get the exact solution of main structural properties of Koch networks， including degree distribution and cumulative degree distribution function， as well as the clustering coefficient， average shortest path length and the correlation function of degree， betweenness centrality and the shortest path routing and length. The results show that， Koch network is a scale-free and small-world network; its clustering coefficient tends to relatively large constant; average shortest path length is proportional to the logarithm of the size of networks; degree correlation function is exponential function relationship with node's degree.

Koch networks; node labeling; network property; shortest path routing

1672-3813(2016)03-0058-11;DOI:10.13306/j.1672-3813.2016.03.008

2015-01-15；

2015-05-21

国家自然科学基金(61273219;F030203)

翟因虎(1974-)，男，江西奉新人，博士研究生，讲师，主要研究方向为复杂网络辨识与控制等。

TP1；N94

A