基于惯性坐标系旋转调制的INS辅助跟踪环路误差分析∗

张昀申

1 引言

INS/GNSS组合导航系统充分发挥惯性导航系统（Inertial Navigation System ，INS）与全球导航卫星系统GNSS（Global Navigation Satellite System）的各自优势，采用INS辅助GNSS接收机信号捕获、跟踪的深组合模式，能提高导航系统精度，拓展导航系统的应用范围。同时，INS的器件的陀螺仪漂移、加速度计零偏以及标度因数误差会增加辅助跟踪环路误差，文献［1］对INS辅助信息误差引起的跟踪环路误差做了分析。文献［2］中美国海军采用旋转调制技术实现了对IMU系统所有误差进行有效补偿，文献［3］的旋转方法对标度因数误差和安装误差带来的载体角运动相关误差项的补偿作用有限。文献［4］的方法可以抵消标度因数误差。

本文采用基于惯性坐标系的旋转调制方法补偿INS器件的标度因数误差，从而有效减少标度因数误差对INS/GNSS组合导航系统跟踪环路误差的影响。

2 IMU标度因数类误差

IMU辅助载波跟踪环路误差包括IMU零偏类误差、标度因数类误差和多普勒辅助延迟。图1是辅助载波跟踪环的原理框图［1］。

在忽略热噪声和晶振影响的前提下，假设前馈支路只具有标度因数类误差Ka(s)，IMU标度因数类误差的传递模型如图2所示［5］。

IMU标度因数类误差引起的跟踪误差δθ(s) 为［6］

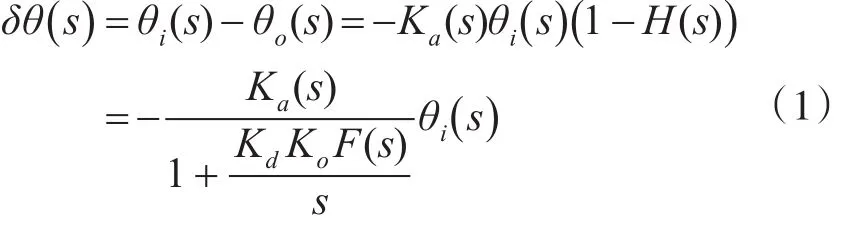
图1 INS辅助载波跟踪环路原理框图

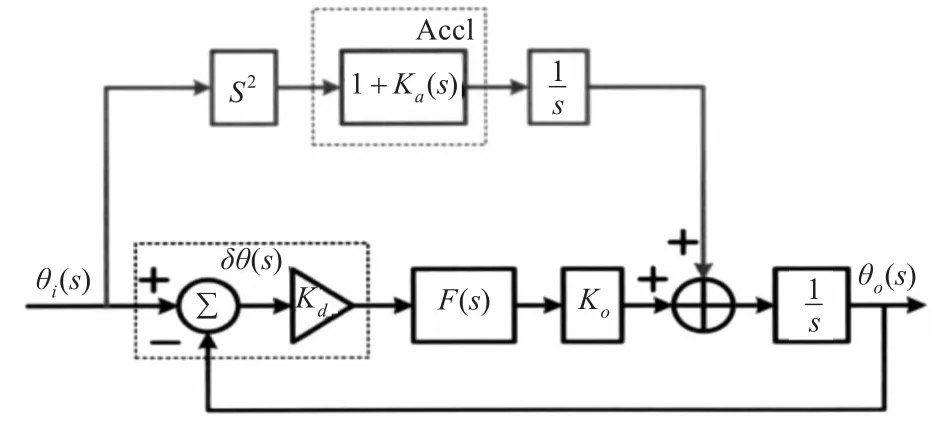
图2 IMU标度因数类误差的传递模型

θi(s)是输入信号，θo(s)是输出信号，Kd是鉴别器增益，Ko是数控振荡器控制增益，在标度因数类误差的传递模型中引入二阶跟踪环的滤波器传递函数，得到由IMU标度因数类误差产生的二阶跟踪环误差模型是

ξ为阻尼系数，ωn是自然角频率。因为频率斜升信号对二阶环路影响比较大，所以在对IMU标度因数类误差进行分析时，将频率斜升的输入信号作为主要对象进行计算，即θi(s)=Δℜ/s3，将激励信号带入式（2），则有［7］

将式（3）进行拉普拉斯反变换，得出环路误差与IMU标度因数类误差的时域模型。为简化模型，ξ=1。

已有文献［1］研究发现标度因数误差越小，其引起的辅助跟踪环路误差越小，其中的标度因数误差Ka为随机常数。接下来，本文将利用基于惯性坐标系旋转调制来减少标度因数误差，从而减少由其引起的辅助跟踪环路误差。

3 基于惯性坐标系旋转调制

组合导航系统中旋转调制型IMU的误差模型可以用下式表示［8，9］：

式中：Cns表示从s坐标系到n坐标系的转换矩阵，f、δf表示比力和加速度计测量误差，n表示导航坐标系，e表示地球坐标系，b表示载体坐标系，s表示IMU坐标系，i表示地心惯性系，Φ为失准角；ω、δω分别表示角速度和陀螺仪测量角速度误差；δg表示重力偏差；V、δV分别表示速度和速度误差。

组合导航系统中，陀螺仪和加速度计的输出误差模型为［12］

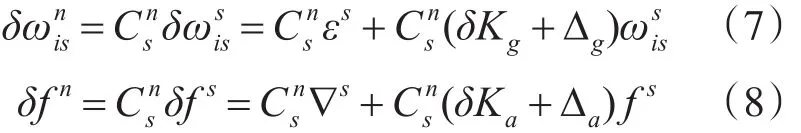
式中：ωsis为陀螺敏感轴输入角速度，Δg为陀螺仪的安装误差、δKg为标度因数误差、εs为常值漂移；fs为加速度计敏感轴输入信息，Δa为加速度计安装误差，δKa为标度因数误差、∇s为零偏。

对于δfn在一个旋转周期内进行积分，得到：

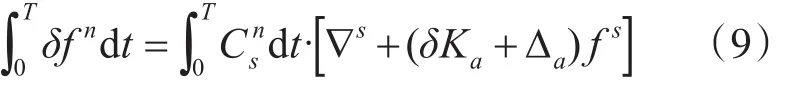
式中定义逆时针旋转为正，T为一个旋转调制周期，Cns为常值矩阵。加速度计累计输出误差由两部分组成，第一项为常值漂移误差，第二项是旋转机构转速与δKa和Δa的耦合误差，当载体运动加速度变化时，加速度变化信息与误差一起通过加速度计输出，在一个旋转周期内，采用多次旋转可以使式（9）中两项误差Cns的累加积分值为零，因此加速度计输出误差能通过旋转消除。

加速度计标度因数误差对辅助跟踪环路误差的累计影响可以用下式描述：

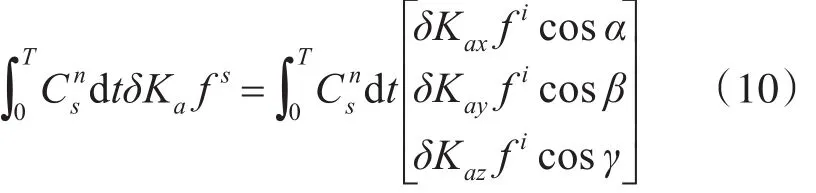
式中δKai（i=x，y，z）表示三轴加速度计标度因数误差。

为抵消标度因数误差影响，要保证δKaxficosα ，δKayficosβ ，δKazficosγ在两个旋转过程中完全相同，只有两个旋转方向相反的旋转过程成对出现时，才能满足 ficos X（X=α，β，γ）的每两组结果互为相反数，从而减少标度因数误差对辅助跟踪环路误差的影响。

（7）（8）两式形式类似，能够抵消加速度计标度因数误差的旋转方案也能抵消陀螺的标度因数误差。

4 仿真验证

选用同一中等精度惯导，其标度因数典型值为300ppm，环路带宽10Hz，地理坐标系和载体坐标系重合，所在位置为32.03°N，118.46°E。

设计旋转方式按照IMU初始时刻绕惯性坐标系Z轴正向旋转的过程，必须与其绕Y轴旋转180°后，再绕Z轴反向旋转的过程成对出现，同理可知，绕其他轴的正反向旋转过程也需成对出现，才能达到满足 ficos X（X=α，β，γ）的每两组结果互为相反数的要求，从而减少标度因数误差对辅助跟踪环路误差的影响。

在二十四小时内采样，分别绘制无惯性坐标系旋转调制和有惯性坐标系旋转调制两种情况的辅助跟踪环路误差曲线，如下图所示。

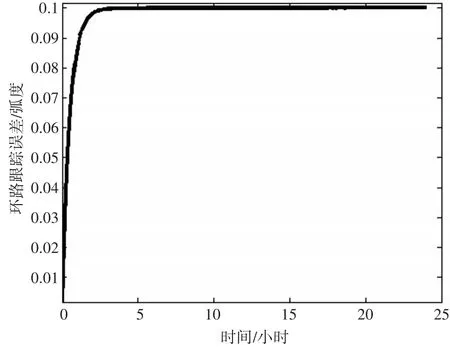
图3 无惯性坐标系旋转调制跟踪环路误差

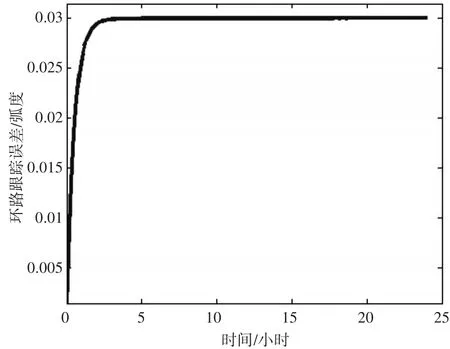
图4 惯性坐标系旋转调制后跟踪环路误差

在仿真初始阶段，辅助跟踪环路误差随时间向上增长，之后误差随时间推移逐渐趋于稳定，由于采用了基于惯性坐标系的旋转调制方法，抵消了加速度计的标度因数误差，有效抑制了标度因数误差引起的辅助跟踪环路误差。

5 结语

本文通过对IMU辅助跟踪环路误差中标度因数类误差进行分析，采用基于惯性坐标系旋转调制方法，将标度因数误差抵消，从而降低了由标度因数误差引起的辅助跟踪环路误差的影响。为进一步改善整个INS/GNSS组合导航系统的性能提供了参考，为深入研究深组合技术提供了支撑，是在不更换现有元件的情况下提高系统精度的一种有效方法。

［1］张提升.GNSS/INS标量深组合跟踪技术研究与原型系统验证［D］.武汉：武汉大学，2013（9）：10-11.

［2］Dr.E.Levinson，J.Ter Horst，M.Willcocks.The Next Generation Marine Inertial Navigator is Here Now［C］//Proc.of the IEEE Position Location and Navigation Sympo⁃sium，1994：121-127.

［3］马晓峰.基于旋转调制技术的微小型水下机器人导航技术研究［D］.上海：上海交通大学，2011（12）：31-32.

［4］孙枫，王秋滢.三轴旋转捷联惯导系统旋转方案设计［J］.仪器仪表学报2013，34（1）：65-72.

Yang，Y.Tightly coupled MEMSINS/GPSintergation with INS aided receiver tracking loops［D］.Calgary：University of Calgary，2008：67-68.

Sun D.Ultra-Tightly GPS/Reduced IMUfor Land Vehicle Navi⁃gation［D］.Calgary：University of Calgary，2010：56-58.

［7］R.Vaccaro，A.Zaki.Statistical Modeling of Rate Gyros［J］.IEEE Transactions on Instrumentation and Measure⁃ment.2012（61）：673-684.

［8］TITTERTON D H，WESTON J L． Strapdown inertial na⁃vi-gation technology［M］.2nd ed． Lexington，Massaehu⁃setts：MITLincoln Laboratory，2004：14-29.

［9］袁保伦，饶谷音.光学陀螺旋转惯导系统原理探讨［J］.国防科技大学学报，2006，28（6）：76-80.

［10］Cong L，Qin H L，Tan Z Z.Intelligent fault-toler⁃ant algorithm with two-stage and feedback for inte⁃grated navigation federated filtering［J］.Systems Engi⁃neering and Electronics.2011，22（2）：274-282.

［11］Moussa，A.，A.S.Ali，N.El-Sheimy.The Effect of Time Synchronization on Real Time Implementation of Integrat⁃ed GPS/INSSystems［C］//Proc.of ION ITM，San Diego，CA.2010：43-48.

［12］孙伟.调制型捷联惯性导航系统技术研究［D］.哈尔滨：哈尔滨工程大学，2011：57-60.