基于分布式估计与模糊控制的多机器鱼编队控制

李宗刚,郭志龙,石慧荣,谢广明

(1.兰州交通大学机电工程学院,兰州 730070；2.北京大学工学院系统与控制研究中心,北京 100871)



基于分布式估计与模糊控制的多机器鱼编队控制

李宗刚1,2,郭志龙1,石慧荣1,谢广明2

(1.兰州交通大学机电工程学院,兰州 730070；2.北京大学工学院系统与控制研究中心,北京 100871)

针对多仿生机器鱼编队控制问题，提出了一种分布式的分层控制方案。首先，各机器鱼以一致性算法为数据融合模块对编队中心位姿进行分布式估计，据此获得在编队中的期望位姿，作为路径规划模块的输入；其次，各机器鱼基于速度与方向模糊控制器，实时跟踪期望轨迹，形成和保持编队。所提方法实现了期望位置分布式估计与机器鱼个体路径规划的分离，为不同种类机器鱼的合作控制问题提供了新思路。实验结果表明了所提方法的有效性。

仿生机器鱼;编队;一致性算法;模糊控制;轨迹跟踪

0　引言

近年来，随着海洋重要性的日益凸显，海洋中的地图构建、生态监测、水中侦测等领域的需求使得多水下机器人系统的协调控制问题成为多机器人系统研究的热点[1-9]。针对水环境的动态特性所造成位姿的不确定性，Zhang等[3]利用提出的极限环方法控制机器鱼位姿和避免碰撞，利用模糊控制器控制方向，研究了多鱼协作搬运任务。文献[4]研究了多机器鱼协作爆破问题，其中利用遗传算法优化机器鱼之间的权重因子，进而利用改进的匈牙利算法实现了任务分配。Shao等[5]利用机器鱼的机构特点，利用曲率坐标系建立了个体动力学模型，进而基于领航者-跟随者方法研究了多机器鱼编队控制问题。Zou等[6]利用基于径向基神经网络的滑模控制方法研究了多机器鱼的轨迹跟踪问题。Zhao等[7]基于领航者-跟随者方法研究了多自主机器鱼的编队的控制问题。其中，机器鱼线速度和角速度分别通过模糊控制器和期望Bezier轨线曲率优化方法进行控制。Hu等[10]提出了一种基于劳动分工方法的多自主机器鱼搬运控制策略。此外，文献[8]～[9]基于行为技术研究了多水下机器人编队控制问题。需要指出的是，文献[3]～[9]中的协调控制算法都是集中式的，也即机器鱼之间不存在信息交互,文献[10]的算法是分布式的，其特点更近于通过公平竞争的方式完成协作任务。

针对空中或地面多机器人系统，基于领航者-跟随者方法和一致性算法的编队控制策略得到了广泛研究[11-22]。受此启发，本文以三关节仿鲹科机器鱼为对象，提出了一种分层的多仿生机器鱼分布式编队控制算法。其中，以期望队形的几何中心作为虚拟领导者，首先每个机器鱼利用一致性算法对编队中心位姿进行分布式估计，进而基于估计信息和编队要求确定自身下一时刻的位姿，最后利用模糊控制器控制机器鱼的线速度和角速度，实现对期望位姿的精确跟踪。所提方法将一致性算法作为数据融合模块，利用领航者-跟随者模式实现编队控制。

1　预备知识

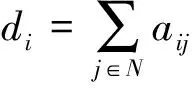
对所考虑的多机器鱼系统，令pi(t)=[xi(t),yi(t),θi(t)]T∈R3表示机器鱼vi的位姿信息，则必有

(1)

其中，θi表示机器鱼头尾轴与x轴的夹角，υi∈[0,υmax]表示机器鱼巡游速度，ωi∈[0,ωmax]表示机器鱼转弯角速度。机器鱼之间的信息交换拓扑满足假设1。

假设1设有向图G为N条机器鱼组成的多智能体系统的信息交换拓扑，则G含有生成树，且在任意时刻至少有一个根节点可以接收到参考轨迹的位姿信息ξ0(t)。

2　多仿生机器鱼编队控制

考虑N个多仿鲹科三关节机器鱼的编队控制问题，机器鱼的体波曲线由Lighthill方程

ybody(x,t)=(c1x+c2x2)sin(kx+ωt)

(2)

控制。则所考虑多仿生机器鱼编队控制问题可描述为：在沿期望轨迹运动的过程中，N条机器鱼头部参考点的连线形成并保持期望的队形，同时所有机器鱼头尾轴的方向最终保持一致。分析可知，各机器鱼在编队形成与保持的过程中，通过直线巡游中的转弯行为调整位姿，其巡游速度和转弯角速度由式(1)和式(3)给出。为此，提出一种基于个体的编队形成与保持方法，机器鱼vi的位姿控制流程如图1所示。

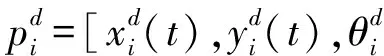
2.1编队参考点一致性估计

在编队形成与保持过程中，多采用个体之间的位姿偏置量确定编队形状[15-16，18-20]。受此启发，本文以编队几何中心为参考点，确定各机器鱼在编队中的相对位姿，如图2所示。

由于所考虑的多机器鱼系统信息交换拓扑满足假设1，为了实现编队，各机器鱼必须基于局部信息实现编队任务。由于机器鱼vi在编队中的位姿是确定的，因此可以根据其当前位姿估计出编队参考点位姿ζi(t)，并同相邻机器鱼共享这一信息。基于这一事实，利用一致性算法对编队参考点进行分布式估计，协议为

(3)

i=1,…,N，ζi(t),ζj(t)分别表示第i条和第j条机器鱼所估计的参考点位姿；ξ0(t)表示编队所要跟踪的轨迹，当机器鱼i能够获得所跟踪轨迹的位姿信息时，bi0=1，否则为0。易知，式(4)是典型的一阶一致性算法，由文献[19]中的定理3.1可知，式(4)描述的多机器鱼编队参考点位姿估计算法，当信息交换拓扑满足假设1时，当t→∞时，必有ζi(t)→ζ0(t)成立。

需要指出的是，一致性算法(4)仅作为数据融合模块存在，通过分布式方法为各机器鱼的轨迹规划提供支持。由于水中环境的动态特性带来的不确定性，使得很难对机器鱼进行精确控制，多机器鱼组成的编队也很难保持。这一点也是实现水中多仿生机器鱼编队控制的难点。

2.2多机器鱼编队形成与保持

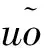
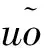
(4)

在编队保持和轨迹跟踪阶段，机器鱼以巡游转弯行为保持其在编队中的位姿，此时体波方程(3)在由式(1)确定的υi和ωi确定后起作用。为了实现编队保持和跟踪期望轨迹的目标，需要设计精确控制机器鱼由式(1)确定的直线巡游速度υi和转弯角速度ωi的控制律。

3　多机器鱼编队路径跟踪模糊控制器

如何克服水环境的动态特性对多机器鱼编队形成、保持与轨迹跟踪带来的不确定性，是实现上述任务的关键。受文献[3],[21]～[24]的启发，采用模糊控制方法对机器鱼的运动方向和速度进行控制。

由图4可知，机器鱼vi与其期望位置之间的距离为

(5)

易得期望位姿的方向角为

则机器鱼vi与其期望位姿之间的方向角之差为

(6)

控制目标即是使得由式(6)及式(7)确定的误差信号为零。机器鱼vi的角速度ωi及速度υi的模糊控制器结构如图5所示。

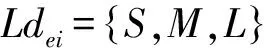
与此相对应，输出υi由3条模糊控制规则获得，即IfdeiisS, thenυiisS;IfdeiisM, thenυiisM;IfdeiisL, thenυiisF。

每条模糊规则的激活度ηi由Mamdani推理规则确定，即ηi=min(μ(dei)),i=1,2,3,μ(dei)为模糊变量Ldei值的隶属度函数值，则机器鱼vi的巡游速度可由“重心法”去模糊得到，即

(7)

下面讨论机器鱼vi的方向控制问题，其方向模糊控制器输入为角度误差θei，由于-π≤θei(t)<π，故将其分为7个等级，对应模糊集记为

分别表示负大、负中、负小、零、正小、正中、正大，其隶属度函数如图7a所示。同理，方向模糊控制器的输出变量为角速度ωi，其模糊集记为

分别表示负大、负中、负小、零、正小、正中、正大，隶属度函数如图6b所示。

与此相对应，输出ωi由以下模糊规则得到：IfθeiisPB,thenωiisPB;IfθeiisPM,thenωiisPM;IfθeiisPS,thenωiisPS;IfθeiisZE,thenωiisZE;IfθeiisNS,thenωiisNS;IfθeiisNM,thenωiisNM;IfθeiisNB,thenωiisNB。

每条模糊规则的激活度μi由Mamdani推理规则确定，即μi=min(μ(θei)),i=1,…,7,μ(θei)为模糊变量Lθei值的隶属度函数值，则机器鱼vi的角速度可由“重心法”去模糊得到，即

(8)

机器鱼vi通过模糊控制器获得其下一时刻的巡游速度υi和角速度ωi之后，即依据式(3)选择合适模态进行游动，以达到保持编队和跟踪期望轨迹的目标。

4　实验

4.1单仿生机器鱼路径跟踪

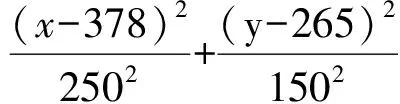
如图9所示，机器鱼以逆时针方向游动，其轨迹基本能够跟踪参考椭圆轨迹。图10，图11以及图12分别是机器鱼跟踪椭圆轨迹时的线速度，运动方向和角速度的变化曲线。

由上述各图可知，机器鱼编队的线速度基本维持在10～16cm/s的恒定范围内。12s时，由于运动滞后的原因发生跳变，但角度及角速度保持稳定；在24s时，游动到图8所示的b点，运用游动中的转弯方式进行转弯，其线速度增大，以增加回摆的力度，为跟踪椭圆轨迹，运动方向瞬间由3rad转为-3rad，此时，由于速度和运动方向的改变，其转弯角速度也瞬间降为-7rad/s,为最小。之后，在恒定速度下，运动方向趋于0，在50s时，游动到图8所示的d点，发生另一次游动中转弯。之后游动到a点，完成一个周期的编队巡游。由图可见，机器鱼的速度和角速度变化都符合模糊控制规则的设计要求，表明在模糊控制器的作用下，机器鱼能够稳定地跟踪期望的参考轨迹。

4.2多机器鱼编队形成与保持

考虑3条仿生机器鱼的三角编队及轨迹跟踪问题，实验环境为的室内水池，机器鱼初始位置在水池左侧随机布置，编队中心参考轨迹为直线。3条仿生机器鱼在水池中的运动场景如图13所示。由图可知，3条仿生鱼在8s时已形成期望队形，并在后续过程中保持了队形。图14为3条机器鱼的运动轨迹图，可以看出，编队在跟踪一直线时表现比较稳定。图15给出了各机器鱼在游动中的线速度变化情况，其中红线代表编队中心的期望速度。由图可知，为了保持编队，机器鱼的游动速度始终有微小的波动。

图16、图17和图18分别给出了机器鱼的方向、角速度以及实际的误差曲线。由图可知，各机器鱼线速度，角速度的变化基本趋于一致，表明3条机器鱼能够快速地形成编队，并且在保持编队构型的前提下，实现了对参考轨迹曲线的精确跟踪。

5　结论

针对多仿生机器鱼的编队控制问题，基于分层思想，提出了一种分布式的控制算法。在该方案中，首先每条机器鱼采用一致性算法模块对编队中心信息进行分布式估计，并据此求得其下一时刻在编队中的期望位姿；其次，各机器鱼采用模糊控制器确定自己的巡游速度和转弯速度，从而实现对期望位姿的跟踪，实验结果表明算法是有效的。所提方法兼顾了编队算法的分布性和机器鱼本身的动力学特性，实现了一致性算法与机器人动力学的分离，为不同种类机器人之间的合作控制问题提供了一个新的思路。在后续工作中，将综合考虑编队参考点信息的变化率及其不确定性，以及模糊控制器输入变量的变化率信息，设计更灵敏和可靠的合作控制算法，提高多仿生机器鱼协作编队任务的稳定性和准确性。

[1]Zhang Y, Streitlien K, Bellingham J G, et al. Acoustic doppler velocimeter flow measurement from an autonomous underwater vehicle with applications to deep ocean convection[J]. Journal of Atmospheric and Oceanic Technology, 2001, 18(12): 2038-2051.

[2] Leonard N E, Fiorelli E. Virtual leaders, artificial potentials and coordinated control of groups[C]// Proceedings of the 40th IEEE Conference on Decision and Control. Orlando,Florida,USA,2001, 3: 2968-2973.

[3] Zhang D D, Wang L, Yu J Z, et al. Coordinated transport by multiple biomimetic robotic fish in underwater environment[J]. IEEE Transactions on Control Systems Technology, 2007, 15(4): 658-671.

[4] Zhang D D, Wang L, Yu J Z. Geometric topology based cooperation for multiple robots in adversarial environments [J]. Control Engineering Practice, 2008, 16(9): 1092-1100.

[5] Shao J Y, Yu J Z, Wang L. Formation control of multiple biomimetic robotic fish[C]// Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. Beijing, China, 2006: 2503-2508.

[6] Zou K M, Wang C, Xie G M, et al. Cooperative control for trajectory tracking of robotic fish[C]. 2009 American Control Conference. St Louis, MO, USA, 2009: 5504-5509.

[7] Zhao W, Hu Y H, Wang L. Leader-following formation control of multiple vision-based autonomous robotic fish[C]∥Proceedings of the 48th IEEE Conference on Decision and Control, 2009 held jointly with the 2009 28th Chinese Control Conference. Shanghai, China, 2009, 579-584.

[8] 孟宪松, 徐宏根, 张铭钧, 等. 基于分解策略的多机器人编队控制方法[J]. 哈尔滨工程大学学报，2006, 27(2): 276-280.

Meng Xiansong, Xu Honggen, Zhang Mingjun, et al. Formation control for multiple robots based on a strategy of decomposition [J]. Journal of Harbin Engineering University, 2006, 27(2): 276-280.

[9] 范士波, 王宏健. 多自主水下航行器编队控制技术研究[J]. 中国造船，2008, 50(4): 92-101.

Fan Shibo, Wang Hongjian. Research on formation technology for autonomous underwater vehicles[J]. Ship Building of China, 2008, 50(4): 92-101.

[10] Hu Y H, Wang L, Liang J H, et al. Cooperative box-pushing with multiple autonomous robotic fish in underwater environment [J]. IET Control Theory and Applications, 2011,5(11): 2015-2022.

[11] Shao J Y, Xie G M, Yu J Z, et al. Leader-following formation control of multiple mobile robots[C]∥Proceedings of the 2005 IEEE Internatio-nal Symposium on Mediterrean Conference on Control and Automation, IEEE.Limassol, Cyprus, 2005: 808-813.

[12] Chen Y, Zhuang Y, Wang W. Cooperative control for formations of mobile robots under the nonholonomic constraints[C]∥Proceeding of the 6th World Congress on Intelligent Control and Automation, IEEE.Dalian, China， 2006, 2: 9042-9046.

[13] Fax J A, Murray R M. Information flow and cooperative control of vehicle formations[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1465-1476.

[14] Lin Z Y, Francis B, Maggiore M. Necessary and sufficient graphical conditions for formation control of unicycles[J]. IEEE Transactions on Automatic Control, 2005, 50(1): 121-127.

[15] Porfiri M, Roberson D G, Stilwell D J. Tracking and formation control of multiple autonomous agents: a two-level consensus approach[J]. Automatica, 2007, 43(8): 1318-1328.

[16] 张博, 罗建军, 袁建平. 一种基于信息一致性的卫星编队协同控制策略[J]. 航空学报, 2010, 31(5): 1004-1013.

Zhang Bo, Luo Jianjun, Yuan Jianping. A satellite formation cooperative control strategy based on information consensus[J]. Acta Aeronautica et Astronaut Ica Sinica, 2010, 31(5): 1004-1013.

[17] Sheng L, Pan Y J, Gong X. Consensus formation control for a class of networked multiple mobile robot systems[J]. Journal of Control Science and Engineering-Special Issue on Advances in Methods for Control over Networks, 2012: 1-12.

[18] Cao Y C, Ren W, Sorensen N, et al. Experiments in consensus-based distributed cooperative control of multiple mobile robots[C]∥Proceedings of the 2007 IEEE International Conference on Mechatronics and Automation. Harbin, China， 2007: 2819-2824.

[19] Ren W, Sorensen N. Distributed coordination architecture for multi-robot formation control[J]. Robotics and Autonomous Systems, 2008, 56: 324-333.

[20] Fang L, Antsaklis P J A. Decentralized formation tracking of multi-vehicle systems with consensus-based controllers[J]. Advances in Unmanned Aerial Vehicles, Intelligent Systems, Control and Automation: Science and Engineering, 2007, 33: 455-471.

[21] Bazoula A, Djouadi M S, Maaref H. Formation control of multi-robots via fuzzy logic technique[J]. International Journal of Computers, Communications & Control, 2008, 3(3): 179-184.

[22] Amoozgar M H, Alipour K, Sadati S H. A fuzzy logic-based formation controller for wheeled mobile robots[J]. Industrial Robot: an International Journal, 2011, 38(3): 269-281.

[23] Liao Y, Huang J, Zeng Q. Preview fuzzy control method for intelligent vehicle path tracking[C] ∥Proceeding of 2010 IEEE International Conference on Progress in Informatics and Computing (PIC), IEEE, 2010, 2: 1211-1214.

[24] Antonelli G, Chiaverini S, Fusco G. A fuzzy-logic-based approach for mobile robot path tracking[J]. IEEE Transactions on, Fuzzy Systems, 2007, 15(2): 211-221.

(责任编辑李进)

Formation Control of Multiple Robotic Fish Based on Distributed Estimation and Fuzzy Control

LI Zonggang1,2， GUO Zhilong1， SHI Huirong1, XIE Guangming2

(1.School of Mechanic and Electronic Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China;2.Center for Systems and Control, College of Engineering, Peking University, Beijing 100871, China)

This paper proposed a distributed and hierarchical scheme for formation control of multiple robotic fish. Firstly, each robotic fish takes consensus algorithm as a distributed data fusion modular to estimate the center of the formation, and then calculate its desired position in the formation at the next time. Such estimated results are the input variables of its path planning modular. Secondly, each robotic fish tracking its desired position by employing the fuzzy controller of linear speed and angular speed in order to form and maintain formation. The proposed method separates the distributed estimation and the path planning and behavior of robotic fish, such a property gives a new method for the cooperative control of multiple heterogeneous robotic fish. The results of experiment shows the validity of the proposed method.

biomimetic robotic fish; formation control; consensus; fuzzy control; trajectory tracking

1672-3813(2016)03-0040-07;DOI:10.13306/j.1672-3813.2016.03.006

2015-06-05；

2015-12-31

国家自然科学基金(61064008);教育部科学技术研究重点项目(211185);甘肃省自然科学基金(1112RJZA042，1208RJZA166)

李宗刚(1975-)，男，宁夏西吉人，博士，副教授，主要研究方向为复杂系统动力学分析与控制、智能仿生机器人动力学及控制、智能信息处理。

TP273

A