基于非负矩阵分解的复杂网络重构

陈增强，谢　征，张　青

(1.南开大学计算机与控制工程学院天津市智能机器人技术重点实验室，天津 300071；2.中国民航大学理学院，天津 300300 )



基于非负矩阵分解的复杂网络重构

陈增强1,2，谢征1，张青2

(1.南开大学计算机与控制工程学院天津市智能机器人技术重点实验室，天津 300071；2.中国民航大学理学院，天津 300300 )

将网络连边的产生机制和其社团结构结合在一起，基于社团结构决定网络连边的假设推导出节点间的连接概率矩阵并表达为矩阵乘积的形式，然后利用非负矩阵分解得到节点间的连接概率矩阵进行网络重建。设计实验并在几个真实的网络数据上测试，相比基于相似度的网络重构算法，该算法取得了更好的网络重构效果。

复杂网络；网络重构；社团结构；连接概率矩阵；非负矩阵分解

0　引言

复杂网络[1-2]是研究自然界各种复杂系统的有力工具。通过对复杂系统进行观测和抽象，提取出一个由节点和连边构成的网络结构，进一步可以进行拓扑特性[3]、传播行为[4-5]和网络控制[6]等方面的分析研究。由于客观因素的限制，观测提取到的数据不能真实完整地反映实际网络包含的信息，比如存在未被观测到或者被错误观测的数据，这就影响到了后续对数据的分析操作。网络重构是解决此类问题的有效方法。网络重构[7]是指根据观测到的网络节点属性和结构信息，推断网络的真实结构，包括链路预测和虚假边识别两个部分。链路预测是预测节点之间可能会产生的连边或观测网络中不存在而真实网络中存在的连边，虚假边识别是识别观测网络中存在而真实网络中不存在的连边。网络重构最早由Guimerà等[8]提出，他们采用随机分块模型，认为网络是由群组组成，而节点之间连接的可能性取决于它所在的群组，基于极大似然分析得到各条连边的可信度来进行网络重构。Shen等[9]利用复杂网络的稀疏性，采用压缩感知理论来重构网络。现有的研究多集中在链路预测[10]上。Kleinberg等[11]认为节点之间的相似性越大，其间存在连接的可能性越大，提出许多基于节点和基于路径的相似性指标来进行链路预测。Zhou等[12]改进并设计了更高效的相似度指标。Clauset等[13]结合网络的层次结构，提出基于极大似然估计的链路预测模型。Gao等[14]综合考虑网络的多方面信息，提出一种结合网络拓扑、节点属性和局部相似性的链路预测方法。相比较，虚假边识别的研究较少。在链路预测过程中计算的节点相似性也可以用来做虚假边识别的指标[3]。

由于网络一般由邻接矩阵表示，网络的连边进行增删和权值改变即对应于邻接矩阵的相应元素进行改变，因此网络重构可看作是一个矩阵重建[15-16]问题。另一方面，网络的连接和其社团结构[17]也紧密相关。每个节点在网络中都有自己所扮演的“角色”，节点之间根据角色的相互作用产生连边。而节点的角色特征体现在它所属的社团中，社团结构的重叠性质又保证了节点可以扮演不同的角色，因此可以和更多的节点产生连边，保证了网络的多样性。基于上述分析，本文将网络的连边产生机制和其社团结构结合在一起，认为网络是由许多社团组成且节点之间连接的可能性取决于它所在的社团，基于此推导出节点间的连接概率矩阵，然后利用非负矩阵分解求解，并以得到的连接概率矩阵来推断真实的网络结构。在4个真实数据集上进行测试比较，发现该算法比基于节点相似性的算法能得到更好的重构效果。最后讨论了参数选取，正则化等因素对算法效果的影响。

1　基于非负矩阵分解的网络重构

1.1网络重构

和随机分块模型类似，本文做出两个基本假设。1)网络由许多社团[17]组成，任意节点都属于其中的至少一个社团。社团是网络中一种很普遍的结构，表示节点基于某种特征形成的一种集合，例如社交网络中的朋友圈，万维网中的主题分类，引文网络中的研究领域等等。不同于随机分块模型中的群组可以是节点的任意组合，社团结构要求社团内部联系紧密，社团之间连接稀疏。每一个节点都会在网络中扮演一定的角色，且由于节点角色的多样性，其所属社团可能会有多个。对于网络中出现孤立节点的特殊情况，也可以将孤立节点看作一个社团。2)节点之间连接的可能性取决于其所在的社团，即节点之间是通过其所在的社团之间的联系来产生连边。这是由于节点所在的社团一定程度上描述了节点的身份属性，而节点之间之所以产生连边是因为其各自身份属性的相互作用，故节点在社团中的成员身份决定其连接行为。由以上分析得出网络重构的基本思路：通过节点间的网络拓扑联系，推断节点的所属社团和其内在的身份属性，再由假设2)提出的网络生成演化机制来重新生成网络。

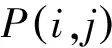
(1)

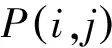
W=HSHT

(2)

矩阵W可以看作对原始邻接矩阵A的近似表达，即

A≈W=HSHT

(3)

至此，我们将原始的网络重构问题转化为一个非负矩阵分解问题，即寻找合适的非负矩阵H和S，使其满足式(3)的近似关系。

1.2非负矩阵分解

非负矩阵分解(Nonnegative Matrix Factorization，NMF)是将给定的非负矩阵近似分解为几个非负矩阵的乘积的形式。1999年Lee等[18]在Nature上发表了NMF算法，之后各种改进的NMF算法被提出以提升其性能和扩展其应用范围[19-20]。对于给定的非负矩阵V∈Rm×n，将其近似表达为两个非负矩阵W∈Rm×k和H∈Rk×n的乘积，即

V≈WH

(4)

一种简单的衡量这种近似程度的指标是误差矩阵的Frobenius范数：

(5)

为求解上述问题，文献[21]给出了一种乘性迭代规则

(6)

(7)

以同时满足目标函数的非增性和矩阵元素的非负性。

对于本文的网络重构问题，同样采用上述指标来衡量重构网络对原始观测网络的逼近程度，即

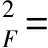
(8)

如果两个节点直接相连接代表代表其几何空间的邻近性，则其社团隶属度特征也应具有相应的邻近性。为了保持这种数据空间的几何特征，对原目标函数引入图正则化[22]，得到新的目标函数：

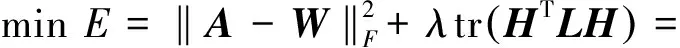
(9)

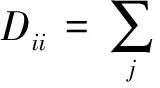
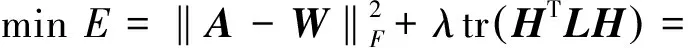
s.t. H>0,S>0,S=ST

(10)

借鉴文献[14]，本文给出了一种快速有效的迭代方法求解上述规划问题：

(11)

(12)

将上述算法归纳如下：

1) 确定网络邻接矩阵A，矩阵S的维度k，正参数λ以及指定误差限ε。

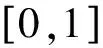
3)重复计算：通过式(11)和(12)计算H和S；通过式(9)计算优化目标值E；直到达到指定迭代次数或迭代满足误差限。

4)得到重构矩阵W及逼近误差(λ=0时的E值),节点的社团隶属度矩阵H和社团关系矩阵S。

本文中，将由目标式(8)计算重构矩阵的方法称为基于社团划分的非负矩阵分解(CNMF)，将由目标式(9)计算重构矩阵的方法称为基于社团划分的正则化非负矩阵分解(RCNMF)

2　实验及分析

2.1实验设计

为了检验该网络重构算法的有效性，将验证工作分为两部分：链路预测的准确性和虚假边识别的准确性。1)对于链路预测来说，首先将原始网络数据中已知的连边集E分为训练集E1和测试集E2两部分：E=E1∪E2，E1∩E2=Φ，把不属于原始数据集E的连边集合称为不存在的边集EN，并将其视为基准集EB；2)对于虚假边识别来说，首先随机生成一些原本不存在的边ESN⊂EN，将原始数据集E与随机生成的边合并为训练集E1=E∪ESN，将原始数据集E视为测试集E2=E，并将随机生成的边集视为基准集EB=ESN。对于这两种情况，在迭代计算重构网络的过程中只使用训练集E1的数据，得到重构网络W为节点之间连接的概率。

本文采用AUC指标衡量算法的精确度，即每次随机地从测试集E2选取一条边linkE2并随机地从基准集EB选择一条边linkEB，比较这两条边在重构网络中的概率值P(linkE2)和P(linkEB)，独立比较n次，如果有n1次P(linkE2)>P(linkEB)，有n2次P(linkE2)=P(linkEB)，那么AUC指标值为

2.2实验验证与结果分析

本文在几个真实的网络数据集上实验，比较了不同算法的准确度。实验的数据集包括：空手道俱乐部[23],美国航空网络[24]，线虫的新陈代谢网络[25]和线虫的神经网络[26]。对比算法采用了不同相似度指标，包括：Common Neighbor(CN)指标，Jaccard指标，AA指标，RA指标，PA指标，Local Paths(LP)指标和Katz指标。实验随机选取90%的数据作为训练数据，剩下10%作为测试数据，将不同的算法应用在上述数据集上，计算AUC值的大小。为减小随机因素的影响，将上述实验进行20次，对每种算法得到的AUC取平均值，以比较不同算法的实验效果。

在进行基于非负矩阵分解的网络重构时，需要先对网络数据进行预处理，将各网络视作无权无向，将节点和连边数据转化为元素仅为0和1的邻接矩阵的形式。实验中先设定社团个数k和平衡参数λ为定值，比较基于非负矩阵分解和基于不同相似度的方法得到的重构网络的准确度，然后分别调节参数k和λ的取值大小，讨论其对网络重构效果的影响。

2.2.1基于CNMF和基于不同相似度的网络重构方法比较

在基于相似度的方法中，基于路径信息的指标需要设定权重衰减因子来衡量不同长度路径对相似度的影响。本文实验中LP指标设定参数为0.000 1，Katz指标设定参数为0.01。在CNMF中，社团的个数k是可调参数，此处设定k=16，后文将比较不同的k值对重构效果的影响。链路预测结果如表1所示，虚假边识别结果如表2所示。

表1　CNMF与基于相似度的方法在四种网络上的链路预测结果比较

表2　CNMF与基于相似度的的方法在四种网络上的虚假边识别结果比较

在表1，2中，黑体为不同的算法在该数据上的最大AUC值。可以看出，CNMF和PA指标做链路预测都有很好的效果，仅仅在线虫的新陈代谢网络上CNMF的AUC值低于基于PA指标链路预测的AUC值；另一方面，CNMF做虚假边识别的效果非常好，在4个数据集上的AUC值都比基于相似度指标的算法有很大提高，相比之下PA指标的虚假边识别能力就较差。

2.2.2基于CNMF和RCNMF的网络重构方法比较

由于缺乏足够的先验知识确定社团个数，实验中设置社团的个数取多个值。由于网络一般具有层次性，规模较大的社团内部可能包含有小规模的社团，设定社团的个数为2，4，8，16等以2的指数幂增加。考虑到社团本身包含的节点个数的特征，设定社团个数的上限为网络1/3。进一步地，为综合不同观察尺度下的实验结果，本文将不同层次社团下得到的逼近矩阵结合起来，即将不同k值得到的逼近矩阵相加，作为最终的网络重构矩阵，然后在4个数据集上测试效果。CNMF和RCNMF及其集成算法Integrated CNMF(ICNMF)和Integrated RCNMF(IRCNMF)在不同网络上做链路预测的效果见图1，虚假边识别的效果见图2，其中算法RCNMF和IRCNMF中的平衡参数λ取0.4，后文将比较不同的λ值对重构效果的影响。为作图方便，图1和图2的横坐标均取以2为底，社团个数k的对数，纵坐标为20次实验得到的AUC的平均值，并给出了相应的方差。

观察图1，2中各方法的重构效果，可以发现以下几点：

1) 在karate网络上，AUC值的方差比较大。一方面是由于选取训练集和测试集的随机性可能导致不同的逼近矩阵和测试结果，另一方面是由于该网络本身规模较小，去掉部分连边影响到网络的社团结构，使得重构效果受训练集影响偏大。

2) 除去在karate网络上，随着社团个数k的增加，AUC值均呈现先增大后减小的趋势，即网络重构效果先变好后变差。这是由于k的增加意味着矩阵H和S的维数增加，元素个数增加，有更多的变量去更好的逼近原始观测矩阵，当k值过大时原始矩阵中的观测误差也被很好地逼近，导致其泛化能力降低，即出现了过拟合现象。

3) 无论是链路预测和虚假边识别，加正则化后的RCNMF在多数网络上均优于不加正则化的CNMF。这是由于正则化是对社团隶属度矩阵H的元素的限制，使其保持原始观测矩阵的几何邻近性特征，可以看作先验知识对重构矩阵的修正，故网络重构效果会更好。

4) 无论是链路预测还是虚假边识别，集成算法ICNMF的重构效果在4个网络上均优于原始的CNMF算法，说明综合考虑网络各个层次的结构信息，会有助于对网络拓扑的解释，从而生成更好的重构网络。

5) 对于加正则化的算法而言，集成后的IRCNMF在虚假边识别时效果优于RCNMF，在链路预测时小于RCNMF取不同k值时能得到的最大值，出现后者的原因可能是选取不同k值得到的重构矩阵的集成方式不够合理。没有考虑不同重构矩阵的逼近误差，只是将效果不同的重构矩阵等同对待来集成，导致一些原本较好的重构结果被掩盖。深层次的原因还需要进一步研究。

2.2.3平衡参数λ对RCNMF的网络重构效果的影响

在上述实验中，平衡参数λ固定取值为0.4。实际应用中，参数λ是调节逼近误差项和正则化项对目标函数影响的平衡参数，其取值会影响到算法的性能指标。固定社团个数k为16，参数λ分别取0.04，0.4，4，40，400时，在USAir，Metabolic和C.elegans 3个数据集上进行网络重构实验，来测试λ对重构效果的影响。表3为参数对链路预测的影响，表4为参数对虚假边识别的影响，图3更直观地显示了参数变化对网络重构效果的影响。

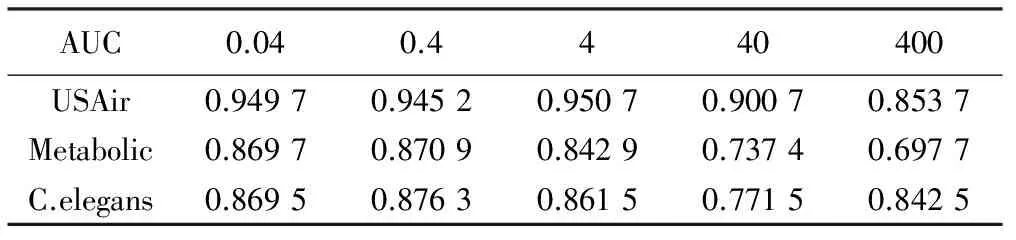
表3　平衡参数对3个网络数据集链路预测效果的影响

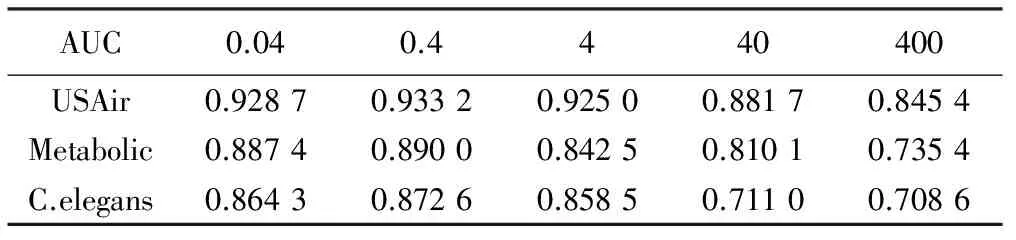
表4　参数对3个网络数虚假边识别效果的影响

在表3，4中，黑体为不同的参数在3种网络数据上的最大AUC值。结合图3可以看出，随着平衡参数λ的增大，网络重构的准确率先增加后减少，且在取值为0.4的时候取得最大值。在λ取值较小时其变化对网络重构的影响很小，能保持在较高的准确率，当λ取值过大时重构准确率下降很快。说明在网络重构的过程中，应优先考虑减少对原始网络的逼近误差，然后是保持节点在划分社团时的几何临近性。

3　总结与展望

针对网络重构问题，本文提出社团结构决定网络连接的假设，基于此假设将网络重构问题转化为非负矩阵分解问题来解决，同时讨论了图正则化和各参数的取值影响，得到了比传统的基于相似度的算法更好地重构效果。该方法对于网络的生成和演化机制的研究具有参考价值。该工作可以拓展到加权网络的重构问题，如何更好地解释权重和连边可能性是下一步的研究方向。如何根据不同观察尺度下得到的逼近误差将重构矩阵进行整合以得到更好的重构效果、社团结构对网络的生成和演化机制产生影响有什么深刻的内在机理，都是值得进一步深入研究的问题。

[1]汪小帆,李翔,陈关荣.网络科学导论[M].北京:高等教育出版社.2012:3-27.

[2]吕琳媛, 陆君安, 张子柯，等. 复杂网络观察[J]. 复杂系统与复杂性科学, 2010, 7(2/3): 173-186.Lü Linyuan, Lu Junan, Zhang Zike, et al. Looking into complex networks [J]. Complex Systems and Complexity Science, 2010, 7(2/3): 173-186.

[3]Albert R, Barabási A L. Statistical mechanics of complex networks [J]. Reviews of Modern Physics, 2002, 74(1): 47-97.

[4]方义，夏承遗，刘子超，等.闪烁小世界网络上疾病传播的动态行为研究[J].复杂系统与复杂性科学，2011, 8(3): 34-37.

Fang Yi, Xia Chengyi, Liu Zichao, et al. Dynamical behavior of disease spreading on blinking small-world networks [J]. Complex Systems and Complexity Science, 2011, 8(3): 34-37.

[5]Xia C Y, Wang Z, Sanz J, et al. Effects of delayed recovery and nonuniform transmission on the spreading of diseases in complex in complex networks [J]. Physica A, 2013, 392, 1577-1585.

[6]Wang X F, Chen G R. Pinning control of scale-free dynamical networks [J]. Physica A, 2002, 310(3/4): 521-531.

[7]吕琳瑗,周涛.链路预测[M].北京：高等教育出版社.2013: 42-56,172-212.

[8]Guimerà R, Sales-Pardo M. Missing and spurious interactions and the reconstruction of complex networks [J]. Proceedings of the National Academy of Sciences, 2009, 106(52): 22073-22078.

[9]Shen Z, Wang W X, Fan Y, et al. Reconstructing propagation networks with natural diversity and identifying hidden sources[J]. Nature Communications, 2014, 5(5):4323.[10] Lü L, Zhou T. Link prediction in complex networks: a survey[J]. Physica A: Statistical Mechanics and Its Applications, 2011, 390(6): 1150-1170.

[11] Liben‐Nowell D, Kleinberg J. The link-prediction problem for social networks[J]. Journal of the American Society for Information Science and Technology, 2007, 58(7): 1019-1031.

[12] Zhou T, Lü L, Zhang Y C. Predicting missing links via local information[J]. The European Physical Journal B-Condensed Matter and Complex Systems, 2009, 71(4): 623-630.

[13] Clauset A, Moore C, Newman M E J. Hierarchical structure and the prediction of missing links in networks [J]. Nature, 2008, 453(7191): 98-101.

[14] Gao S, Denoyer L, Gallinari P. Temporal link prediction by integrating content and structure information [C] //Proceedings of the 20th ACM International Conference on Information and Knowledge Management. Glasgow, Scotland, UK: ACM, 2011: 1169-1174.

[15] Candès E J, Recht B. Exact matrix completion via convex optimization[J]. Foundations of Computational Mathematics, 2009, 9(6): 717-772.

[16] Candès E J, Li X, Ma Y, et al. Robust principal component analysis?[J]. Journal of the ACM, 2011, 58(3): 11-12.

[17] 程学旗, 沈华伟. 复杂网络的社区结构[J]. 复杂系统与复杂性科学, 2011, 8(1): 57-70.

Cheng Xueqi, Shen Huawei. Community structure of complex networks [J]. Complex Systems and Complexity Science, 2011, 8(1): 57-70.

[18] Lee D D, Seung H S. Learning the parts of objects by non-negative matrix factorization [J]. Nature, 1999, 401(6755): 788-791.

[19] Ding C, He X, Simon H D. On the equivalence of nonnegative matrix factorization and spectral clustering[C]// SIAM International Conference on Data Mining. Vancouver, British Columbia, Canada: SIAM, 2005, 5: 606-610.

[20] Ding C, Li T, Peng W, et al. Orthogonal nonnegative matrix t-factorizations for clustering[C]//Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Philadelphia, USA: ACM, 2006: 126-135.

[21] Lee D D, Seung H S. Algorithms for non-negative matrix factorization[C]//Advances in Neural Information Processing Systems. Massachusetts, Cambridge, USA: The MIT Press, 2001: 556-562.

[22] Cai D, He X, Han J, et al. Graph regularized nonnegative matrix factorization for data representation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8): 1548-1560.

[23] Zachary W W. An information flow model for conflict and fission in small groups [J]. Journal of Anthropological Research, 1977: 33(4): 452-473.

[24] Vladimir B, Andrej M. Pajek datasets [DB/OL].[2013-12-30], http://vlado.fmf.uni-lj.si/pub/networks/data/mix/USAir97.net.

[25] Duch J, Arenas A. Community detection in complex networks using extremal optimization [J]. Physical Review E, 2005, 72(2): 027104.

[26] Watts D J, Strogatz S H. Collective dynamics of ‘small-world’ networks[J]. Nature, 1998, 393(6684): 440-442.

(责任编辑耿金花)

Complex Network Reconstruction Based on Nonnegative Matrix Factorization

CHEN Zengqiang1,2, XIE Zheng1, ZHANG Qing2

( 1.Tianjin Key Laboratory of Intelligent Robotics, College of Computer & Control Engineering,Nankai University, Tianjin 300071, China 2. College of Science, Civil Aviation University of China, Tianjin 300300, China )

Based on the hypothesis that community structure determines the network connections, the connection probability matrix which describes the nodes’ community structure can be transfered into the form of product of matrices. The nonnegative matrix factorization is applied here to get the connection probability matrix and then obtain the reconstruction. Experiments on several real world datasets show that the proposed algorithm outperforms some other algorithm which are based on similarity indexes.

complex network; network reconstruction; community structure; connection probability matrix; nonnegative matrix factorization.

1672-3813(2016)03-0026-07;DOI:10.13306/j.1672-3813.2016.03.004

2014-09-05；

2014-11-16

国家自然科学基金(61174094)；天津自然科学基金(14JCYBJC18700，13JCYBJC17400)

陈增强(1964-)，男，天津人，博士，教授，主要研究方向为复杂网络，多智能体系统。

N94

A