空间网络的标度性质对Naming Game演化行为的影响

庄　倩，沈哲思，何　琳，狄增如

(1. 南京农业大学信息科学技术学院，南京 210095； 2. 北京师范大学系统科学学院，北京 100875)



空间网络的标度性质对Naming Game演化行为的影响

庄倩1，沈哲思2，何琳1，狄增如2

(1. 南京农业大学信息科学技术学院，南京 210095； 2. 北京师范大学系统科学学院，北京 100875)

鉴于社会网络结构对于信息传播、共识形成等社会行为的重要影响，在有限能量约束条件下，通过添加距离服从幂律分布的长程连边，构造出具有标度性质的空间网络。在此空间网络上，讨论了引入无意收听机制的Naming Game 模型的演化行为。研究发现，存在一个最优的幂指数，使得该空间网络上的Naming Game 模型收敛时间最短,当能量约束足够大时，这一最优幂指数趋于1.5附近。本研究说明，社会关系网络中的空间性质对于社会集体认同的形成有很大的影响。

空间网络；标度性质；Naming Game；收敛

0　引言

近年来，关于语言的形成与演化已成为人们感兴趣的焦点问题[1]，它关心语言如何产生、以及作为人类交流工具的语言符号如何在个体之间传播扩散并得到认同等[2-3]。20世纪末，Steels提出了一个简单的语言动力学模型——Naming Game模型，用来解释存在交互关系的个体之间如何通过多次互动最终形成集体认同[4]。随着信息网络技术的发展，Naming Game模型有着越来越广泛的应用领域。特别是随着Web 2.0等社会服务网络技术的发展，Delicious、Flickr和CiteUlike等社会标签系统也逐渐发展起来，用户可以通过分享、点赞、评论以及标注等交互行为逐渐对书签、图片、电影等信息资源形成统一的标签共识。因此，社会标签系统的演化过程可以用Naming Game 这样的动力学模型来研究和刻画，而对Naming Game模型的进一步研究则有助于推动社会标签系统的发展。由此看来，无论在理论上还是实际应用上，Naming Game 的研究都很有意义。因此，近二十年来Naming Game模型备受关注，涌现出了大量的研究，尤其是关于在一个群体中语言或约定是如何随着时间的发展而产生和演化的[2-3,5]。已有研究发现，对于Naming Game模型，在没有任何中介协调的情况下，通过个体间局部的成对交互就能使系统达到全局收敛[6-7]。

2005年，Baronchelli等人在原始Naming Game模型的基础上提出了简化模型，这个简化的模型突破了系统规模的限制，从最初的十个扩展到上千个，他们分析了交互成功率随时间的变化模式，并揭示了系统的收敛时间、系统达到最大词汇量的时间以及系统的最大词汇量与参与者的数量存在的幂律关系[8]，更加突出了时间和词汇量等个体交互和共识形成的关键因素。Baronchelli等人的工作是基于在完全图上进行交互的假设，但近年来随着复杂网络研究的发展[9-10]，人们开始了从复杂网络的角度研究Naming Game 模型，分析网络的拓扑性质对系统演化的影响[11-15]。研究表明，基于规则网络的Naming Game中，词汇量相对较小，而收敛时间相对较长[16]；网络的小世界特性则使得Naming Game模型的收敛速度比在规则网络上更快，而在异质网络上，由于度不同的点在演化中所起的作用不同，导致了局部较早达到一致状态，然后由积累了大量词汇的高度节点将词汇传播出去，最终导致系统的全局收敛[17]。除了个体之间交互作用的网络结构方面的研究外，一些人类社会的典型特征也被引入Naming Game模型中，例如有限的记忆[18]、声誉效应[19]、无意间的收听[20]等。

由于结构对系统功能起决定性作用，随着空间网络的发展涌现出一批探讨空间网络结构对系统动力学的影响的研究。Yang等[33]在引入了总能量约束的空间网络上研究了网络的导航问题，探讨了幂指数对网络平均最短路径的影响。Li等[34]在Kleinberg 导航模型中添加了总能量的限制，研究发现导航模型在有限能量约束下的最优导航幂指数为网络维数加一，黎勇等[26]从理论上证明了当网络规模足够大且总能量相对较小时，二维有限能量约束下的最优导航幂指数为 3。除了空间网络上的导航性，学者们也对空间网络上的Ising模型、随机游走、同步能力等动力学过程进行了研究[35]，给出了Ising模型相变的临界温度与网络的空间维度和长程连边的关系[36-38]，随机游走覆盖范围与游走时间的标度关系[39-40]，以及空间网络和小世界特性对网络同步能力的影响[41-42]。同时，也有相关学者研究探讨了社会网络的空间性质对社会行为如疾病传播等的影响[43]。

本文以有限能量约束下的空间网络模型为基础，讨论引入空间地理位置因素后的网络上的Naming Game模型，特别关注空间标度性质对模型收敛行为的影响。此外，现有的社交网络不单单是两两交互，而是多人的交互，例如，微信的朋友圈、微博、QQ空间等，一个用户发出的信息，其所有的好友都可以分享。基于此，我们考察的是引入无意间的收听机制的Naming Game模型。所谓无意间的收听机制，即发话者发出的信息，其所有的邻居都作为接听者可以接收到这个信息。引入这样的机制后的Naming Game模型更容易达到全局收敛[21]。通过对空间网络上这个改进的Naming Game模型的研究，发现存在一个最优的幂指数γ使得该Naming Game模型的收敛时间最短。此外，当能量约束足够大时，使Naming Game 模型收敛最快的最优幂指数γ将趋于1.5附近。同时，我们也研究了系统中最大的不同词汇量和最大总词汇量，与总能量约束和幂指数γ之间的关系，研究发现，给定总能量约束的情况下，存在一个使得系统中最大总词汇量最大的最优γ值。并且，随着总能量的增加，这个最优γ值逐渐趋于2附近。

1　模型

1.1建立二维能量约束下的空间网络

1)N个点被排列在一个周期边界的二维网格上，每个节点与其最近的4个邻居建立短程连接；

3) 随机选择一个节点i，然后在与节点i的距离为r的所有节点中随机选择一个节点j，若节点i和节点j之间没有连接，则在这两个节点之间建立一条长程连边，考虑到能量消耗正比于节点间的距离，假设该长程连边使总能量消耗；

4) 重复步骤2)和3)，直到总能量耗尽。

图1给出了二维有限能量约束下的空间网络的示意图。从构建网络的方式可以看出，空间网络模型中包括两个参数：γ和c。其中参数γ(距离分布的幂指数)能够对空间网络的结构和功能产生决定性的影响。当γ→∞时，距离最短的边出现的概率将趋近于1，而长距离的连边将缺失，在这种情况下，空间网络便与规则网络类似；当γ→0时，不同距离的边出现的概率相等，任意两点之间的连接概率相等，在这种情况下，空间网络便成为一个NW小世界网络[44]。

1.2引入无意收听机制的Naming game模型

在引入无意收听机制的Naming game模型中，上述空间网络中的N=n×n个节点对应着N个智能体，他们可以和任意一个邻居进行交互。这N个智能体对同一个目标制定一个特定的名字，最终形成的“目标-名字”匹配必须得到所有个体的共同认可。每个智能体拥有一个存储库，在这个存储库里，存放着一批不限制优先级的名字。在初始时刻，所有智能体的存储库都是空白的。系统的演化规则即智能体间的交互规则为：

1) 在每个时间步，随机选择一个个体i作为发话者，他所有的邻居作为接听者，发话者i从当前的存储库里随机选择一个名字，如果此时存储库为空，则创造一个新的名字，并将这个名字传递给接听者。

2) 如果接听者j的存储库里有发话者i传递过来的这个名字，那么交互成功，接下来交互双方将各自存储库里的其他名字删除，仅保留刚刚选择的这个名字，只要发话者i的接听者中至少有一个个体与其交互成功，发话者i就将存储库里的其他名字删除，保留交互成功的这个名字。

3) 如果接听者j的存储库里没有发话者i传递过来的这个名字，那么交互失败，接听者将接收到的名字加入自己的存储库。

图2给出了交互过程失败和成功的例子，在图中，选择图1中的节点i作为发话者，他的所有邻居作为接听者，发话者选择的名字用下划线标示。图2a表示失败的交互，当发话者选择B并将其传递给所有接听者时，所有接听者的存储库中没有相应的B，因此交互失败，同时接听者将B增加进自己新的存储库；图2b表示成功的交互，当发话者选择C并将其传递给接听者时，接听者2的存储库拥有相应的C，因此交互成功，发话者和接听者2将自己的存储库中非C的其他字母清空，除接听者2之外的其他的接听者交互失败，将C加进自己的存储库中。

2　模拟结果

在这个Naming Game模型中，系统经过一段时间的演化可以达到所有个体共同认可一个名字即达成共识的稳态。无论对于智能体还是人类来说，在合作和交流中快速达成共识很重要。所以，定义达到稳态的时间为收敛时间tc，它是对系统收敛效率的测量。首先，在规模为100×100的二维网格上构造空间网络。这样的空间网络具有如下特征：在能量约束常数c不变的情况下，随着幂指数γ增加，长程连边的长度越长，出现的概率越小，由于存在总能量约束，因此长程连边的数量将会增加；在幂指数γ不变的情况下，能量约束常数c增加，会使得网络中的连边数量增加。

2.1网络结构对收敛时间的影响

通过模拟分析，首先探讨了长程连边的数量和长度如何影响系统的收敛时间tc。图3给出了规模为100×100的网络上，在取不同的能量约束常数c的情况下，收敛时间tc与幂指数γ之间的关系。从图中很明显地看出，收敛时间tc不是幂指数γ的单调函数。在每个能量约束常数c下，都能找到一个使收敛时间达到最优的γ值γopt。并且随着能量的增加，γopt逐步接近于1.5，幂指数1.5对应的空间网络具有最大的输运能力[33]，这样的网络结构有利于信息的传播，增加了收敛速度。这部分结果说明网络结构对于最优结果的形成是有很大影响的。此外，从图3中还可以看出，总能量越大，系统的收敛时间越短。这也说明长程连边的数量越多越有利于全局收敛。

2.2网络结构对不同词汇量的影响

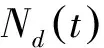
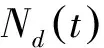
2.3网络结构对总词汇量的影响

3　结论与展望

本文首先建立了二维有限能量约束下的空间网络，并在此二维空间网络上讨论了一个引入无意收听机制的Naming Game模型，在此基础上，细致研究了空间网络的标度性质对模型演化行为的影响。我们发现存在一个距离分布的最优幂指数γ，使得该空间网络上的Naming Game 模型收敛时间最短。进一步，我们从总能量约束的角度讨论了空间网络结构对该最优幂指数γ的影响。研究结果表明，当能量约束足够大时，使得Naming Game 模型收敛最快的最优幂指数γ最终将稳定在1.5附近，对应的空间网络具有最大的输运能力。这个结果说明，适当远距离的交流能够促进集体认同的快速形成。局部近距离的交流或者是全局的交流都不利于甚至是阻碍集体认同的形成。同时，我们还研究了总能量约束和幂指数γ对系统中最大的不同词汇量和最大词汇量的影响。结果发现，随着总能量的增加，最大词汇量的峰值对应的γ值在不断减小，说明远距离的交流需要更大的存储空间，即更高的记忆能力。但当能量约束足够大时，对应最大词汇量峰值的γ值稳定在2左右，此时空间网络具有最小的平均最短路径。

综上所述，空间结构性质是社会关系网络普遍存在的性质，而它所展现出来的标度性质对许多社会行为有重要影响。本文的工作一方面丰富了网络上Naming Game模型的研究；更重要的是从更符合现实的角度对Naming Game模型进行了研究和改进，并特别关注了社会网络空间结构性质对模型收敛行为和最终稳态的影响。当然，在这一研究领域可待研究的问题还有很多，例如，结合社会标签系统的演化规律改进Naming Game模型，使其能够更好地模拟现实，从而进一步揭示人类集体认同的形成。这样的研究不但对于研究语言形成问题，而且对于研究社会惯例、文化的产生和演化、及其与空间地域性质之间的相关关系也有很大的理论意义和实际价值。

[1]潘向东,杨建梅.Naming Game模型的研究进展及应用[J].复杂系统与复杂性科学, 2009, 6(2): 87-92.

Pan Xiangdong, Yang Jianmei. A survey of the development and application of Naming Game model [J]. Complex Systems and Complexity Science, 2009, 6(2): 87-92.

[2]Steels L.The synthetic modeling of language origins[J].Evolution of Communication, 1997, 1(1): 1-34.

[3]Kirby S. Natural language from artificial life [J]. Artificial Life, 2002, 8(2): 185-215．

[4]Steels L. A self-organizing spatial vocabulary[J]. Artificial Life, 1995, 2(3): 319-332．

[5]Lu Q, Korniss G, Szymanski B K. Naming games in two-dimensional and small-world-connected random geometric networks[J]. Phys Rev E, 2008, 77: 016111.

[6]Briscoe T. Linguistic Evolution Through Language Acquisition: Formal and Computational Models[M]. Cambridge: Cambridge University Press,2002.

[7]Hurford J, Knight C, Studdert-Kennedy M. Approach to the Evolution of Human Language[M]. Cambridge: Cambridge University Press,1999.

[8]Baronchelli A, Felici M, Caglioti E, et al. Sharp transition towards shared vocabularies in multi-agent systems[J]. Stat Mech, 2005, 6014: 0509075.

[9]Dorogovtsev N, Mendes J F F. Evolution of Networks: from Biological Nets to the Internet and WWW[M]. Oxford: Oxford University Press, 2003.

[10] Pastor-Satorras R, Vespignani A. Evolution and Structure of the Internet: a Statistical Physics Approach[M]. Cambridge: Cambridge University Press, 2004.

[11] Gao Y, Chen G R, Chan R H M. Naming game on networks: let everyone be both speaker and hearer [J]. Scientific Reports, 2014, 6:149.

[12] Dall’Asta L, Baronchelli A, Barrat A, et a1．Agreement dynamics on small-world networks [J]. Europhys Lett, 2006, 73: 969.

[13] Barrat A, Baronchelli A, Dall’Asta L, et al. Agreement dynamics on interaction networks with diverse topologies [J]. Chaos, 2007, 17: 026111.

[14] Baronchelli A, Dall’Asta L, Barrat A, et al. The role of topology on the dynamics of the Naming Game [J].EurPhys J Special Topics, 2007, 143: 233-235.

[15] Liu R R, Wang W X, Lai Y C, et al. Optimal convergence in naming game with geography-basednegotiation on small-world networks [J]. Phys Lett, 2011, 375: 363-367.

[16] Baronchelli A, Dall’Asta L, Barrat A, Loreto V. Topology-induced coarsening in language games[J]. Phys Rev E, 2006, 73: 015102(R).

[17] Dall’Asta L, Baronchelli A, Barrat A, et al. Nonequilibrium dynamics of language games on complex networks [J]. Phys Rev E, 2006, 74: 036105.

[18] Wang W X, Lin B Y, Tang C L, et al. Agreement dynamics of finite-memory language games on networks [J]. Eur Phys J B, 2007, 60: 529-536.

[19] Brigatti E. Consequence of reputation in an open-ended naming game[J]. Phys Rev E, 2008, 78: 046108.

[20] Maity S K, Mukherjee A, Tria F, et al. Emergence of fast agreement in an overhearing population: the case of the naming game [J]. Euro Phys Lett, 2013, 101(6): 68004.

[21]Liben-Nowell D, Novak J, Kumar R, et al. Geographic routing in social networks [J]. Proc Natl Acad Sci USA, 2005, 102(33): 11623-11628.

[22] Adamic L, Adar E．How to Search a Social Network [J]. Social Networks, 2005, 27(3): 187-203.

[23]Lambiotte R, Blondel V D, De Kerchove C, et al, Geographical dispersal of mobile communication networks [J]. Physica A, 2008, 387: 5317-5325.

[24] Yook S H, Jeong H, Barabási A L. Modeling the Internet's large-scale topology [J]. Proc Natl Acad Sci USA, 2002, 99: 13382-13386.

[25]黎勇,胡延庆,张晶,等. 空间网络综述[J].复杂系统与复杂性科学, 2010, 7(2/3): 145-163.

Li Yong, Hu Yanqing, Zhang Jing, et al.Review on spatial networks[J]. Complex Systems and Complexity Science, 2010, 7(2/3): 145-163.

[26] 钭斐玲,胡延庆,黎勇,等.空间网络上的随机游走[J].物理学报, 2012, 61(17): 571-577.

Dou Feiling, Hu Yanqing,Li Yong, et al. Random walks on spatial networks [J]. Acta Physica Sinica, 2012, 61(17): 571-577.

[27] 黎勇,钭斐玲,樊瑛,等.二维有限能量约束下最优导航问题的理论分析[J].物理学报, 2012, 61(22): 546-551.

Li Yong,Dou Feiling, Fan Ying, et al.Theoretical analysis on optimal navigation with totalenergy restriction in a two-dimensional lattice [J]. ActaPhysicaSinica,2012, 61(22): 546-551.

[28] Viswanathan G M, Buldyrev S V, Havlin S, et al. Optimizing the success of random searches [J]. Nature, 1999, 401: 911-914.

[29] Viswanathan G M,AfanasyevV, Buldyrev S V, et al. Levy fights in random searches [J]. Physica A, 2000, 282: 1-12.

[30] Brockmann D, Hufnagel L, Geisel T. The scaling laws of human travel [J]. Nature, 2006, 439: 462-465.

[31] Shlesinger M F. The structure of suspended graphene sheets [J]. Nature, 2006, 2: 60-63.

[32] Gonzalez M C, Hidalgo C A, Barabási A L. Understanding individual human mobility patterns [J]. Nature, 2008, 453: 779-782.

[33] Yang H, Nie Y C, Zeng A, et al. Scaling properties in spatial networks and their effects on topology and traffic dynamics [J]. Euro Phys Lett, 2010, 89: 58002.

[34] Li G, Reis S D S, Moreira A A, et al． Towards design principles for optimal transport networks [J]. Phys Rev E, 2010, 104: 018701.

[35] Barthélemy M. Spatial networks [J]. Physics Reports, 2011, 499: 1-101.

[36] Barrat A, Weigt M. On the properties of small-world network models [J]. Euro Phys J B, 2000, 13: 547.

[37] Barthélemy M, Flammini A. Optimal traffic networks [J]. J Stat Mech, 2006, L07002.

[38] Bradde S, Caccioli F, Dall’asta L, et al. Critical fluctuations in spatial complex networks [J]. Phys Rev Lett, 2010, 104: 218701.

[39] Jespersen S, Sokolov I M, Blumen A. Relaxation properties of small-world networks [J]. Phys Rev E, 2000, 62: 4405-4408.

[40] Monasson R. Diffusion, localization and dispersion relations on small-world lattices [J]. Euro Phys B, 1999, 12: 555-567.

[41] Chowdhury D, Cross M C. Synchronization of oscillators with long range power law interactions [J]. Phys Rev E, 2010, 82:016205．

[42] Zeng A, Zhou D, Hu Y Q, et al. Dynamics on spatial networks and the effect of distance coarse graining [J]. Physica A, 2011, 390(2122): 3962-3969.

[43] Murray J D. Mathematical Biology[M]. New York: Springer， 1993： 315-379.

[44]Newman M E J, Watts D J. Renormalization group analysis of the small-world network model [J]. Phys Lett A, 1999, 263: 341-346.

[45] 汪小帆, 李翔, 陈关荣. 网络科学导论[M].北京: 高等教育出版社, 2012.

(责任编辑李进)

Effects of Geographic Scaling Property on the Evolution of Naming Game

ZHUANG Qian1, SHEN Zhesi2, HE Lin1, DI Zengru2

(1.College of Information Science and Technology, Nanjing Agricultural University, Nanjing 210095, China;2. School of Systems Science, Beijing Normal University, Beijing 100875, China)

The structure of social networks is of paramount importance in collective behaviors，e.g. information propagation, consensus and formation of social norms. In this paper, a special network is constructed by adding remote links among nodes over lattice graphs with total energy constraints.A power law distribution is used to model the relation between the link probability and the distance.We study the effect of geographic scaling property on the dynamics of Naming Game with a group interaction rule. We find that there exists an optimal parameter value which minimizes the time to converge to global consensus. When the total energy constraint is large enough the optimal parameter value is approximately 1.5. Numerical simulations indicate that the geographic scaling property in social network plays an important role in the emergence of social collective behavior and rules.

spatial networks； scaling property； Naming Game； convergence

1672-3813(2016)03-0019-07；DOI:10.13306/j.1672-3813.2016.03.003

2015-03-03；

2015-05-21

国家社会科学基金(14CTQ044)；国家自然科学基金(70974084, 61174150)；北京市优秀博士学位论文指导教师科技项目(20121002704)

庄倩(1984-)，女，黑龙江肇东人，博士，讲师，主要研究方向为复杂系统的演化机理。

N94

A