电视节目竞争关系的超网络分析

索　琪，郭进利，王福红a

(1.上海理工大学a.管理学院,b. 超网络研究中心，上海 200093；2. 青岛科技大学经济与管理学院，山东 青岛 266061)



电视节目竞争关系的超网络分析

索琪1a,2，郭进利1，王福红1a

(1.上海理工大学a.管理学院,b. 超网络研究中心，上海 200093；2. 青岛科技大学经济与管理学院，山东 青岛 266061)

给出了超网络中点度、点超度、加权点度、边度、超边度、聚集系数、平均距离等拓扑特性的定义和计算公式。将电视节目定义为节点，将播出时间段定义为超边，采用超网络方法分析了电视节目的竞争关系。实证结果显示，这些统计属性的累计概率分布服从指数分布，说明多个随机因素的相互作用导致了该超网络的形成。其中，加权点度能够更好地描述超网络的竞争态势。较小的平均距离和较大的聚集系数表明该超网络符合小世界效应。这些拓扑指标能够较好地反映竞争超网络所具有的特点，方法同样适用于实证分析其它合作或竞争超网络。

复杂网络；超图；超网络；拓扑特性

0　引言

近年来复杂网络的研究引起了学者的广泛关注。在许多实际问题中，可以把复杂系统单元之间的相互作用关系简化表示为图论中节点以及连接节点的边的集合，这为复杂系统的建模提供了新的尝试。1998年，Watts和Strogats提出了WS模型[1]，1999年Barabasi和Albert提出了无标度网络的BA模型[2]，发现了实际网络区别于规则网络与随机网络的普遍性质，引发了复杂网络研究的热潮。随后，复杂网络的研究涉及到通讯、物理、信息、交通、生物等各个领域。大量学者研究了网络的静态拓扑属性，并在此基础上构造了网络模型, 提出了许多分析模型的方法[3]。

社会网络研究中的合作和竞争网络，一直被认为是研究的重点。这类网络研究常用二分图描述，网络中存在两类节点，一类节点称之为“项目”(act，如科研项目)，另一类节点称为“参与者”(actor，如科研人员) 。两类节点间的一条边代表一个参与者参加一个合作项目[4-5]。由于二分图中两类节点的异质性，且每条连边只能关联两个节点。研究同一类节点之间的相互作用关系是我们所关心的重点，如科研人员在项目中的合作关系，因此常把二分图的边向同一类节点投影，得到投影图。但随着网络化的发展, 节点和连边数量剧增，连边类型的多样化、结构的复杂性，使得复杂网络无法全面有效地描述现实网络的特征。Berge[6]给出了超图理论的基本概念和性质，由于超图中的一条超边可以包含多个节点，能够更好地描述现实系统。因此，基于超图理论的超网络可以很好地描述各个节点之间的相互作用和影响。越来越多的学者将研究视角转向用超网络方法刻画现实网络这一领域。

近年来, 有学者对超网络的拓扑特征进行了研究。Estrada等[7]研究了超网络的子图中心度和聚集系数问题。Ghoshal等[8]研究了随机三部超图及其应用。Zlatic等[9]分析了基于三部超图模型的统计特性。倪子建等[10]提出以超网络模型描述维基内容本体，对网络的重要拓扑属性进行了分析。王建伟等[11]给出了点度分布、聚类系数、平均距离等拓扑属性的定义。胡枫等[12]构建了一种超网络动态演化模型，并介绍了这个模型的一些基本拓扑性质。目前虽然有学者对于超网络模型中的一些基本拓扑指标给出了定义，但对加权点度、平均距离、聚类系数等重要指标尚未形成统一的定义和计算方法。因此，在其他学者的研究基础上，本文拟将复杂网络的基本拓扑指标推广到超网络中。由于复杂网络可以视为超网络中的一个特例——2-均齐超网络(即每条超边只关联两个节点)。因此，定义和计算的基本原则是，一方面应该反映出超网络中的每条超边可以包含任意个节点这个不同于复杂网络的特性；另一方面当每条超边只包含两个节点时，定义应该可以退化到复杂网络。此外，国内外文献中鲜有结合统计特性来进行超网络的实证研究。

大多数情况下，实际参与同一项目的多个参与者之间普遍存在着竞争关系[13]，以中央电视台的15套节目频道为例，为抢占收视率市场，在同一时间段播出的电视节目之间存在着激烈的竞争关系。本文在描述超网络拓扑特性的指标的基础上，结合央视数据进行实证分析，电视节目超网络属于典型的竞争超网络，定量化研究这种竞争关系，可以更好地描述超网络中节点间的竞争态势。

1　超网络概念及拓扑特性

1.1超网络的概念

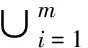
采用不同方法描述复杂系统，可以分别得到二分图、投影图和超图。V代表参与者节点，T代表项目节点，图1a描述了6个参与者参与5个项目的合作关系；图1b描述了6个参与者之间的两两合作关系；图1c中将每个项目看作1条超边，描述了多个参与者同时参与项目的关系。可见，超图可以更好地描述现实系统。

1.2超网络的拓扑特性

1) 点度

超网络中，节点与节点通过超边连接。节点i的点度Di定义为与i直接邻接的节点个数。如在图1c中，Dv1=3,Dv3=4。

2) 加权点度

在计算节点i的点度时仅考虑与该节点直接邻接的节点个数，而未考虑到邻接节点的强度。将节点i与节点j的权值Wij定义为同时包含节点i与节点j的超边数量。则节点i的加权点度Si为

(1)

Ni为节点i的邻接节点集合。如在图1c中，v3,v5同时出现在超边E1,E3中，则Wv3v5=2，而Wv3v1=1,Wv3v4=1,Wv3v6=1，因此，Sv3=5。

3) 点超度

节点i的点超度DHi表示包含该节点的超边条数。如在图1c中，DHv1=2,DHv3=2,DHv6=3。

4) 超边度

超网络中，同一节点可能在多条超边中出现。超边度DEi定义为与超边Ei直接邻接的其它超边条数。如在图1c中，v5同时属于超边E1,E3,E5，则E1,E3,E5是邻接的，v4同时属于超边E1,E2,E4，则E1,E2,E4是邻接的，DE1=4,DE5=2。

5) 超边超度

超边Ei的超边超度DHEi表示该超边所包含的节点个数。如在图1c中，DHE1=4,DHE3=3。

6) 平均距离

在超网络中，节点i与节点j的距离Dij定义为连接i和j的最短路径上的超边数目，即i与j相连所需通过的最少超边数。如在图1c中，节点v1到节点v6的一条最短路径为v1E1v4E4v6，则Dv1v6=2。N为超网络中的节点数量，平均距离描述了节点间的连通程度。超网络的平均距离〈D〉为

对于m-均齐超网络

(2)

对于无自连超网络

(3)

对于一般超网络

(4)

由于式(4)中分母以指数函数形式增长，因此计算出的平均距离〈D〉值较小，为更好地描述超网络中节点的连通程度，定义一般超网络的网络效率E为

(5)

7) 集聚系数

平均聚集系数是指在超网络中与同一节点连接的两个节点之间通过超边也相互连接的平均概率，该系数用于刻画超网络的局域结构性质。

假设节点i与Di个节点通过超边直接相连，Di个节点间实际存在的超边数为Mi，这Di个节点间可能存在的最大超边数为Di(Di-1)/2，由此定义节点i的聚集系数Ci为

(6)

复杂网络的“集聚”可以认为是由一些“三角形连接”组成的。对于超网络而言，“集聚”认为是由一些“超三角形连接”组成的。一个超三角形是指由3个不同的节点和3个不同的超边组成的序列[7]，如在图1c中，v1E1v3E3v5E5v1是一个超三角形，而v1E1v3E3v5E1v1由于存在相同超边，因此不是超三角形。定义2路为长度为2的路，即由3个不同节点和两个不同的超边构成的序列，如v1E1v3E3v5是一个2路。因此，节点i的聚集系数Ci也可以定义为

(7)

其中，NiΔ为与节点i相连的“超三角形”数目，NiΛ为与节点i相连的“2路”数目。

超网络的平均聚集系数为

(8)

2　数据来源及描述

中国中央电视台(China Central Television，CCTV)是中国官方电视媒体之一，拥有最多的收视人群。目前开播15套中文电视节目，节目内容覆盖各个领域，收视群体覆盖各地区、各年龄段的广大人群。近年来电视节目竞争日趋激烈，由于不同频道在同一时段会播放不同的电视节目，各个节目凭借其精彩的内容争夺观众收视率市场，因此同一时段播出的各个节目之间存在竞争关系。数据来源于中央电视台官方网站(http://cctv.cntv.cn，http://tv.cntv.cn/epg)，数据收集时间为2014年4月30日。该网站可以按播出日期、频道搜索各节目的播出时间。由于每个时间段播出的电视节目数量、内容存在较大差异，从而影响该时间段的电视节目的收视率，因此需要对不同时间段进行分析。研究发现，每周播出的电视节目相对稳定，因此以周为单位可以更完整地分析电视节目编排的整体特点。为方便统计，以2 h为一单位对每天的播出时间离散化处理，分段初始点从周一0点开始，结束点为周日的22点，一周共分为84个播出时间段。实证分析包含了15个中文频道的227个播出时间相对稳定的节目数据。

用超网络描述央视电视节目系统，将播出时间段定义为超边，则该超网络含有84条超边；将电视节目定义为节点，则含有227个节点。电视节目在某个时间段播出，则称该节点包含于该超边中。以《新闻联播》节目为例(http://cctv.cntv.cn/lm/xinwenlianbo/20140430.shtml)，其首播时间为每天的19∶00，重播时间为每天的21:00，则其对应的节点包含在所属时间段对应的14条超边中。分析发现，227个节目中有122个只有首播，没有重播；其余105个节目会重播，且重播的总次数达到494，约占总播出次数的1/3左右。因此，重播的节目也是整体节目编排的一个重要组成部分，在初始超网络构建时不区分首播和重播时间的影响，在3.6节中将进一步分析节目重播时间的选取特点。此外，除《新闻联播》等5个新闻类节目在CCTV1综合频道和CCTV13新闻频道同时播出外，其余节目均以独播频道播放。因此，文中忽略同一节目在不同频道播放时对收视率的影响。由于很多电视节目会在不同时间段播出，导致超边会连接起来，构成了本文讨论的电视节目超网络。

3　电视节目超网络的统计分析

3.1点度分布

如果两个节目在同一时段内播出，则它们属于同一超边，表示两个节目在一个特定时间段内的竞争关系。点度的大小反映了与该节目具有竞争关系的节点数目。统计结果显示，平均点度为43.5。其中点度最大的节目为《新闻联播》，点度值为127，该节目的播出时间为周一到周日的19点，由于其每周播出7次，且每天在黄金时段播出，必然导致与该节目竞争的节点数目较多。其中点度最小的节目为《人口》，点度值为5，其播出时间为每周二的2点，由于其每周仅播出1次，且在凌晨时间播出，必然导致与该节目竞争的节点数较少。

点度累计概率分布如图2所示，对曲线拟合发现其服从分段指数分布，拟合的指数函数分别为

(9)

3.2加权点度分布

点度仅反映与该节目具有竞争关系的节点个数，而未考虑到竞争强度。由于每个节目平均每周播放6.5次，导致节目之间会在不同时间段内出现多次竞争现象，将权值Wij定义为同时包含节目i与节目j的时段个数，则加权点度Si可以表示出节目i与其它节目的竞争总次数。结果显示，平均加权点度为114.8，即每个节目每周平均与其它节目发生114.8次竞争。该值较大，原因在于很多电视节目每周在不同时段播出多次，而每个时段中又包含很多节目。显然，加权点度包含比点度更多的信息。

加权点度累计概率分布如图3所示，拟合的指数函数为

y=1.093 9e-0.009 5x(R2=0.988 2)

(10)

3.3点超度分布

点超度的大小反映了一个节目在一周内的播出次数，表明该节目在电视节目超网络中的竞争力大小。统计结果表明，平均点超度为6.5，即平均每个节目每周播放6.5次。从数据看，45个节目每周只播出一次，且非黄金时间的节目编排变化较大。43个节目每周播出七次，且每天在相对固定的时间段播出。还有部分节目因其内容比较精彩，受视面广，一周多次播出，导致其点超度值比较大。

点超度的累计概率分布如图4所示，拟合的指数函数为

y=1.250 8e-0.175 3x(R2=0.983 3)

(11)

3.4点度、加权点度和点超度之间的关系

点超度对应于每个节目的播出次数，点度对应于与该节目有竞争关系的节点数目，加权点度对应于与该节目有竞争关系的节点竞争总次数。三者都反映了节目的竞争力，三者是否存在一定的关联呢？图5 所示，点度和点超度是正相关的，加权点度和点超度也是正相关的。说明当节点在多个时段内播出时，此节点具有更大的竞争力。节目播出次数越多，则与其竞争的节目数量和竞争总次数都会越多。研究其统计关系可知，虽然点度和加权点度均能描述超网络中的这种竞争关系和结构，但用加权点度能更准确地描述超网络的竞争结果。

3.5超边度分布

如果两个节目在同一时间段播出，则其通过超边连接。统计结果显示，平均超边度为54。其中超边度最大的时间段为周二的18～20点，超边度为79，由于黄金时段内的节目数量较多，很多节目也会在其它时段播出，必然导致超边度较大。超边度最小的时间段为周一的2～4点，超边度为26，由于凌晨时段内的节目数量较少，必然导致超边度较小。

超边度累计概率分布如图6所示，对曲线拟合发现其服从分段指数分布，拟合的指数函数分别为

(12)

3.6超边超度分布

超边超度的大小即同一个时间段内播出多少个电视节目，粗略表明了不同时间段的竞争力大小。显然，超边超度越大，竞争越激烈。如图7a所示，通过对一周的节目分析发现，每天的不同时段内的节目数量变化规律基本一致。平均超边超度为17.6，说明平均每个时间段内有17.6个节目播出。超边超度最大的时间段为周五20～22点，超边超度值为32，该时段节目数量达到图中最高点。由于下一天是周末，大量工作的人会选择休闲在家，适宜的节目编排可以引发收视高峰，因此该时段竞争激烈。超边超度最小的时间段为周一的2～4点，超边度为4。由于通宵时间是收视率最低的时段，这个时段节目数量达到最低，进一步分析节目内容，大部分是重播节目。从超边超度的变化趋势看，每天的6～8点清晨时段节目数量达到一个小高峰，这一时段的节目板块以满足观众的信息需求为主；8～12点主要播放生活服务类节目，基本针对白天比较空闲的家庭主妇和老年人；中午的午休时间制造了一个小高峰，以新闻、信息等节目为主；黄昏时段的受众定位于青少年儿童；18～22点为收视黄金时段，节目播出数量逐步达到高峰。

超边超度的累计概率分布如图8所示，对曲线拟合发现其服从分段指数分布，拟合的指数函数分别为

(13)

为进一步分析电视节目编排的整体特点，基于节目的首播时间进行了统计，得到同一时间段首播的电视节目数量，如图7b所示，总体来讲，呈现和图7a类似的趋势。进一步对比发现，每天的18～22点重播的节目数量最少，说明在收视黄金时段，为抢占收视率，各节目都以全新的内容去吸引观众；而每天的0～2点，6点～10点重播的节目数量较多，且6～10点重播的节目内容基本为新闻、健康、科普类节目。

3.7度分布及超度分布的特征描述

由统计结果可知，电视节目超网络的点度、加权点度、点超度、超边超度的累计概率分布都可以很好的用指数分布拟合。由指数分布的性质可知，大部分节点的连接数目大致相同，连接数目比平均数高很多或者低很多的节点极少存在，差别不像幂律分布那样明显。这说明电视节目网络中的节目编排相对均匀，总体上能较好地满足观众的收视需求。

当节点之间的连接完全随机时，网络的演化呈指数分布，这意味着电视节目超网络的演化过程中有很多随机因素。电视节目在进行编排时，在分析电视受众的特征、收视的时间规律及收视内容偏好的基础上，需要在内容和时间上进行整合。在实践中，不仅要考虑单个节目的竞争优势，还要考虑与相邻时段的节目的相适性，有效整合各种电视资源以形成频道的竞争优势。目的是在最合适的时间播出最佳的内容呈现给最需要的受众。从播出时间上，根据特定观众的收视习惯，日播节目一般安排在每天同一时间，以培养相对稳定的收视群体。区别于日播节目，周播的节目主要集中在周末播出，内容则更侧重娱乐性和参与性，这样可以开拓周末的收视空间，符合观众周末愿意看一些视野开阔、轻松娱乐节目的需求。从播出内容上，晨间和中午一般会播放新闻及信息服务类节目；上午一般重播前一天晚上的精彩节目或以老年人为目标受众的节目；下午二至四点播放专业性较强的节目；四至六点播放少儿、学生节目；一些名牌、重点节目会在黄金时段播出；深夜播出情感类访谈节目或重播节目。为增大节目的影响力，很多节目会进行重播，但重播时间都会避开黄金时间。采取差异化的节目编排策略，可以全天候满足不同观众不断变化的收视需求。由于需要考虑的具体因素较多，互相又缺乏关联，相当于随机选取，这应该是大部分竞争网络的共同特征。反之，如果电视节目超网络的分布符合幂律分布，则说明该超网络存在较多弊端，如出现很多节目在一个时段播出或很多时段没有节目播出的情况，这是不符合实际的。

3.8平均距离

实证发现，电视节目超网络的直径为4。平均距离描述了超网络中节点间的平均分离程度，根据2-均齐超网络的计算公式，平均距离为1.8，也就是说平均每个节目只需要经过不到2条超边就能和其它任何一个节目联系起来，这符合小世界效应。根据一般超网络中的效率计算公式，电视节目超网络的效率为49.5。

3.9聚集系数

超网络共有节点227个，超边84条，网络密度很大，节点之间联系紧密。该网络的平均聚集系数为0.69，表明该超网络聚类性质很高，兼具小世界效应。有34个节目的聚集系数为1，这些节目每周只播出一次，与其同时播出的节目相对固定，因此构成大的聚集系数。相反，聚集系数最小的值为0.32，为《新闻联播》，由于该节目在黄金时段播出，且每周多次播出，而每个时段播出的节目数量和内容都有较大差异，导致聚类系数较小。

4　结论

本文以中央电视台15套频道的电视节目数据为例，将电视节目定义为节点，将播出时间段定义为超边，构造了电视节目超网络，该方法可以有效刻画出超网络中的参与者在各个项目中的竞争关系。我们得到了该超网络的点度、点超度、加权点度、边度、超边度等几种统计性质。实证结果显示，这些统计属性的累计概率分布均服从指数分布，说明多个随机因素导致了该超网络的形成。节目编排相对均匀，总体上能较好地满足观众的收视需求。平均距离和聚集系数指标同样适用于描述超网络的连通和聚集程度。以上研究表明，在超图基础上研究竞争超网络的拓扑特性是可行的，文中提出的指标和方法也可用于实证分析其它合作或竞争网络。

未来研究工作将进一步探讨超网络的描述方法，并在此基础上分析其动态演化机理。

[1]Watts D J, Strogatz S H. Collective dynamics of ‘small-world’ networks [J]. Nature, 1998, 393(6684): 440-442.

[2]Barabási A L, Albert R. Emergence of scaling in random networks [J]. Science, 1999, 286(5439): 509-512.

[3]郭进利. 复杂网络和人类行为动力学演化模型 [M].北京: 科学出版社，2013.

[4]Wasserman S, Faust K. Social Network Analysis: Methods and Applications [M]. Cambridge: Cambridge University Press, 1994.

[5]Ramasco J J, Dorogavtsev S N, Pastor-Satorras R. Self-organization of collaboration networks [J]. Physical Review E, 2004, 70(3): 036106.

[6]Berge C . Graphs and hypergraphs [M] .New York: Elsevier, 1973.

[7]Estrada E, Rodríguez-Velázquez J A. Subgraph centrality and clustering in complex hyper-networks[J]. Physica A, 2006, 364: 581-594.

[10]倪子建, 荣莉莉, 刘泉. 基于超网络的维基百科内容知识本体演化研究[J]. 管理科学学报，2013, 16(12): 68-78.

Ni Zijian, Rong Lili, Liu Quan. Study on evolving hypernetwork model of Wiki ontology[J]. Journal of Management Sciences in China, 2013, 16(12): 68-78.

[11]Wang J W, Rong L L, Deng Q H, et al. Evolving hypernetwork model [J]. The European Physical Journal B, 2010,77(4): 493-498.

[12]胡枫, 赵海兴, 马秀娟. 一种超网络演化模型构建及特性分析[J]. 中国科学，2013, 43(1): 16-22.

Hu Feng, Zhao Haixing, Ma Xiujuan. An evolving hypernetwork model and its properities[J]. Scientia Sinica, 2013, 43(1): 16-22.

[13]Jiang Jifa, Cheng Zhixin. The complete strategic classification for a cooperation-competition model in the WWW market [J]. Physical A, 2006, 363 (2): 527-536.

[14]Denning P J. What is computer science?[J]. American Scientist, 1985, 73(1): 16-19.

[15]Estrada E, Rodriguez-Velazquez J A. Subgraph centrality in complex networks[J]. Physical Review E, 2005, 71(5): 056103.

[16]王众托. 关于超网络的一点思考[J]. 上海理工大学学报，2011，33(3): 229-237.

Wang ZhongTuo. Reflection on supernetwork[J]. J. University of Shanghai for Science and Technology, 2011, 33(3):229-237.

(责任编辑耿金花)

The Hypernetwork Analysis of the Television Programs Competitive Relationships

SUO Qi1a, 2, GUO Jinli1, WANG Fuhong1a

(1. a.Business School, b.Center for Supernetwork Research University of Shanghai for Science and Technology, Shanghai 200093， China;2. School of Economics and Management, Qingdao University of Science and Technology, Qingdao 266061， China)

The node degrees, weighted node degrees, node hyperdegrees, hyperedge degrees, hyperedge hyperdegrees, average distance and clustering coefficient are proposed in the paper. TV programs are defined as nodes and broadcasting time periods are defined as hyperedges. By using hypernetwork analysis of television programs competitive relationships, we find that the cumulative probability distributions can be described by an exponential distribution. It shows that random factors result in the formation of the hypernetwork. The competition of the supernetwork can be better described by weighted node degrees. The average distance is small and the clustering coefficient is large. These parameters conform to the characteristics of small-world network. These topological characteristics may be useful for the studies of competitive hypernetworks. The methods proposed can also be used for other empirical studies.

complex network;hypergraph;hypernetwork;topological characteristics

1672-3813(2016)03-0033-07；DOI:10.13306/j.1672-3813.2016.03.005

2014-06-13；

2014-08-12

国家自然科学基金 (71571119)；国家统计科学研究项目(2015LZ249)；山东省统计科研重点课题(KT15059)

索琪(1980-)，女，黑龙江哈尔滨人，博士研究生，讲师，主要研究方向为复杂网络、超网络。

郭进利(1960-)，男，陕西西安人，博士，教授，主要研究方向为复杂网络、人类行为动力学。

T94

A