基于超网络的作战信息流转建模及特性分析

杨迎辉，李建华，王　刚，南明莉,2

(1.空军工程大学信息与导航学院，西安 710077；2.中国人民解放军95881部队，北京100095)



基于超网络的作战信息流转建模及特性分析

杨迎辉1，李建华1，王刚1，南明莉1,2

(1.空军工程大学信息与导航学院，西安 710077；2.中国人民解放军95881部队，北京100095)

针对现有单一要素模式的信息网络不能有效反映作战信息流转复杂结构及动态过程的问题，提出一种基于超网络的作战信息流转“两层三网”模型构建及特性分析方法。首先，分析作战信息流转超网络结构特征，抽象作战节点和信息关系的多维属性，定义关联映射规则，建立作战信息流转超网络模型；其次，从节点的超度分布、超边的度分布、介数、聚类系数、子图向心性和网络弹性6个方面，研究了作战信息流转超网络的拓扑特性。最后，以空中突击作战为例，通过仿真实验，验证了模型与方法的可行性和合理性。

作战；信息流转；超网络；关联映射；拓扑特性；子图向心性；网络弹性

0　引言

现代战争是典型的复杂巨系统，敌对双方的对抗已不仅仅是建制对抗、单元独立对抗，而是整体对抗、体系集成对抗，战场的每一方都是大量作战单元以特定方式耦合的动态网络，作战行动也不再是基于集合的，而是基于网络的。作为作战活动的核心资源和主导因素，信息贯穿体系作战全过程，信息流引导物质流、释放能量流，信息链支持指挥链、控制打击链，信息流转在战场资源调控、作战进程同步、作战效能倍增等方面发挥着至关重要的作用。

利用网络模型分析作战活动过程及信息交互关系，是当前作战建模仿真领域研究的热点和难点问题。国内外相关研究最早可追溯至20世纪60年代，当前主要集中在体系结构分析、作战力量编组、复杂系统建模、作战效能评估等方面。如美军先后提出权力边缘[1]、敏捷性优势[2]等先进作战与指控理念，并依托ELICIT实验平台，围绕作战指控网络开展体系融合、动态控制、深度协作等研究，以成功应对动态和不确定环境的各种挑战；美国Jeff Cares[3]解析了分布式网络化作战的结构特点，建立了信息时代的战斗网络模型；美国Jeffrey和澳大利亚Dekker[4]对作战指控网络进行分析，提出基于复杂网络的指控效能度量方法；白亮等[5]建立了基于控制环的作战网络对抗模型，并给出效能度量指标；滕克难等[6]建立了舰艇编队协同反导作战网络，并对网络化组织作战效果进行度量。

然而，目前的这些研究虽然提升了对作战网络建模问题的认知水平，但多数成果还存在两个方面的不足：一是将作战体系仅看成单一网络，着重考虑了同质节点及其结构特征，未充分关注节点和链路构成的多样性，以及性质、功能、位置等属性的复杂性，对节点与连接关系在整个作战过程中相互影响、相互作用的研究还比较欠缺；二是仅侧重宏观的作战过程分析，对信息流转建模的研究相对较少，对信息流转的网络结构、内在机理、交互关系、运行模式、作用效果等问题分析不够透彻，尚存在较大的研究空间。

作为研究复杂系统与复杂性问题的新方法，超网络理论在作战过程建模、网络结构分析、信息关系描述等方面具有显著的优越性[7]，能较好描述和分析网络多层、节点多级、信息多维的作战信息流转问题，有效弥补了一般复杂网络方法的不足。因此，本文以体系作战条件下的信息流转过程为研究对象，基于超网络理论，提出作战信息流转建模方法，并对所构建超网络模型的拓扑特性进行分析研究，最后以空中突击作战为例，进行仿真验证。

1　作战信息流转超网络特征

1.1超网络

超网络(Super-network)的概念最早在1985年，由美国科学家Sheffi提出，后经Denning、Nagurney等人逐渐丰富完善。超网络通常指规模巨大、连接复杂、节点具有异质性的网络，或网络中嵌套网络，且存在虚拟的节点、边和流等的大型网络，主要特征为网络嵌套网络、多层、多级、多维流量、多种属性/准则等，目前主要应用在互联网、交通、物流、供应链、资金、信息网络等领域，用于描述“高于而又超于现存网络”的网络、分析多层网络结构相互之间的作用与影响、研究网络均衡问题等[8]。

作为一类特殊的复杂网络，超网络更为复杂，但这种复杂性主要表现在属性上，而不是在规模上[9]。通常的复杂网络主要关注节点众多、规模较大的网络，并且为了研究的准确性，节点与边会保持同质，不能完全刻画真实世界网络的特征，尤其是在研究网络中嵌套网络的超大规模网络系统时，难以理清各个网络之间的关系[10-11]。相较而言，超网络主要用来描述和表示不同性质网络之间(特别是层间和级间)的相互作用和影响，并可将不同层次、不同标准的决策者之间的关系用关系函数来表示，同时也更加注重构成要素的复杂交互作用、实体的适应性以及网络的涌现性。

1.2作战信息流转超网络

作战信息流转是指战场信息在不同作战节点之间传播、流通与交互的过程，反映了节点之间多样化的信息交互关系，其网络结构是一个具有典型网络化特征的分层、分布式一体化复杂系统，具有节点异质、链路多重、拓扑时变等特点[12]。根据超网络已有的概念和应用，本文做出如下定义：

定义1作战信息流转超网络(Super-network of operational information flowing，SN_OIF)是指为适应特定作战任务需要，通过多种信息关系将不同类型的作战节点有序连接所构建的不同功能网络(如情报网、指控网及火力网)，经过相互交织而形成的多层次多重边异构网络。

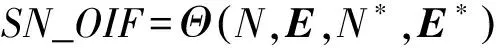
1.3作战信息流转超网络特征分析

对照超网络的基本特征[13]，分析作战信息流转超网络特征，具体为：

1)网络嵌套网络。按功能可分为情报网、指控网、火力网；按传输方式可分为无线网、有线网等。

2)多层特征。可分为物理层、数据链路层、网络层、传输层等。

3)多级特征。信息关系具有多级特征，如指控关系涉及联合指挥所、区域指挥所、师指挥所等。

4)多维流量。信息流包括情报信息、指控信息和火力信息；信息有文本、视频、音频等格式。

5)多种属性/准则。传输方式分无线、有线、光通信等，且需综合考虑信息的完整性、时效性等。

6)拥塞性。由于带宽限制及信息需求的增加，网络中存在着信息拥塞等问题。

7)可能的优化不一致问题。如果每个节点只考虑自身的信息需求，很可能会由于带宽或其他原因造成网络拥塞。

2　作战信息流转超网络模型构建

SN_OIF的基本元素为多种类型的作战节点和信息关系，不同节点按照一定的关联映射规则，通过情报、指控、火力等信息关系进行连接，共同构成超网络模型。

2.1作战节点抽象

根据功能特点，作战节点可分为情报节点、指控节点和火力节点3类。设节点总数为N，情报节点数为n1，指控节点数为n2，火力节点数为n3，则有N=n1+n2+n3。假设第i个节点可用如式(1)的四元组表示。

(1)

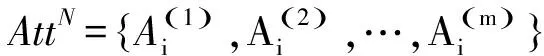
定义2情报节点是指侦察卫星、雷达、预警机等具有预警、探测、侦察、监视能力的作战单元[14]。其集合记为NI，则第i个情报节点可表示为

(2)

定义3指控节点是指各级指挥所、指通机等具有分析决策、资源配置、指令发布等功能的作战单元。其集合记为NC，则第i个指控节点可表示为

(3)

定义4火力节点是指飞机、导弹等具有拦截、攻击、毁伤等能力的作战单元。其集合记为NF，则第i个火力节点可表示为

(4)

综上，SN_OIF的节点集N可表示为N=NI∪NC∪NF，且满足NI∩NC=φ，NC∩NF=φ，NI∩NF=φ。

2.2信息关系抽象

信息关系是指作战节点通过光缆、通信设备等物理连接，实现不同类别信息的交互处理，反映了节点间的信息关联情况[15]。按照功能侧重的不同，可分为情报信息关系、指控信息关系和火力信息关系3类。假设第i个k类信息关系可表示为

(5)

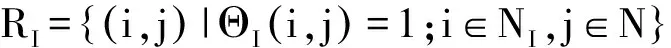
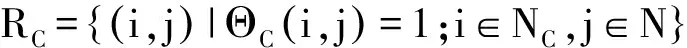
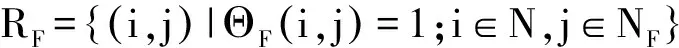
综上，SN_OIF的信息关系集R可表示为R=RI∪RC∪RF，且均为有向边。

2.3关联映射规则

关联映射规则是作战节点与信息关系连接形成功能子网，以及功能子网集成为超网络所遵循的基本准则，主要包括网内关联映射和网间关联映射两类。

定义8基底网是指超网络中的一个特殊子网，可作为其他子网的参照网络。

对于给定的超网络，均存在一个基底网和一个非基底网，将非基底网去除后，剩余的基底网是一个新的超网络；将任何一个子网加入基底网，将形成一个新的超网络，原有的超网络即成为新的基底网[16]。

(6)

(7)

2.4作战信息流转超网络模型

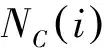
3　作战信息流转超网络拓扑特性的关键指标

超网络多层、多级、多维流量等特征，决定了其具有一般复杂网络所不具备的拓扑特性[19]。文中主要选取节点的超度分布、超边的度分布、介数、聚类系数、子图向心性和网络弹性等6个指标进行分析。

3.1节点的超度分布

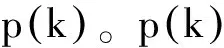
p(k)∞k-τ

(8)

其中，τ为尺度因子。

3.2超边的度分布

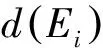
3.3介数

节点i的介数定义为超网络中节点对最短路径中经过该节点个数占所有最短路径数的比例[21]，反映了节点对信息流动的影响力，其一般表达式为

(9)

3.4聚类系数

聚类系数是指节点所有相邻节点之间连边的数目占可能的最大连边数目的比例，主要用来描述网络中节点的集聚情况[22]，即网络有多紧密。对超网络而言，聚类系数的表达式为

(10)

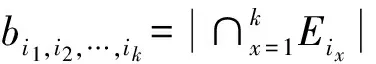
(11)

(12)

同时，伪步长为2的超路数p=3ξ，可得

(13)

3.5子图向心性

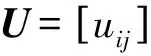
(14)

若i=j，有

(15)

则步长为k的闭链总数CLk为

(16)

由此，可得节点i的子图向心性为

(17)

3.6网络弹性

Martin Christopher和Christine Rutherford将弹性定义为“一个系统在中断或故障后回到原始(或新的更理想)状态的能力”[25]。本文将该定义延伸到超网络，在SN_OIF中，网络弹性主要体现在节点或信息关系遭受敌方攻击、破坏后，拓扑结构仍然能够保持连通的能力，这主要源于节点之间替代途径的冗余性。

定义9网络弹性是指网络发生故障后，回到原始或新的理想状态的能力，可表示为

(18)

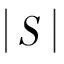
4　仿真分析

以体系作战背景下的空中突击作战为例，运用文中提出的方法，进行基于超网络的作战信息流转建模和特性分析。

4.1空中突击作战过程

假设某作战地域分布有如下作战力量：联合指挥所(UCP，1个)、前进指挥所(FCP，1个)、指通机(CCP，1架)、情报中心(IC，3个)、无人侦察机(UAV，2架)、侦察卫星(RS，4个)、预警机(WP，1架)、电子干扰机(ECP，2架)和歼击机编队(FPF，5个编队共20架)。空中突击作战的高层作战概念如图4所示。

空中突击作战的基本过程为：

第1步UCP受领作战任务后，向IC、RS、UAV下达反映其情报需求的指挥信息。

第2步IC汇总整理已有情报信息并上报，RS飞临作战区域上空收集敌方重要机场、兵力机动等实时情报并回传，UAV深入敌方腹地收集敌地防力量部署、指控系统参数等情报并回传。

第3步UCP汇总分析多源情报信息，定下作战决心，制定作战计划、保障要求等，并作为指挥信息下达给FCP和CCP。

第4步FCP将作战方案细化为适合各作战单元行动的实施计划、兵力部署、协同规定等；CCP根据战场情况，优化调整计划方案，并向RS、UAV、WP下达情报侦察指令。

第5步RS、UAV、WP侦察敌空中兵力出动、地面布防调整等情况，并将情报信息回传至UCP、FCP、CCP和IC。

第6步CCP指挥ECP和FPF灵活机动，突破敌空中、地面阻击力量，对敌重要机场、防空武器阵地等预定目标实施火力打击，并将机动、交战情况及时回传；UCP综合国内外形势变化情况，做出突击停止或继续攻击的指令，并下达给FCP和CCP。

第7步FCP根据指令，及时调整、制定作战方案，组织各类情报、后勤保障；CCP根据指令，指导空中兵力做进一步机动或作战。

上述空中突击作战行动中，信息流转的基本过程如图5所示。其中，虚线框表示作战单元的编队(组网)情况，信息关系与虚线框相连有2种方式，一种是直接连接在火力单元虚线框内的某个节点上，表示仅与该节点进行信息交互，此节点通常为火力单元中指挥权限最高者，如歼击机编队中的长机1、5；另外一种是直接连接在情报单元虚线框上，表示与该框内所有节点都进行信息交互，便于所有情报节点的信息实现全局共享，如情报中心1-3。

4.2SN_OIF模型构建

4.2.1作战节点抽象

空中突击作战中节点包括情报节点、指控节点和火力节点3类共35个，节点属性选取探测(Dc)、指控(C2)、火力(Fr)、机动速度(Mo，单位：km/s)、作战半径(Ra，单位：103km)、高度(Hi，单位：km)、信息质量(Iq)和抗毁性(Su)等8个，具体如表1所示。

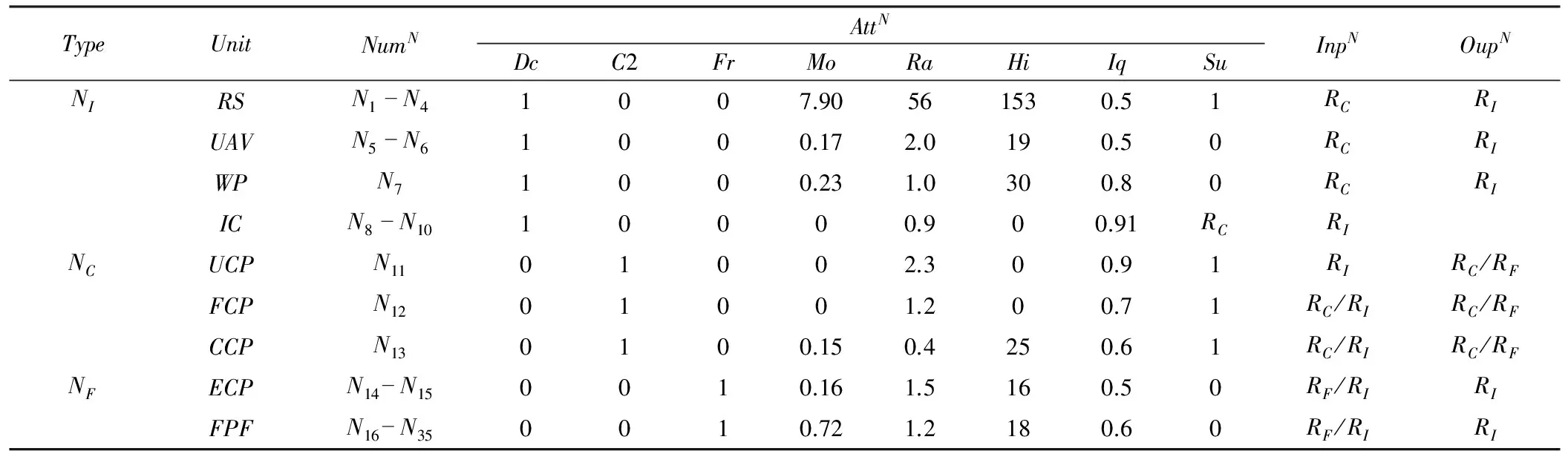
表1　作战节点抽象情况

4.2.2信息关系抽象

空中突击作战中信息关系包括情报信息关系、指控信息关系和火力信息关系3类共200个，其属性主要选取探测(Dc)、指控(C2)、火力(Fr)、时延(Dl，单位：ms)、带宽(Bd，单位：Mbps)和机密性(Se)等6个，具体如表4所示。

表2　信息关系抽象情况

4.2.3SN_OIF模型

将抽象处理后的作战节点和信息关系，按照关联映射规则逐次进行连接组合，建立SN_OIF模型。该超网络模型由结构层和属性层组成，其中，结构层由情报网(GI)、指控网(GC)和火力网(GF)3个子网组成，涉及35个作战节点和200个信息关系，属性层由节点属性和信息关系属性组成，共11个，具体如图6所示。

4.3SN_OIF特性分析

根据所构建的空中突击作战SN_OIF模型，结合各拓扑特性关键指标的概念内涵及计算公式，进行如下分析：

4.3.1节点的超度分布

结合SN_OIF节点的邻接矩阵，经过分析计算，可得节点超度分布的CCDF(Complementary Cumulative Distribution Function)图，如图7所示。曲线斜率逐渐由小增大，在k=11处，斜率迅速增加，在整体上服从指数截断的幂律分布，这说明SN_OIF各节点之间的连接状况(超度数)具有明显的不均匀分布性，总体呈现无标度特性，即由大部分超度值相对较低的节点和少数超度值较高的节点组成。通过进一步分析发现，超度值较高的节点为指通机、联合指挥所、侦察卫星和预警机，这是因为这些节点是指控网和情报网的核心，各类情报信息流、指控信息流和火力信息流在此交汇流通，信息交互频繁，信息关系复杂交织。

4.3.2超边的度分布

结合SN_OIF超边的邻接矩阵，经过分析计算，可得SN_OIF中信息关系的度分布CCDF图，如图8所示。超边的度分布曲线斜率也是逐渐由小增大，在kE=105处，斜率迅速增加，在整体上服从指数截断的幂律分布，具有较为明显无标度特性，即大部分信息关系的度值相对较低，只有少量信息关系的度值较高。通过进一步分析发现，度值较高的超边所连接的节点均为侦察卫星、指通机、联合指挥所、预警机、前进指挥所、情报中心等作战信息流转的关键节点，信息交互种类、传输量的需求均显著高于其他信息关系。

4.3.3介数

根据公式(8)，计算得出SN_OIF的节点介数平均值为23.89，节点介数与节点超度值之间的相关性分布如图9所示，二者之间的相关系数为0.63，表明超度值较低的节点具有较小的介数(例如歼击机2的超度值为2，介数为0)，超度值较高的节点具有较高的介数(例如预警机的超度值为22，介数为40.26)。而图14中也显示出虽然有些节点的超度值较小，但仍具有很大的介数(例如电子干扰机1的超度值为10，介数为33.83)，这些度值较小的节点通常在作战编队中担负指挥引导、信息发布等功能，与其他节点有着密切的信息交互关系，在诸多节点的相互沟通中起到关键的桥梁作用。

4.3.4聚类系数

根据公式(9)，计算SN_OIF的节点聚类系数和平均聚类系数，如表3所示。该超网络的平均聚类系数为0.52，相对于随机图或随机幂律图具有较高的聚集性，表明节点之间的连接关系较为紧密，这是因为空中突击作战攻防对抗激烈、作战节奏快，信息流围绕各类指挥平台和打击力量纵横交织流转，使得作战体系内部连接十分紧密。

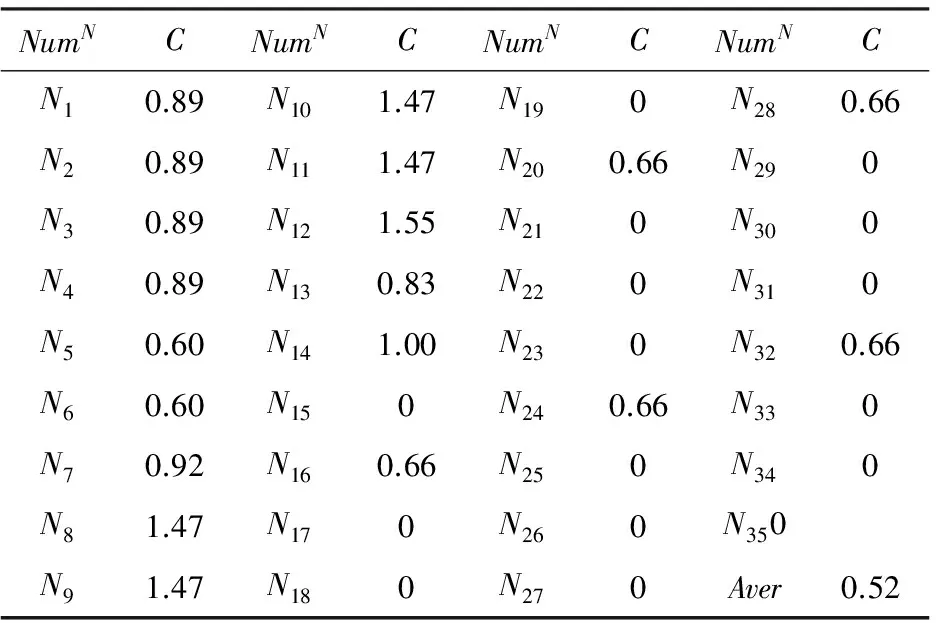
表3　SN_OIF聚类系数

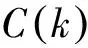
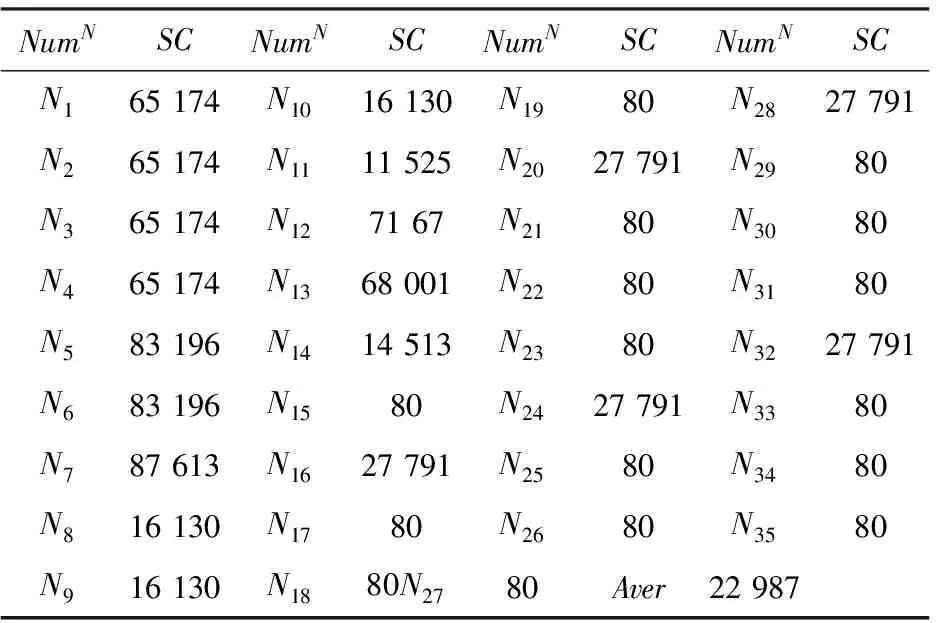
表4　SN_OIF子图向心性

4.3.5子图向心性

根据式(13)-(16)，计算SN_OIF的节点子图向心性和平均子图向心性，如表4所示。可见，子图向心性最高的节点是预警机，反映了其在空中作战体系中的核心地位，是大量情报、指控信息关系的交汇点和信息流转的关键点，对空中突击作战网络化效能的贡献度最高。同时，子图向心性最低的节点是歼击机编队和电子干扰机编队，说明其作为空中作战的末端执行节点，与其他类型节点交互信息的种类和数量相对较少，仅有部分信息流转至该节点。

图11给出了节点子图向心性随步长的变化曲线。可以看出，整体而言，子图向心性随着步长的增加而上升，达到峰值后(侦察卫星、无人机步长为9时，其他节点步长为8时)又逐渐下降。上升的原因是步长增加后，节点之间复杂交织的连接关系提高了路径选择的可能性；下降的原因是子图向心性达到峰值后，主要节点均已参与到闭链中，降低了节点可选择和变化的可能性。需要指出的是，火力节点的子图向心性均低于情报节点和指控节点，这是因为火力节点位于作战指挥链的末端，仅执行交战打击任务，不参与作战筹划、指挥决策、力量调配等信息交互密集的前期阶段，没有形成较多的信息环路，因而子图向心性总体偏小。

4.3.6网络弹性

受论文篇幅所限，此处仅考虑因单个节点遭敌彻底毁伤且不可修复的情况，分随机攻击和蓄意攻击两种情况进行研究，其中蓄意攻击策略又分为度值优先去点攻击、介数优先去点攻击和聚类系数优先去点攻击3类。根据式(17)，假设每个时刻有1个节点遭敌毁伤破坏，得出超网络的弹性值变化情况如图12所示。从图中可以看出，随着攻击时刻的不断增加，网络弹性值总体呈现下降趋势，但局部存在递增现象，即变化曲线不是严格的单调递减。主要原因是随着受毁伤节点数的增加，网络中孤立节点的比例在局部可能存在增加的现象，而对孤立节点的删除将使网络的自然连通度增加，即增强网络弹性。

对于随机攻击，网络呈现出较强的鲁棒性，网络弹性值下降最慢，在时刻33趋于0。相较而言，蓄意攻击使网络弹性值下降较快，其中按介数去点对网络弹性值的影响最快，在时刻17趋于0；其次是按度值去点，在时刻19趋于0；最后是按聚类系数去点，在时刻20趋于0。这是因为介数直接反映了网络中的关键节点，而聚类系数和度值仅是从不同侧面对节点重要程度的度量。因此，按介数去点能直接删除对网络功能结构影响最大的节点，快速降低网络的弹性值。

5　结语

作战信息流转建模是研究战斗力生成过程，破解信息制胜机理的关键[26]。本文基于超网络理论，通过分析作战信息流转的超网络特征，抽象作战节点和信息关系，定义关联映射规则，提出“两层三网”的作战信息流转超网络建模方法，并选取节点的超度分布、子图向心性、网络弹性等6个测度进行拓扑特性分析，为作战信息流转运行机理量化建模提供了有益参考。由于超网络拓扑结构对于作战信息流转的路径规划、作战效能、风险管控等具有重要影响[27]，下一步将综合考虑网络信息流量、传输时延和信息质量，对所构建的超网络模型进行优化重构。

[1]Alberts D S, Hayes R E. Power to the Edge[M]. Washington, DC: CCRP Publication Series, 2003:17-37.

[2]Alberts D S. The Agility Advantage: A Survival Guide for Complex Enterprises and Endeavors[M]. Washington, DC: CCRP Publication Series, 2011: 4-10.

[3]杰夫·凯尔斯. 分布式网络化作战—网络中心战基础 [M]. 北京：北京邮电大学出版社, 2006.

[4]Jeffrey R C. An information age combat model [C]// International Command and Control Research and Technology Symposium (ICCRTS). Washington D C, 2004: 28-65.

[5]白亮, 肖延东，侯绿林，等. 基于控制环的作战网络对抗模型[J]. 国防科技大学学报, 2013, 35(3): 42-47.

Bai Liang, Xiao Yandong, HouLülin,et al. Operational network combat model based on control loop[J]. Journal of National University of Defense Technology, 2013, 35(3): 42-47.

[6]滕克难, 盛安冬. 舰艇编队协同反导作战网络效果度量方法研究[J]. 兵工学报, 2010, 31(9): 1247-1253.

Teng Kenan, Sheng Andong. Research on metric of network effect in ship formation cooperation anti-missile operation[J].Acta Armamentar II, 2010, 31(9): 1247-1253.

[7]Nagurney A, Dong J. Supernetworks: Decision-Making for the Information Age [M]. Cheltenham: Edward Elgar Publishing, 2002.

[8]Nagurney A, Cruz J, Matsypura D. Dynamics of global supply chain super-networks [J]. Mathematical and Computer Modeling, 2003, 37(9/10):963-983.

[9]王志平, 王众托. 超网络理论及其应用[M]. 北京: 科学出版社, 2008.

[10] Watts D J, Strogatz S H. Collective dynamics of small-world networks[J]. Nature, 1998, 393(6684): 440-442.

[11] Barabási A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512.

[12] Shi F L, Lei Y L, Zhu Y F. A military communication super-network structure model for net centric environment [C]∥International Conference on Computational and Information Sciences. Wuhan, 2010.

[13] 邹志刚, 刘付显，孙施曼，等. 基于扩展粒度计算的防空体系结构超网络模型[J]. 复杂系统与复杂性科学, 2014, 11(2): 24-35.

Zou Zhigang, Liu Fuxian, Sun Shiman,et al. Extended granular computing-based on supernetwork model for anti-air operational architecture[J]. Complex Systems and Complexity Science, 2014, 11(2): 24-35.

[14] Anthony H D. Analyzing C2 structures and selfsynchronization with simple computational models[C]∥International Command and Control Research and Technology Symposium. New York, 2011: 64-98.

[15] Akella R, McMillin B M. Information flow analysis of energy management in a smart grid [J]. Lecture Notes in Computer Science, 2011(01):263-276.

[16] 邵峰晶, 孙仁诚，李淑静，等. 多子网复合复杂网络及其运算研究[J]. 复杂系统与复杂性科学, 2012, 9(4): 20-21.

Shao Fengjing, Sun Rencheng, Li Shujing,et al. Research of multi-subnet composited complex network and its operation[J]. Complex Systems and Complexity Science, 2012, 9(4): 20-25.

[17] 胡枫, 赵海兴，何佳倍，等. 基于超图结构的科研合作网络演化模型[J]. 物理学报, 2013, 69(19): 1-8.

Hu Feng, Zhao Haixing, He Jiabei,et al. An evolving model for hypergraph-structure-based scientific collaboration networks[J]. Acta Phys Sin, 2013, 62(19): 198901.

[18] Zou Z G, Liu F X, Sun S M. et al. Ripple-effect analysis for operational architecture of air defense systems with supernetwork modeling [J]. Journal of Systems Engineering and Electronics. 2014, 25(2): 249-263.

[19] 郭进利, 祝昕昀. 超网络中标度律的涌现[J]. 物理学报, 2014, 63(9): 090207.

Guo Jinli, Zhu Xinyun. Emergence of scaling in hypernetworks[J].Acta Phys Sin, 2014, 63(9): 090207.

[20] Liu Q, Fang J Q, LI Y. Analysis of Layer Cross-degree on Super-network Models [R]. Beijing: Annual Report of China Institute of Atomic Energy, 2013.

[21] Albert R, Barabási A L. Statistical mechanics of complex networks[J]. Rev Mod Phys, 2002, 74(1): 47-97.

[22] Wu K, Xi Y J, Liao X. Analysis on current research of supernetwork through knowledge mapping method[C]∥6th International Conference on Knowledge Science, Engineering and Management, Dalian, 2013: 15-22.

[23] Estrada E, Rodrigues V R. Sub-graph centrality in complex networks [J]. Physical Review E, 2005,71(5):1-9.

[24] Enokido T, Takizawa M . Purpose-based information flow control for cyber engineering [J]. IEEE Transations On Industrial Electronics, 2011: 2216-2225.

[25] Xia, Lu, Xing, Qing-Hua, Zou, Zhi-Gang. Supernetwork model of operational system-of-systems for capability emergence[C]. The 31st Chinese Control Conference, Hefei, 2012: 1142-1146.

[26] Agaskar A, He T, Tong L. Distributed detection of multi-hop information flows with fusion capacity constraints [J]. IEEE Transactions On signal Processing, 2010: 3373-3383.

[27] Yao J, Huang J Y, Chen G R. et al. A new coupled-map car-following model based on a transportation supernetwork framework [J]. Chin Phys B, 2013, 22(6): 060208.

(责任编辑耿金花)

Modeling and Characteristic Analyzing of Operational Information Flowing Based on Super-Network

YANG Yinghui1, LI Jianhua1, WANG Gang1，NAN Mingli1,2

(1.Information and Navigation College, Air Force Engineering University, Xi’an 710077, China；2.The Unit 95881 of PLA,Beijing 100095,China)

Aiming at the problem that information network with single factor pattern can not reflect effectively the complex structure and dynamic process for operational information flowing (OIF), this paper presents a new method of modeling and characteristic analyzing for OIF model with double layers and three networks based on super-network. Firstly, super-network structure characteristics of OIF are analyzed, multidimensional attributes for operational nodes and information relationships are abstracted, association mapping rules are defined, and then OIF super-network model is built. Secondly, from the perspective of super-degree distribution for nodes, degree distribution for super-edges, betweenness, convergence coefficient, sub-graph centrality and network resilience, topological characteristics of OIF super-network are studied. Finally, taking aviation aggressive operation as an example,and simulation results validate feasibility and rationality of the model and method.

operation; information flowing; super-network; association mapping; topological characteristic; sub-graph centrality; network resilience

1672-3813(2016)03-0008-11;DOI:10.13306/j.1672-3813.2016.03.002

2014-12-02；

2015-01-23

国家自然科学基金(61401499,61174162)；国家社会科学基金(14GJ003-172,12GJ003-130)

杨迎辉(1988-),男,河南洛阳人,博士研究生,主要研究方向为作战信息流转、复杂系统建模。

E82

A