基于IMF能量熵的脑电情感特征提取研究*

陆苗，邹俊忠，张见，肖姝源，卫作臣

(华东理工大学，上海 200237)

1 引 言

情感识别的关键是从脑电信号中提取有效的情感特征，提高分类准确率。脑电信号是一种非平稳非线性随机信号，分析这类信号的基本方法有时域、频域和时频分析，由于信号的时域和频域之间相互关联，因此，时频分析方法会更准确。经验模态(EMD)分解是一种自适应信号时频分析方法，在处理脑电信号这一类非平稳非线性随机信号上具有明显的优势。

目前，EMD算法在国内外脑电信号处理研究中的应用非常广泛。季忠利将EMD算法应用到脑电信号病理研究中，得到脑信号各个频带的强度值，准确判定了脑电信号节律特征[1]。沈学丽将HHT和小波包变换结合起来，应用到睡眠脑电信号分期研究中[2]，细化了睡眠分期的过程。李淑芳等人从癫痫脑电中提取IMF分量的能量值、幅值和波动指作为特征[3]，提高了癫痫脑电的识别正确率。李阳等人用希尔伯特-黄变换提取了不同节律的能量作为特征，在运动想象脑电信号的识别中取得了良好的效果[4]。Ranjit等学者将EMD分解应用到眼电信号的变化研究中，计算眼电信号的各个IMF分量的希尔伯特加权频率，作为脊柱损伤者眼电信号的特征，并同健康者的眼电变化进行了对比研究[5]。

另外，分析国内外学者的研究成果发现，EMD方法在运动想象脑电、病理脑电信号以及眼电信号的特征提取研究中应用的比较多，但是在情感脑电中的应用还显得不足，因此，将EMD用于情感识别的研究很有必要。

2 脑电信号采集

研究对象为年龄在23到25岁的华东理工大学研究生，要求每个被试者均身心健康、无心脏病、脑损伤和精神类疾病病史，被试者可自愿选择是否参与试验。

采集信号之前需要注意：准备环境安静的实验场所，防止脑电信号中混入过多外界干扰；被试者要保证良好的精神状态，不能剧烈运动或饮用含有咖啡因的饮料；提前告知被试者实验方法和目的；实验前要将头皮洗净，避免过多的头皮阻抗给采集带来干扰。首先让被试者处于安静闭眼的状态下采集一组信号，作为对照组，然后通过音乐播放器对20个音乐片段进行播放，前10个片段诱发被试者的愉悦情绪，后10个片段诱发被试者的悲伤情绪，每段音乐播放完毕后，有120 s的过渡时间使之平静，并让被试者填写情感状态自我评估表，120 s后播放器自动播放下一段音乐。信号的采样频率为128 Hz，数据长度为50 min，将采集的脑电信号数据存储为matlab能够识别的格式。

3 脑电信号特征提取

3.1 EMD分解原理

EMD分解的基础是采集到的数据自身的局部特性，具有很强的自适应性。

对信号进行EMD分解后将获得若干个频率范围不同的由高频到低频排列的IMF函数序列，这些IMF函数必须满足下面两个条件：

a. 在采样信号的整个过程内，信号的局部极值点的数目和过零点数目相等或最多相差1；

b. 任意时刻，由局部极大值构成的上包络线和由局部极小值构成的下包络线关于时间轴局部对称。

EMD分解的过程描述如下：

(1) 找到原始信号x(t)的全部局部最大值和局部最小值，用插值算法获得上下包络线，然后求得上下包络线的均值m，定义h=x(t)-m。

(2) 判定h(t) 是否满足IMF分解终止条件，若不满足，则令x(t)=h，执行第一步；若满足，执行下一步。

(3) 令ci(t)=h，表示分解得到的第i个IMF分量，并令ri(t)=ri-ci。

(4) 判断是否满足IMF分解终止条件，如果满足就进行下一步；如不满足，则令x(t)=ri，回到第一步，i=i+1 。

(5) 分解终止，最终原始信号被分解成n个固有模态分量c1，c2，…，cn和一个残差rn，即：

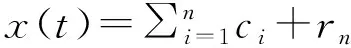
(1)

3.2 EMD分解的缺陷与改进

由EMD分解原理和步骤可知，上下包络线是通过对信号的局部极大值和局部极小值进行三次样条插值拟合曲线得到的，然后根据上下包络线求平均。那么在端点处就会出现一个问题，我们不能保证数据在端点处恰好是极大值点或极小值点，那么在进行三次样条插值的时候很有可能产生拟合误差，这种缺陷叫做“端点效应”。以周期谐波函数X为例，假设：

X=sin(2πt)+cos(4πt)+0.8cos(10πt)

(2)

X为三个正余弦函数叠加而成，频率分别为1、2和5 Hz，周期为1 s。图1为此信号EMD分解求取的上下包络线和均值，从图中可以看出信号在左端点处并没有被确定为极值点，因此，当用三次样条插值进行数据拟合时，信号的上包络线和实际的曲线产生了明显的误差，由于每一次的迭代会用到上一步获得的均值，那么每次均值的误差被积累到下一次，这样的逐次误差积累给信号的分解会造成极大影响，严重的可能使信号分解失去意义。

因此，需要消除这一缺陷或者减少端点效应对信号分解的影响。在传统的EMD分解算法中，通常使用三次样条插值算法对信号的极大值点和极小值点进行拟合，但是在端点处，三次样条插值算法的平滑性不足，会造成过冲现象，那么可以考虑使用平滑度更高的幂函数插值，使用分段幂函数插值算法能够对端点处进行平滑处理，从而抑制端点效应的影响。图2为传统EMD方法的分解结果，图3为改进的EMD方法的分解结果，对比图2和图3可以看出，改进后的EMD方法的分解结果更加精细。

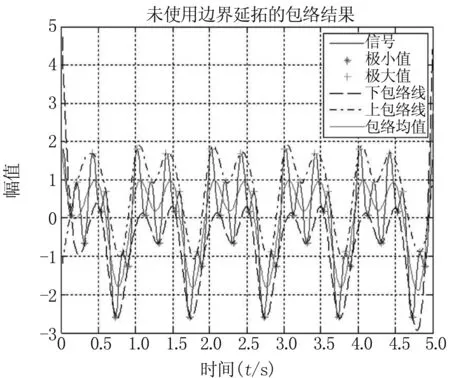
图1 端点效应实例图

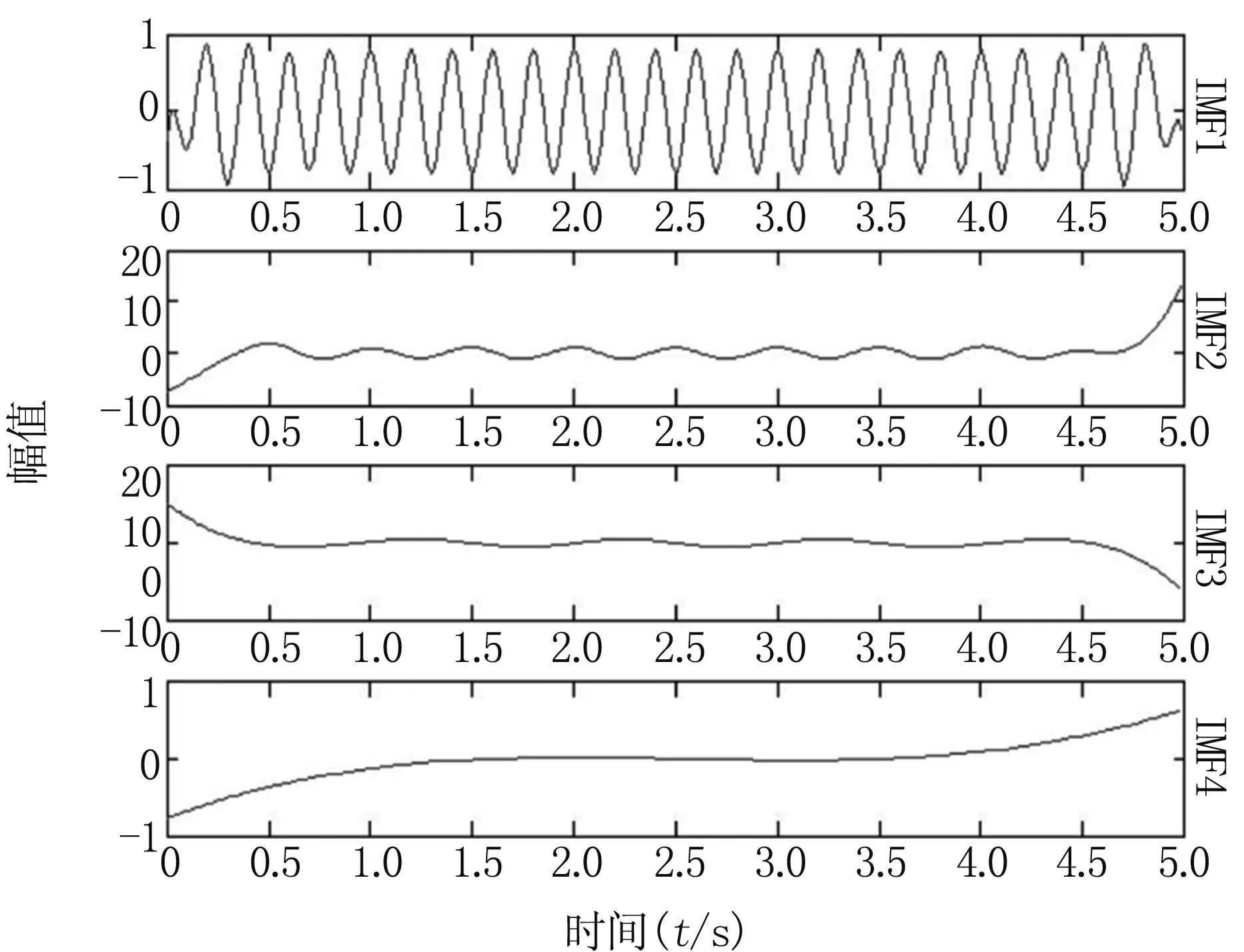
图2 传统EMD分解效果

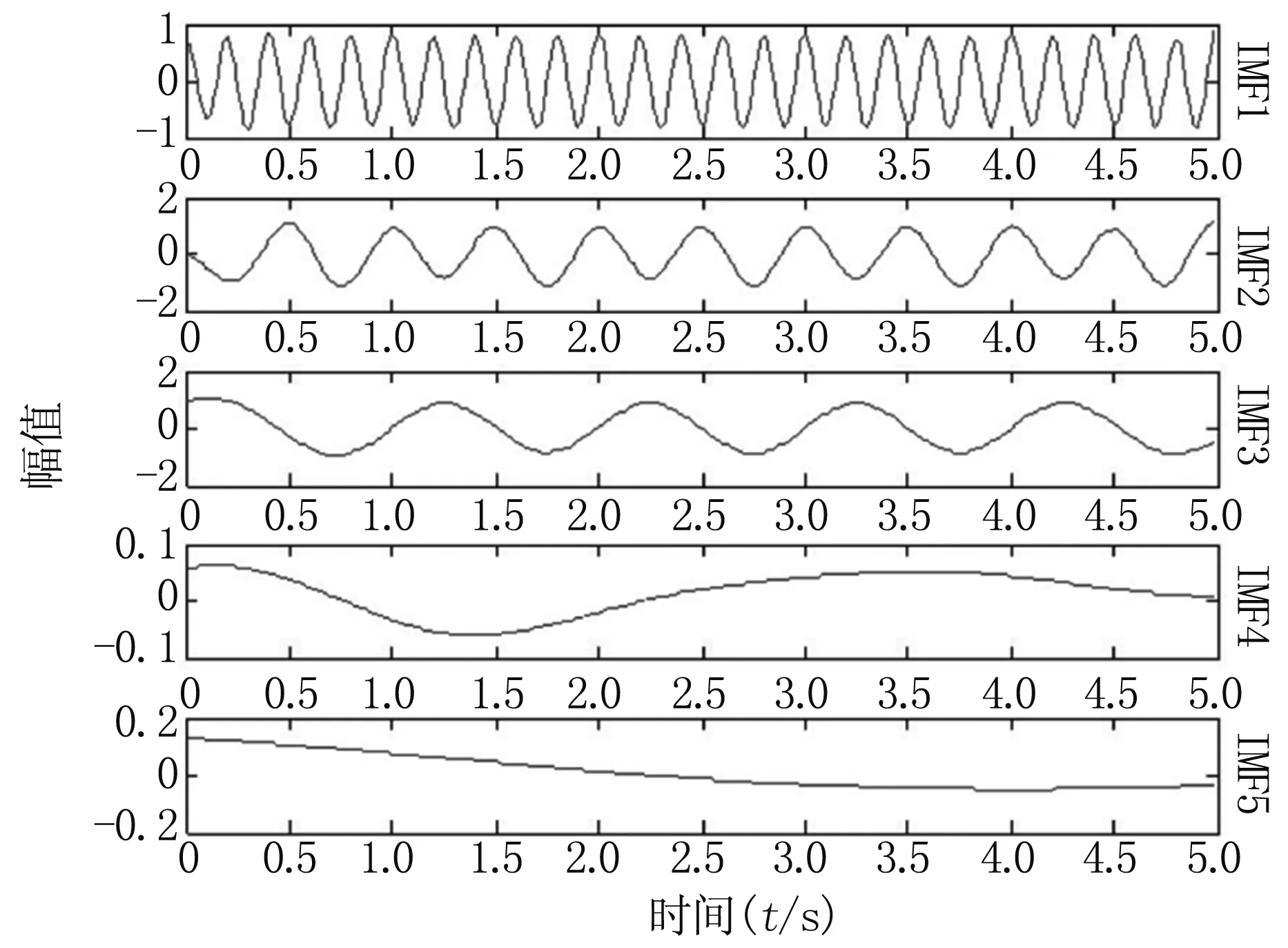
图3 改进EMD分解效果

为验证改进后的EMD算法具有更高的精度，这里引入相关系数来描述实际分解结果与理想分解结果的相似程度，定义信号x(n)和y(n)的相关系数为：

(3)

当x(n)=y(n)，即两个信号完全相等时，ρxy=l；当x(n)和y(n)完全不相关时，ρxy=0；当x(n)和y(n)之间有某种关系时，|ρxy|的数值在0和1之间表示两者的相关程度。表1为原始的EMD算法和改进算法求得的IMF分量与理想IMF分量的相关系数。

从表1中可以看出，对传统EMD算法改进之后，相关系数的数值得到明显的提高，说明通过改进的EMD算法的分解结果更加精确。

表1 原始算法与改进算法的相关系数

3.3 脑电信号EMD分解

根据EMD分解流程，对实验采集到的三类情感脑电信号进行n阶分解，获得n个IMF分量和残余项。这里对脑电信号样本数据进行8阶EMD分解，图4所示从左到右分别为平静、悲伤、愉悦三种情感状态脑电信号的前4阶IMF分量。

从图4中可以看出，不同类别的脑电信号含有的频率成分不同，且所含频率的高低和阶数成正比，从幅度上看，同阶的IMF分量的幅度的差异很大，平静时第三阶IMF分量幅值较大，悲伤时第二阶和第三阶IMF分量的幅值较大，愉悦时各个分量幅值基本相同，可以考虑将IMF能量或与IMF能量相关的量作为脑电信号的情感特征。

图4 三种情感脑电信号EMD分解

3.4 脑电信号IMF能量熵

“熵”的概念最早出现在热力学研究中，也叫做“热熵”，用来表示一个系统中分子状态的均匀状况，分子状态越均匀，熵值越高，当系统中分子分布最均匀时，熵值达到最大。“信息熵”是香农于1948年提出的一个抽象概念，用来描述信源的不确定度，这些概念成功解决了对信息的量化度量的问题。信息熵表征的是某一信息出现的概率，它与热熵互为负量，当信息广为传播时，说明信息出现的概率高，反映的是信息的价值。

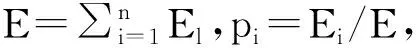
(4)

4 脑电信号情感识别实验

脑电信号处理过程为：首先对原始脑电信号进行预处理，去除眼电心电等伪迹，然后对信号进行经验模态分解，得到IMF分量，根据能量熵的概念计算 IMF能量熵，从中选取特征向量，通过分类器对三种情感状态的信号样本进行分类实验，最后得到分类结果。

对平静、悲伤、愉悦三类情感信号进行分类实验，从每一类信号中选出数据长度为500的共120个样本，再随机选出30个作为标准样本，最后从剩下的样本中选出45个测试样本。

实验中，分别使用传统EMD算法和改进EMD算法对样本数据进行8阶EMD分解，结合能量熵获得脑电信号的情感特征，表2为利用传统EMD算法进行实验的平均分类准确率，表3为利用改进EMD算法进行实验的平均分类准确率。

分析表2和表3的结果，发现改进EMD算法后，不管是对标准样本还是测试样本，平局分类准确率提高了15%左右，结果表明改进的EMD算法应用到特征提取中能有效地提高分类准确率。

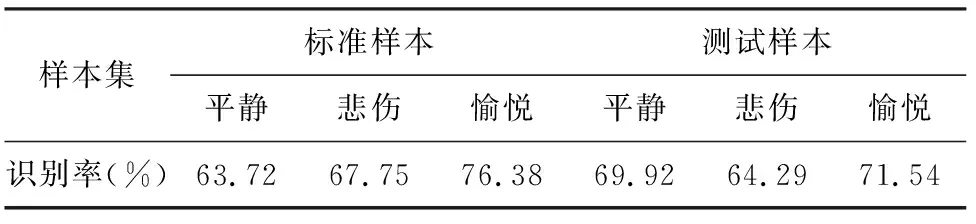
表2 传统EMD算法平均分类准确率

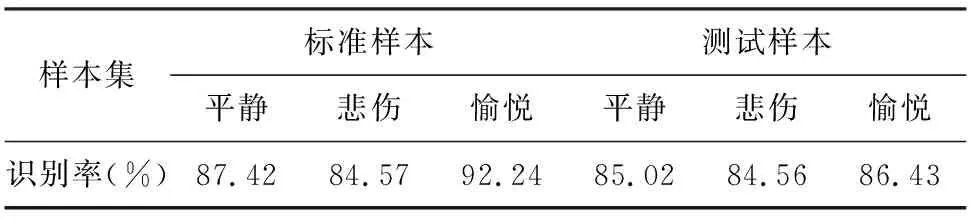
表3 改进EMD算法平均分类准确率

表4所示为样本分类结果。

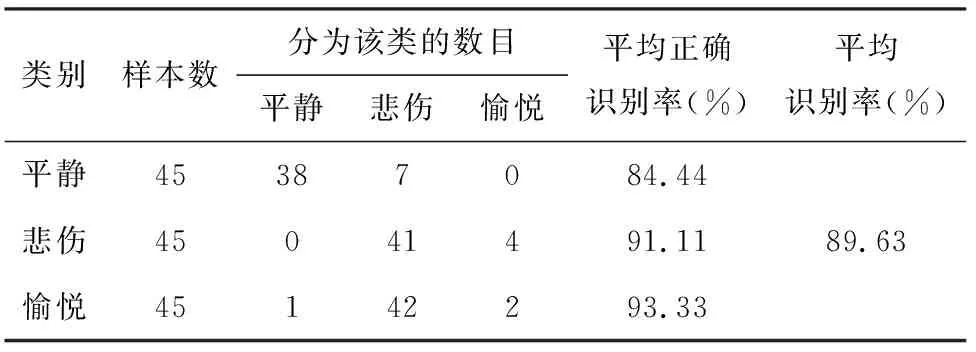
表4 基于IMF能量熵得到的分类结果

从表中可以看出，基于IMF能量熵的情感识别中，对愉悦情感的识别效果最好，对平静的识别效果稍显不足，总体平均识别率达到80%以上，说明IMF能量熵用于脑电信号情感识别是有效的。

5 总结与展望

本研究对脑电信号情感识别的特征提取进行了研究，针对传统EMD分解中存在的端点效应，选择了分段幂函数插值代替三次样条插值，提升了EMD算法的分解精度，将其应用到脑电信号特征提取中取得了较好的效果。

除了IMF能量熵，从信号的IMF分量中还可以提取IMF能量矩、IMF近似熵、IMF幅值等作为特征，结合改进的EMD分解能否取得更好的识别效果仍有待研究。