基于逆运动学的下肢步态参数计算和测量*

王勇哲，沈林勇，章亚男，钱晋武

(上海大学机电工程与自动化学院，上海 200072)

1 引 言

临床应用中，步态分析是研究步行规律的检查方法，旨在通过生物力学和运动学手段，揭示步态异常的关键环节及影响因素，从而指导康复评估和治疗，也有助于临床诊断、疗效评估及机理研究等[1]。不仅在康复评估方面，“关键转变的早期预警”是当今国际研究的热点，不同领域相关研究在《Nature》等国际科技刊物上多有发表[2-5]。这些研究表明，系统突变的早期预警信号是普遍存在的，不因系统的细节差异而异，神经疾病也存在早期信号，因此，应用步态分析研究早期预警信号是一种新的尝试且具有一定的理论支持。

现阶段的步态参数获取方法很多，如基于特征融合的步态识别中利用图像处理与关节点定位的方法获取关节角度，该方法测量方便但计算复杂，由于关节点是根据比例来确定的，所以精度也会有所影响[6-7]。基于Kinect骨骼跟踪功能的骨骼识别系统研究中，用Kinect和图形处理的步态测量方法，由于Kinect主要应用在游戏方面，在人移动或者与Kinect距离变化均会导致人体下肢杆长变化和关节角度变化，数据精度能否用在神经疾病的康复与评估中还需要进行探究[8]。使用光学标记点来测量步态参数的方法也存在标记点滑移和遮挡等问题[9]。为了能够精确、方便的测量步态参数，本研究提出基于机器人逆运动学的步态参数计算方法，解决了机器人逆运动学算法在人体上的应用问题，平衡了实验方便性与精度。

2 下肢建模

2.1 下肢关节角度定义

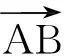
图1 人体下肢关节角度定义

2.2 逆运动学建模

本研究将人体下肢的大腿、小腿和足三部分分别简化为三个刚体，各刚体之间均设为转动关节联接且在矢状面中进行建模分析。康复医学中描述的踝关节转角的定义并不是脚与小腿之间的夹角，而是脚底直线与小腿之间的角度θAnkle，这与3连杆机器人结构有些区别。因此分析图1中角度几何关系，作过C点且平行于ED的直线CF，BC与CF即为踝关节夹角。由此可以得到人体下肢逆运动学计算模型，坐标系建立见图2。

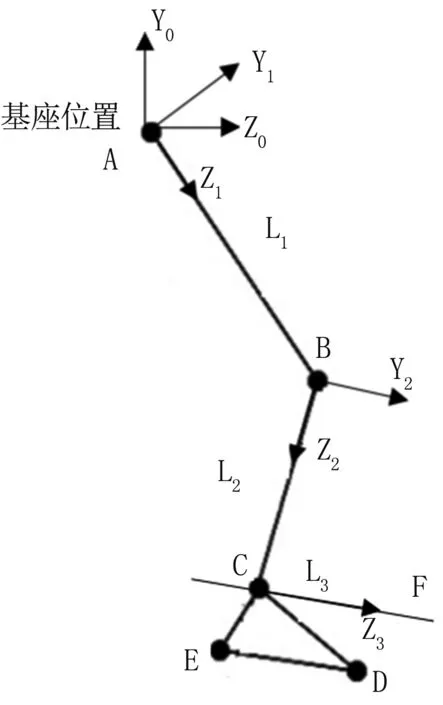
图2 逆运动学建模坐标系

根据D-H参数建模法[12]可以得到机器人坐标变换矩阵T关系如下：

(1)

其中s代表sin函数，c代表cos函数，且S123=Sin(θ1+θ2+θ3)；由逆运动学几何解法可推导出3个关节角度的计算公式，首先可以计算出膝关节角度：

(2)

膝关节角度公式有两个解，选取符合人体下肢运动关系的角度进行计算(这里取正解)。髋关节角度计算公式：

θhip=±arctan(s1，c1)

(3)

其中s1和c1分别满足公式(4)和公式(5)。

(4)

(5)

踝关节角度计算公式：

θAnkle=arctan(s123，c123)-θhip-θknee

(6)

3 实验方案与计算原理

3.1 实验方案设计

利用光学运动捕捉系统配套的Marker点做了符合实验原理的脚刚体固定装置，原理见图3。装置一共用6个标识点组成一个刚体，其中3个标识点在A面3个在B面，A与B面形成一定的角度能够保证位置传感器至少识别到3个标识点，从而解决遮挡丢点的问题。该装置还增加了一个标杆，来设定每次试验时标定图2中C点的位置就在标杆的上端点，这样对同一个人试验能够保证C点位置不变。

图3 脚上刚体固定装置原理图

光学运动捕捉系统中脚刚体的局部坐标系的姿态见图3。坐标系中Y轴垂直脚底面向上，Z轴平行于脚底面沿着脚尖方向。人体下肢标识点的设定方法有很多，如Helen Hayes标识点设定方法、3点组标识点设定和群点法设定等，本实验标识点的设定参考Helen Hayes标识点设定方法。见图4，根据实验的设计需要在大腿旋转中心(根据计算的位置标定)、股骨外髁、外踝、脚跟和第二跖骨处设定标识点[13-15]，由上述标识点使用向量法就可以算出下肢关节角度，但根据提出的逆运动学方法只需要大腿旋转中心和外踝位置点。

3.2 下肢杆长计算原理

要计算出关节角度θHip、θKnee、θAnkle需要得到L1和L2的长度，即大腿长度和膝关节中心到C点距离。由于用尺子测量腿长会有较大的误差，需要通过其他方法来测定。为了解决这个问题，在腿上固定一个标识点，根据标识点的运动轨迹间接的求出关节旋转中心。

图4 Helen Hayes标志点设置方法

图5 测量腿长动作示意图

首先在人体大腿偏下和小腿偏下各固定一个标识点，坐在椅子上依次进行抬大腿动作、大腿不动抬小腿动作，见图5。这两个动作算一次测量，在一次测量中需要人坐在椅子的同一个位置，期间不能使臀部产生位移。通过一次测量，可以得到2个标识点的空间轨迹，我们使用最小二乘拟合圆弧的方法拟合圆弧并求出圆弧中心，即髋关节旋转中心和膝关节中心。

由圆的方程(7)两式可知，求出参数a,b,c即可得到圆半径和圆心参数。

R2=(x-A)2+(y-B)2
x2+y2+ax+by+c=0

(7)

其中x,y为变量，点(Xi，Yi)到圆心的距离为di，最小二乘法运算的样本集可以表示为：

d2=(Xi-A)2+(Yi-B)2

(8)

则点(Xi，Yi)到圆边缘的距离的平方与半径平方的差为：

(9)

因此只需求解参数a,b,c使得公式(10)的Q(a,b,c)的值最小即可。

(10)

以上算法根据标识点运动数据可以拟合圆弧得到圆弧中心，大腿旋转中心和小腿旋转中心长度即为大腿长度L1，通过运动捕捉仪识别的点C坐标和小腿旋转中心可以算出L2。

图6 坐标变换原理图

3.3 计算位姿矩阵

实验设备不能够直接得到脚刚体相对于髋关节旋转中心的位姿矩阵，需要进行几次坐标变换。坐标系变换原理见图6，通过光学运动捕捉仪得到设备坐标系下坐标系0、坐标系3的位置与姿态，即可算出T1矩阵和T2矩阵，T1和T2满足公式(11)如下：

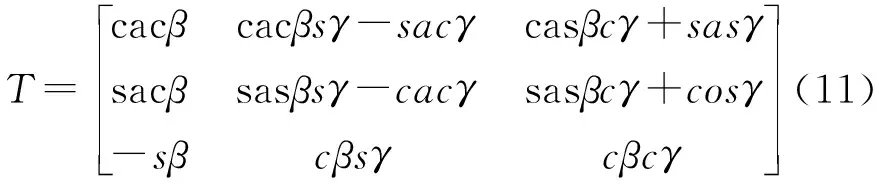
T1为坐标系0相对于设备坐标系的变换矩阵，T2为坐标系3相对于设备坐标系的变换矩阵。因此坐标系3相对于坐标系0的变换矩阵T3为：

(12)

4 实验对比分析

4.1 验证实验方案

为了说明上述方法计算出人体下肢关节角度的精度情况，用医学专用人体骨骼模型进行对比实验分析。首先人体骨骼较细，能够通过光学运动捕捉仪精确的测量其下肢长度，其次，可以得到实际的人体下肢模型关节角度。对比实验方法：通过光学运动捕捉仪获取固定在骨骼上的虚拟点坐标(图4所示)，通过点计算向量夹角得到实际的人体骨骼模型角度(简称向量法)，向量法算出的数据可以作为误差分析的真值处理。

首先需要计算医学骨骼模型的下肢杆长，为了说明下肢杆长计算方法的正确性，同时使用光学运动捕捉仪测量进行比较。实验数据见表1，其误差在3 mm左右，由于测量人体下肢长度范围一般在400～500 mm之间，误差大小只占有0.75%左右，影响较小。

表1 人体下肢杆长数据

实验中，手驱动医学骨骼模型下肢连续运动，连续采集5 s。独立重复上述过程5次，通过逆运动学方法和向量法分别计算运动过程中髋关节、膝关节和踝关节角度的变化序列。以下对两种方法算出的数据进行误差分析和相关性分析。

(1)根据误差数据分析方法[16]，我们认定向量法计算出的数据为接近真值A0的A，逆运动学计算出数据为测量值X。则相对误d为：

d=X-A

(13)

算数平均误差δ平和标准差σ分别为：

(14)

(15)

n为测量次数，di为第i次测量的误差。

测量各个关节角度的算数平均误差δ平和标准误差σ见表2。此结果是每次实验所有数据的算术平均误差和标准误差，但是人体下肢髋关节、膝关节和踝关节的转角范围不同，所以同样的误差对于不同关节的影响大小是不一样的，一般人体下肢髋关节转角范围是-15°～ 35°、膝关节转角范围0°～ 65°和踝关节转角范围-10°～ 25°。

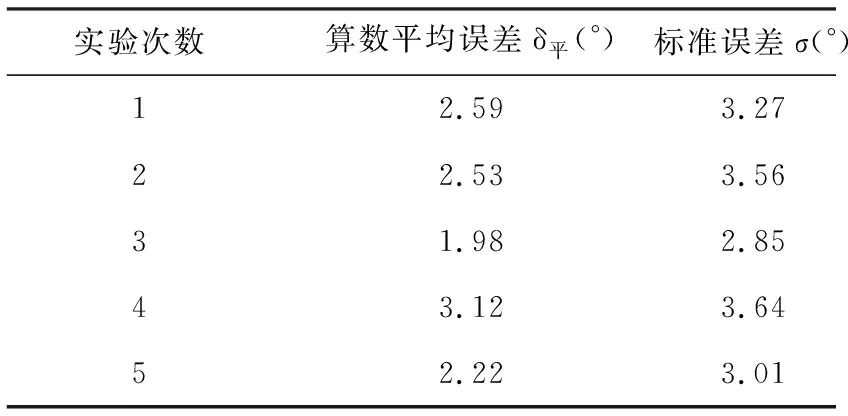
表2 基于逆运动学的误差计算结果

最大引用误差(又称允许误差)σmax，是测量值中的最大绝对误差与测量范围Y之比的百分数。

(16)

其中Y代表测量范围。得到逆运动学计算下肢关节角度髋关节允许误差σhip、膝关节允许误差σknee和踝关节允许误差σankle，见表3。

表3 逆运动学测量方法允许误差

综上分析，逆运动学方法计算出的最大算术平均误差δ平为3.12°，且具有小于10%的最大允许误差。

(2) 相关性分析是考察两个变量之间的线性关系的一种统计分析方法，更精确的说当一个变量发生变化时，另一个变量如何变化，对于逆运动学方法和向量方法同时测量一次下肢关节角度时，理论上如果二者的方法准确，那么其测量的数据应该是完全正相关的，这里使用SPSS软件计算Pearson相关系数[17]进行说明验证。

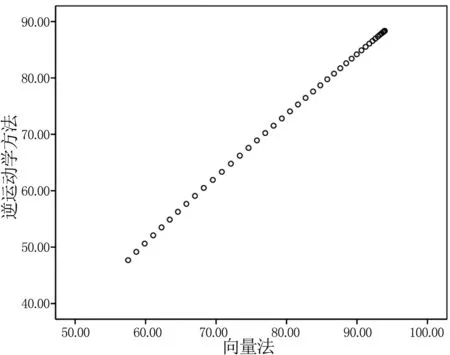
图7 逆运动学法与向量法的膝关节角度散点图

首先作出散点图大致判断一下，这里以膝关节角度为例，见图7，由散点图可以清晰的看出，二者呈明显的正相关。表4为通过SPSS软件进行Pearson相关性分析的结果。结果显示髋关节角度、膝关节角度和踝关节角度的计算，两种方法的相关性为0.998或0.999，并且在0.01水平上是显著相关的，换句话说具有99%的概率认为逆运动学法和向量法计算的角度存在着强正相关性。

决定系数是一个变量的方差可以被另一个变量的方差解释的百分比，其值为相关系数的平方，计算为99.6%和99.8%，因此，相关性越强说明一个变量可以更多的解释另一个变量表示的信息，即向量法的方差的99.6%或99.8%可以被逆运动学法来解释，0.4%的方差由其他原因导致。

表4 相关性分析结果

4.2 实际人体关节角度测量

通过人体骨骼模型试验说明，我们的实验方法能够测量模型的关节角度，我们在实际的人体下肢进行实验。实验中测试者穿戴设备进行反复抬腿动作，三维运动捕捉仪进行运动捕捉，得到原始数据后用编写的VC++程序进行处理，可以直接算出下肢关节角度。逆运动学计算的关节角度随时间变化的曲线图，见图8。

图8 逆运动学计算关节角度时间序列

以上数据算出的是符合人体下肢逆运动学建模的角度值，其中膝关节算出为负值，这主要是因为坐标系的关系引起的，其大小就是人体膝关节角度值。其次逆运动学算出的踝关节角度是图2中∠BCF，但是医学中踝关节角度为图2中标注的θAnkle，由几何关系就可以算出θAnkle。数据再进行处理后可以得到符合医学定义的下肢关节角度数据，见图9。

4.3 讨论与分析

基于逆运动学计算方法有效减少了需要点的数目，如果用固定在人体下肢向量来计算关节角度，3个杆需要用3个向量即至少5个虚拟点，如图4所示。基于逆运动学方法一侧腿只需要2个虚拟点，在实际应用时也增加了步态实验的方便程度，更能减少由于不可预知的点滑移导致步态评估不准确。

向量法误差主要来源于两个方面：(1)实际实验时，计算固定在大腿和小腿的向量共用一个点计算(股骨外髁，如图4)，但股骨外髁点根据经验不可能刚好标定在旋转中心处，从而导致误差，图10即为标记点计算出的大腿长度和小腿长度值，其大腿长度为定值而小腿长度出现变化。(2)固定在人体下肢的向量属于一条直线，但是人体下肢是有维度的，不能准确表现出下肢在长度维度的方向，具有较大误差。

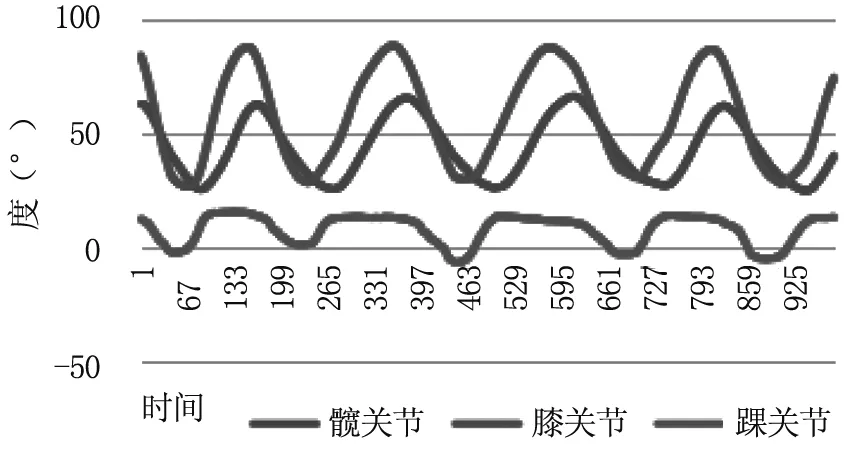
图9 医学定义关节角度序列

图10 标记点计算腿长数据

与逆运动学计算方法进行比较，对向量法进行误差分析，为了更加准确的通过向量法进行计算，分别在下肢刚体各固定两个标志点，这样就不会有共用标志点的误差了，误差来源主要都是向量表征人体下肢的误差。理论上人体直立姿态站立时，各个关节角度都是0度，但由于标记点偏差所计算出的角度非0。以人体大腿长度为450mm,小腿长度400mm，标记点最大偏移误差为20mm为误差计算模型(有研究表明，人体运动时标记点滑移最大可达30mm[18]，这里以20mm计算)，由此可以算出标记点误差导致的人体下肢关节角度的最大误差。髋关节为3.81°、膝关节为6.67°和踝关节2.86°，根据上述各个关节的旋转范围可以算出其最大允许误差，见表5。

向量误差计算具有比例特性，因此以上数据具有普遍性，数据表明，髋关节角度中向量法比逆运动学方法计算允许误差小，但向量法中膝关节由于受到大腿向量误差和小腿向量误差的双重影响其最大允许误差相对于逆运动学方法较大，踝关节角度计算二者方法误差水平相近。向量法如果考虑共用标记点的影响其误差可能更大，且不可预知。

表5 向量法测量方法允许误差

5 结束语

本研究提出的基于逆运动学计算下肢关节角度的方法具有小于10%的最大允许误差和3.12°的最大算术平均误差，误差主要来源于实验装置的设计和实验时参数的设定，如系统设置的脚刚体局部坐标系的Z轴不可能完全平行于脚底面(见图3)，再者由于髋关节、踝关节转角范围相对较小，分别为50°和35°，因此，得到最大允许误差相对较大，最大值为髋关节的9.8%。

本方法未计算人体下肢内、外翻及旋转角度的数据，因此，还具有改进空间，在该研究的实验后期，可以不断完善计算人体关节参数的机器人模型，如增加髋关节和踝关节的自由度等，制定一套符合原理的实验装置，完善脚上Marker点的固定方法，并增加其他的步态参数，包括步长、步速和步频等。未来测量步态只需要穿上脚刚体固定装置就可以完成整个的步态测量，方便实验人员采集多样本数据。本实验方法可以为步态与神经疾病的预警与评估研究提供实验基础[19-21]。