关于Pe11方程x2-3y2=1与y2-2nz2=16的公解

赵建红，万 飞

（1.丽江师范高等专科学校数学与计算机科学系，云南丽江674199；2.红河学院教师教育学院，云南蒙自661199）

关于Pe11方程x2-3y2=1与y2-2nz2=16的公解

赵建红1，万 飞2

（1.丽江师范高等专科学校数学与计算机科学系，云南丽江674199；2.红河学院教师教育学院，云南蒙自661199）

利用递归序列、奇偶分析、同余的性质和Pe11方程的解的性质等方法研究Pe11方程x2-3y2=1与y2-2nz2=16的公解的情况.

Pe11方程；整数解；公解

Pe11方程：

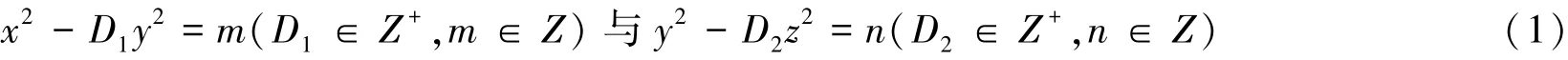
的公解问题一直受到人们的关注.目前结果大多集中在D2为正偶数上，D2为正奇数的结论目前尚不多见.m=n=1，D2为正偶数时方程（1）的公解的情况主要见文献［1-3］；m=1，n=4，D2为正偶数时时方程（1）的公解的情况主要见文献［4-11］.当k=1，m=16时方程（1）成为：

关于Pe11方程（2）的公解的情况，目前无相关结果.本文主要讨论D1=8，D2为正偶数时方程（2）的公解的情况.

定理1 设n∈Z+，2|n，则Pe11方程：

有且仅有一组平凡解（x，y，z）=（±7，±4，0）.

证明 因为Pe11方程x2-3y2=1的基本解为（7，4），则Pe11方程x2n-3y2n=1的全部正整数解为（xn+

容易验证以下性质成立：

（Ⅱ）y2n=2xnyn；

（Ⅲ）y2n+1≡4（mod 8）；

（Ⅳ）xn≡1（mod 2）；

（Ⅴ）gcd（xn，yn）=1，gcd（xn，xn+1）=1；

（Ⅵ）gcd（yn，yn+1）=4；

（Ⅶ）gcd（x2n，y2n+1）=gcd（x2n+2，y2n+1）=1；

（Ⅷ）gcd（x2n+1，y2n）=gcd（x2n+1，y2n+2）=7；

（Ⅸ）xn为平方数，当且仅当n=0.

设（x，y，z）=（xm，ym，z），m∈Z+为Pe11方程组（3）的正整数解，则由得：

若n为正偶数，设n=2k，k∈Z+，则由方程组（3）可得y2-22kz2=16，即得：

因为x，y，z∈Z+，所以（5）式可分解为以下两种情形：

或：

解（6）式得y=5，2kz=3，显然方程组无解；解（7）式得y=4，2kz=0，即Z=0.由此可得，若n为正偶数，方程组（3）有且仅有一组平凡解（x，y，z）=（±7，±4，0），无非平凡解，故n只能为正奇数，令n=2l-1，l∈Z+，则由（Ⅰ）知方程组（3）成为：

情形1 m为正偶数时，令m=2k，k∈Z+，此时式（8）成为：

由（Ⅲ）知，y2k-1≡y2k+1≡4（mod 8），4||y2k+1，4||y2k-1，则（9）式的右边的2的次数为4次，而 （9）式左边的2的次数为2l-1次，由此可知（9）式左右两端的2的次数不相同，即矛盾.由此可见，当m为偶数时，则（9）式无正整数解，所以方程组（3）无正整数解.

情形2 m为正奇数时，令m=2k-1，k∈Z+，此时方程（8）成为：

又由（Ⅱ）得y2k=2xkyk，y2（k-1）=2xk-1yk-1，则式（10）成为：

情形2.1 k为正奇数时，由（Ⅴ）知 gcd（xk-1，yk-1）=gcd（xk，yk）=1，gcd（xk-1，xk）=1；由（Ⅵ）知gcd（yk-1，yk）=4，则；由（Ⅶ）知gcd（xk-1，yk）=1；由（Ⅷ）知gcd（xk，yk-1）=7，则有，故两两互素且均不为1.

又k=1时，xk-1=x0=1；k=2时，；而对于，故k≠1时，两两互素且均不为1.

由（Ⅸ）知，xk-1为平方数当且仅当k=1，故k≠1时，xk-1不为平方数.由（Ⅳ）知，xk-1≡1（mod2）.又k≠1时，两两互素且均不为1，故k≠1时xk-1·不为平方数的2倍.所以4xk-1yk-1xkyk

k=1时，（11）式为22l-1z2=4x0y0x1y1=0，则z=0，故此时方程组（3）只有平凡解（x，y，z）=（±7，±4，0）.

情形2.2 k为正偶数时，由（Ⅴ）知，gcd（xk，yk）=1，gcd（xk-1，yk-1）=1，gcd（xk-1，xk）=1；由（Ⅵ）知gcd（yk-1，yk）=4，则由（Ⅶ）知gcd（xk，yk-1）=1；由（Ⅷ）知gcd（xk-1，yk）=7，则=1，故两两互素.不为平方数的2倍，所以此时式（11）无正整数解，则方程组（3）无正整数解.

又k=0时，xk=x0=1；k=2时，；而对于，故k≠0，2为正偶数时，两两互素且均不为1.

由（Ⅸ）知，xk为平方数当且仅当k=0，故k≠0时，xk不为平方数.由（Ⅳ）知，xk-1≡1（mod 2）.又k≠0，2为正偶数时两两互素且均不为1.故k≠0，2时，不为平方数的2倍，所以不为平方数的2倍，所以此时（11）式无正整数解，则方程组（3）无正整数解.

k=0时，（11）式为22l-1z2=4x-1y-1x0y0=0，则z=0，故此时方程组（3）只有平凡解（x，y，z）=（±7，±4，0）.

k=2时，（11）式为22l-1z2=4x1y1x2y2=4×7×4×97×56=27×72×97，则z=56，D=2×97≠22l-1，故此时方程组（3）只有平凡解（x，y，z）=（±7，±4，0）.

综上所述，定理1得证.

［1］ LJUNGGREN W.Litt om Simu1tane Pe11ske Ligninger［J］.Norsk Mat Tidsskr，1941，23：132-138.

［2］ PAN Jiayu，ZHANG Yuping，ZOU Rong.The Pe11 Equations x2-ay2=1 and y2-Dz2=1［J］.Chinese Quarter1y Journa1 of Mathematics，1999，14 （1）：73-77.

［3］ 乐茂华.关于联立Pe11方程方程组x2-4D1y2=1和y2-D2z2=1［J］.佛山科学技术学院学报（自然科学版），2004，22（2）：1-3.

［4］ 胡永忠，韩清.也谈不定方程组x2-2y2=1与y2-Dz2=4［J］.华中师范大学学报（自然科学版），2002，36（1）：17-19.

［5］ 管训贵.关于Pe11方程x2-2y2=1与y2-Dz2=4的公解［J］.华中师范大学学报（自然科学版），2012，46（3）：267-269.

［6］ 王冠闵，李炳荣.关于Pe11方程x2-6y2=1与y2-Dz2=4的公解［J］.漳州师范学院学报（自然科学版），2002，15（4）：9-14.

［7］ 贺腊荣，张淑静，袁进.关于不定方程组x2-6y2=1，y2-Dz2=4［J］.云南民族大学学报（自然科学版），2012，21（1）：57-58.

［8］ 杜先存，管训贵，杨慧章.关于不定方程组x2-6y2=1与y2-Dz2=4的公解［J］.华中师范大学学报（自然科学版），2014，48（3）：5-8.

［9］ 杜先存，李玉龙.关于Pe11方程x2-6y2=1与y2-Dz2=4的公解［J］.安徽大学学报（自然科学版），2015，39（6）：19-22.

［10］ 冉延平.不定方程组x2-10y2=1，y2-Dz2=4［J］.延安大学学报（自然科学版），2012，31（1）：8-10.

［11］ 过静，杜先存.关于Pe11方程x2-30y2=1与y2-Dz2=4的公解［J］.数学的实践与认识，2015，45（1）：309-314.

责任编辑：时 凌

责任编辑：时 凌

On the Common Solution of Pell Equations x2-3y2=1 and y2-2nz2=16

ZHAO Jianhong1，WAN Fei2
（1.Department of Mathematics and Computer Science，Lijiang Teachers Co11ege，Lijiang 674199，China；2.Co11ege of Teacher Education，Honghe University，Mengzi 661199，China）

By using recursive sequence，some properties of the odd and even，congruence and the so1utions to Pe11 equation，we study the common so1utions of Pe11 equations in the tit1e and find that the two equations have a common integer so1ution（x，y，z）=（±7，±4，0）.

Pe11 equation；integer so1ution；common so1ution

O156.1

A

1008-8423（2016）02-0146-03

10.13501/j.cnki.42-1569/n.2016.06.008

2016-06-10.

云南省教育厅科研基金（2014Y462）；红河学院校级课题（XJ15Y22）.

赵建红（1981-），男，硕士，副教授，主要从事数学教育及数论的研究；*

万飞（1969-），女，副教授，主要从事数学教育及初等数论的研究.