概率论中微积分思想的应用
张子颖,汪太月
(1东北大学 工商管理学院,辽宁 沈阳 110819;2湖北理工学院 数理学院,湖北 黄石 435003)
概率论中微积分思想的应用
张子颖1,汪太月2*
(1东北大学 工商管理学院,辽宁 沈阳 110819;2湖北理工学院 数理学院,湖北 黄石 435003)
概率论与微积分是数学中2个不同的分支,应用微积分中已有理论对概率论中的连续型随机变量的概率密度、分布函数、条件概率以及数学特征等进行探讨,充分体现了微积分思想在概率论应用中的重要作用,较好地实现了两者有机统一,为后续研究起到了铺垫作用。
微积分;概率论;极限;数学思想
概率论与微积分是数学的2个不同分支,概率论是研究随机现象统计规律的一门数学科学,微积分即采用极限这一工具对函数进行了很好地研究,微积分思想不仅贯穿于高等数学的整个学习当中,同时也是构建概率论大厦的基石[1].例如在映射作用下,集合被简化为随机事件,进而集合再被简化为实数,当样本空间被简化为实数集时,概率也相应由集函数近似成实函数.以函数的观点来衡量分布函数F(x),在概率论中,分布函数F(x)有着十分良好的性质,如单调有界、可积、几乎处处连续、几乎处处可导等[2],故高等数学中有关微积分的思想可以顺利地运用于概率论领域.连续型随机变量的分布函数、概率密度的表示以及期望、方差等都或多或少借鉴或运用了微积分的现有成果.再如概率论中运用极限论的地方也很多,如分布函数的相关性质、中心极限定理、大数定律、随机过程等[3].总而言之,微积分思想已经渗透到了概率论的各个方面,可以说若无微积分思想对概率论的推动,就不会有公理化和系统化的概率论,概率论也就不能形成数学的一个重要的分支[4].然而,概率论作为继高等数学后开设的一门课程,并非是高等数学的简单后继,而是对微积分思想的延伸,这也就开辟出一片崭新的数学天地.概率论的发展路径与高等数学有着很大的差别,概率论朝随机数学的方向前进,并成为随机数学的典型代表,有着和高等数学同等的地位,为古老数学学科注入了新鲜血液,使得数学能够与时俱进,从而进一步向前发展.
1 微积分思想在概率论中的应用
微积分主要包括微分学和积分学[5],虽然它和概率论是数学的2个不同分支,但是它与概率论有着紧密的联系.高等数学中有关函数方面的种种思想和方法可以广泛地运用于概率论领域.如随机变量的分布函数、概率密度的表示以及期望方差等,都或多或少借鉴或运用了微积分的现有成果.再如概率论中运用极限论的地方也很多,如分布函数的相关性质、中心极限定理、大数定律、随机过程等.下面将逐一体现微积分思想在概率论中的应用.
1.1泊松积分在概率论中的应用
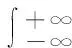
若随机变量X~N(μ,σ2)分布,利用泊松积分很容易计算随机变量的期望E(X)和方差D(X),已知正态分布的概率密度函数为:

根据期望及方差的定义有:
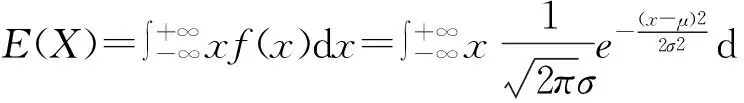
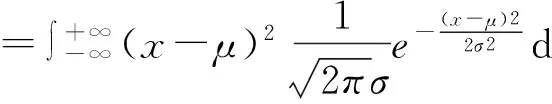
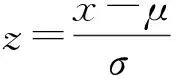


因为二维随机变量(X,Y)的联合概率密度函数为:
f(x,y)=

而(X,Y)关于X的边缘概率密度为:

由于:
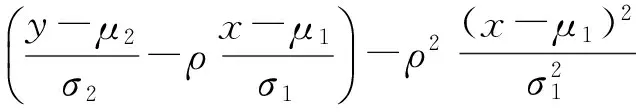
于是:


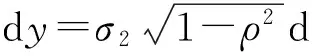
从而:

由泊松积分得:

同理有:

泊松积分在对数正态分布中同样也有应用,若随机变量X的函数Y=lnX服从正态分布N(μ,σ2),则称X服从参数为μ和σ2的对数正态分布.
设随机变量X服从参数为μ和σ2的对数正态分布.则利用泊松积分很容易求X的k阶原点矩.
令Y=lnX,由对数正态分布的定义知Y~N(μ,σ2),且X=eY,于是:
E(Xk)=E(ekY)

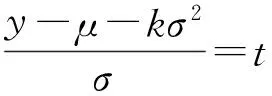

泊松积分在其他分布中同样也有很好的应用,设二维随机变量(X,Y)的概率密度为:
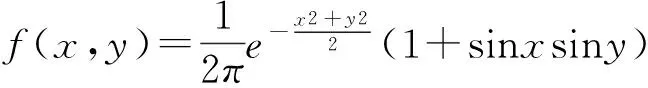
其中-∞ 所以: 其中-∞ 同理有: 泊松积分是微积分中的反常积分,它在概率论中的应用充分体现了微积分理理论同概率论的有机结合,下面进一步体现说明这一点. 1.2Γ(α)函数的指数分布中的应用 先来看Γ函数在指数分布的数字特征计算中的应用. 随机变量X服从参数为EXP(λ)的指数分布,其概率密度为: 1)连续随机变量X的数学期望为: 置换积分变量λx=t得Γ函数的特殊形式,即: 2)连续随机变量X的方差: D(X)=E(X2)-(EX)2= 积分做置换变量法积分化为Γ函数的形式,置换积分变量λx=t得: 3)连续随机变量X的k阶原点矩: (k=1,2,3,…). 4)连续随机变量X的k阶中心矩: 正态分布是概率论与数理统计中最常用的一类重要分布.而Γ(α)函数在正态分布的应用中起着重要作用.若随机变量X服从正态分布,那么计算随机变量X的k阶中心矩就要用到Γ(α)函数: 1) 当k是奇数时,因为被积函数是奇函数,所以积分等于零,可得到: μk(X)=0,k=1,3,5,…. 2)当k是偶数时,因为被积函数是偶函数,所以有: 置换积分变量t2=2μ,得: Γ函数不仅在处理指数分布的数字特征和计算正态分布的k阶中心矩中有着广泛应用,而且借助Γ函数,概率论中形成了一个很重要的-Γ分布.参数为α,λ(a>0,λ>0)的Γ分布的密度函数为: 当α=n∈N时,Γ分布Γ(α,λ)=Γ(n,λ)称为厄兰分布[6-7],它能够很好的运用于排队论和可靠性理论研究之中. 运用数学归纳法与卷积公式可证明Γ分布的可加性(再生性),即: 下面讨论当n=2时,Γ函数在概率论中的运用情况. 设ξ1~Γ(α1,λ),ξ2~Γ(α2,λ),且它们均相互独立,证明ξ1+ξ2~Γ(α1+α2,λ). 证由假设知ξi的概率密度函数为: 故只需求出ξ1+ξ2的概率密度函数为: 事实上根据卷积公式有: 令z-x=y 令y=zt,则: =zα1+α2-1B(α1,α2) 结论得证. x1+x2+…+xn~Γ(n,λ). 故有: 由以上的计算可以看出,应用微积分中的一些已知积分、级数性质等可以很好地简化概率论中数字特征的计算问题.不仅如此,微积分的基础思想——极限论也渗透到概率论中,在概率论中有广泛的应用. 1.3同阶数量级方法在概率论中的应用 考虑独立随机变量序列x1,x2,…,其中Xk的概率分布为: 试证明x1,x2,…,服从中心极限定理. 证明由期望及方差的定义可知: 所以: 由此可见,对任意的δ>0,当n→∞时, 从而由李雅普洛夫定理[2]知,x1,x2,…,服从中心极限定理. 1.4微增量法在概率论中的应用 在概率论中有一些随机事件的概率只依赖于一个变量的特点.虽然事件的概率是一个未知函数,但可以由事件的概率只依赖于一个变量的这一特性出发,通过微增量寻找等式,从而再通过求解微分方程的方法求出这个未知函数.具体步骤为:首先从这一个变量的局部性质出发(微增量),继而建立方程等式,最后应用微分方程的知识求出未知函数.下面举例说明. 某机器在△t时间内因故障而停止工作的概率为α△t+o(△t)(α为正常数).假设机器在不重叠的时间内停止工作的各个事件相互独立.已知机器在时刻t0正常工作,试求机器从时刻t0到t0+t这段时间内正常工作的概率. 在机器正常工作的情况下,所求概率只与时间区间[t0,t0+t]的长短有关,而与起点时刻t0无关.于是所求概率只与t有关,记为p(t).因为对函数p(t)的性质未知,且由题目条件知机器在任一时刻t的充分小的增量Δt时间内机器因故障而停止工作的概率为α△t+o(△t),故可先考查函数p(t)在微小增量△t时间内的变化特征.机器在[t0,t0+t+△t]内正常工作,当且仅当机器在[t0,t0+t]及[t0+t,t0+t+△t]这2段时间内均正常工作才成立.由题目假设可知这2 个事件相互独立,故有: p(t+△t)=p(t)p(△t)=p(t)[1-α△t-o(△t)], p(t+△t)-p(t)=-αp(t)△t-p(t)×o(△t), 因为p(t)≤1,故当△t→0,有: 求解微分方程得: p(t)=Ce-αt(C为任意常数)(*). 由题目假设知机器在t0时刻正常工作,于是由此知初始条件为p(0)=1,代入(*)式可求出C=1,得p(t)=e-αt,则机器从时刻t0到t0+t这段时间内正常工作的概率为e-αt.本例是概率论中求解概率的问题,但是其方法运用了微积分中极限的思维,显示出了微积分思想和概率论的紧密联系.当然,微分法在求解概率论中的期望和方差时也有巧妙的运用. 1.5逐项微分法在概率论中的应用 在概率论中离散型随机变量的数学期望及方差分别定义为: 连续型随机变量的数学期望及方差分别定义为: 当随机变量服从某一带参数的分布时,则由随机变量数学期望的定义,在求期望时可运用逐项微分法,先对等式两边同时关于参数求导,再根据微积分理论中的级数及积分的知识求出结果.而在求方差时,由于在前面的步骤中已求出数学期望E(ξ),由公式D(ξ)=E(ξ2)-[E(ξ)]2可知,现只需要求出随机变量ξ的二阶矩E(ξ2)即可.下面通过具体例子加以说明. 设随机变量X~p(λ),求E(X)与D(X). 由离散型随机变量分布律的完备性可得: 两边同时乘eλ得: 两边对λ求导且由幂级数的可交换性可得: 即:E(X)=λ. (**)式两边对λ求导得: E(X2)=λ+λ2,所以: D(X)=λ. 本研究运用微积分的思想对概率论作了简单探讨,如求期望、方差、概率密度函数等问题,当然,其在概率论中的应用远非于此,在建立完备的概率空间中也起了至关重要的作用.微积分是构建概率论理论的基石,在后续的工作中将运用微积分的思想对概率论作进一步研究,同时用概率论的相关结论来丰富微积分的思想. [1] 范玉妹,汪飞星,王萍,等.概率论与数理统计[M].2版.北京:机械工业出版社,2012:123-125. [2]沈恒范.概率论与数理统计教程[M].北京:高等教育出版社,2002:76-87. [3]张景中.趣味随机问题[M].北京:科学出版社,2004:6-33. [4]申若虹.模式识别中基于概率统计的Bayes算法分析[J].机械工程与自动化,2010(6):48-49. [5]吴传生.微积分[M].北京:高等教育出版社,2007:88-103. [6]同济大学数学系编.高等数学[M].7版.北京:高等教育出版社,2014:259-264. [7]汪太月,李宏伟,王志华.基于广义高斯分布的水印信号检测[J]. 数据采集与处理,2007,22(2):166-171 (责任编辑高嵩) Application of Calculus Idea in Probability Theory Zhang Ziying1, Wang Taiyue2* (1School of Business Administration,Northeastern University,Shenyang Liaoning 110819;2School of Mathematics and Physics,Hubei Polytechnic University,Huangshi Hubei 435003) Probability theory and calculus are two different branches of mathematics.In this paper,using the existing theories in calculus,the probability density,distribution function,conditional probability and mathematical characteristics of continuous random variables in probability theory are discussed,which fully reflects the important role of calculus in the application of probability theory,realizes the organic unity of the two and lays the foundation for the follow-up study. calculus;probability theory;limit;mathematical idea 2016-05-01 湖北省教育厅科研基金项目(项目编号:B2015095);湖北理工学院重大教研项目(项目编号:2015A08);湖北理工学院创新人才项目(项目编号:14xjz02C)。 张子颖,本科生。 汪太月,副教授,博士,研究方向:广义高斯信号处理、图像处理、信息安全。 10.3969/j.issn.2095-4565.2016.04.012 O211 A 2095-4565(2016)04-0048-06
























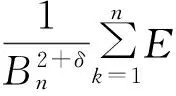






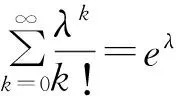
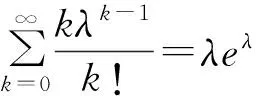
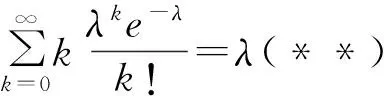


2 结论及展望

