一维连续随机变量概率密度估计
李 丛,吴传生*
(武汉理工大学,湖北武汉,430070)
一维连续随机变量概率密度估计
李 丛,吴传生*
(武汉理工大学,湖北武汉,430070)
摘要:由概率密度估计问题的定义可知概率密度估计问题可归结为概率分布函数的求导问题。将积分算子法应用于一维概率密度估计问题中,借助Taylor展开式得出基于积分算子法的概率密度估计;
关键词:概率密度估计;积分法
0 引言
模式识别、回归估计、概率密度估计是统计学习理论的三个基本问题。在解决学习问题的传统模式中,模式识别和回归估计都是建立在密度估计的基础之上。
在密度分布未知的情况下,我们需要通过已知的样本点数据对未知的分布进行估计,以达到预测概率密度的目的。大多数学者采用的密度估计方法主要分为两种:参数估计和非参数估计。非参数方法包括正态化方法,直方图方法、离散化方法、核方法、以及今年来人们将正则化方法应用到概率密度估计问题上产生的基于支持向量机的概率密度估计方法,以及基于TSVD方法的概率密度估计。
而上述提到的方法都只在一维情况下对概率密度估计问题进行了讨论,而对二维或高维的情况由于方法的限制或其他原因鲜有讨论。但在实际应用中概率密度所服从的分布是未知的,且在大多数情况下二维的随机变量相互之间并不是独立的,二维的随机变量的概率密度无法由两个一维随机变量的乘积得到,即f( x, y)≠f( x)•f( y )。所以只讨论一维的情况是不完全的。
本文将积分方法引入概率密度估计问题,将概率密度求解问题转化为数值微分问题,并提供了解决高维概率密度估计问题的新方法。
1 基于积分方法的一维概率密度估计
在进行概率密度估计之前,我们首先引入新的概率密度估计。

所以当样本个数足够大时,Fn(x )是总体分布函数F( x)的一个良好近似。

所以我们构造的经验分布函数Fn(x )具有如下性质:
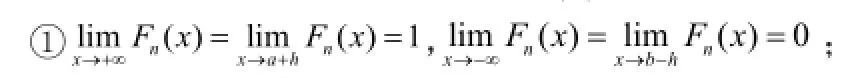
②Fn(x )为绝对连续函数;


但在实际情况中,由于样本量的限制,经验分布函数与真实分布函数之间必定存在差异,而这些微小的误差可能会造成数值结果的巨大误差。为了克服这种不稳定性,所以我们采用积分算子的方法,逼近F( x )的导数p( x)。
1.1一维数值微分的积分方法
假定f( x)∈Ck[ a, b],fδ(x)∈C[ a, b]且满足J( x)∈C[−1,1]为非负偶函数,∫1J( x) dx =1且满足J(i )(1)=J(i)(−1)=0,
−1i=0,1,2,…,k−1.满足以上条件的J( x)是存在的,比如取:

定义积分算子:

其中h>0为参数,r=1,2,…,k .(Drf)(x)可作为f(r)(x)的
h近似。
又由于概率密度估计的特殊性,我们只需要考虑经验分布的一次导数,即为我们的概率密度函数。因此

上式即作为我们的积分算子,其中F( x)为分布函数。
接下来,我们来介绍一维情况下积分算子对导函数的逼近效果。

而在概率密度估计问题中,由于样本量的限制,经验分布函数与真实分布函数间存在一定的差异,当经验分布函数与真实分布函数F之间满足如下条件时:

则有如下定理。
1.2概率密度函数性质的证明
众所周知,密度函数具有以下两个性质:
1)非负性的证明:

由于J( x)有良好的连续性,F( x )是绝对连续函数,且F′( x)勒贝格可积,所以根据勒贝格积分的分部积分公式可得:

由于J(1)=J(−1)=0,所以

又由于J( x)≥0恒成立,且F( x)为分布函数,满足右连续性且为非降函数,所以F′( x )>0恒成立。至此,非负性得证。
2)正则性的证明:

同样地,根据勒贝格分部积分法可得:

根据经验分布函数性质④我们可以得到:

2 总结
运用积分方法,笔者构造新的概率密度估计的正则化方法,将概率密度问题看作数值微分问题,很好的解决了一维情况下的概率密度估计问题。
同时积分方法也存在一定的缺陷,当样本量过大时,计算量将快速增加。下一步继续分析误差产生的原因,并对精度进行提高,同时寻找减小计算量的方法。
参考文献
[1]VLADIMIR NV.统计学习理论的本质[M].张学工,译.北京:清华大学出版社,2000:12-98
[2]George H. John, Pat Langley. Estimating Continuous Distributions in Bayesian Classifiers. In
Proceedings of the Eleventh Conference on Uncertainty in Artificial Intelligence, San Mateo, 1995.
[3] David W. Scott. Multivariate Density Estimation: Theory, Practice, and Visualization. New York, John Wile and Sons, 1992.
[4] J. Dougherty, R. Kohavi and M. Sahami. Supervised and Unsupervised Discretization of Continuous Features. ICML, 1995: 194-202.
[5] Emanuel Parzen. On Estimation of a Probability Density Function and Mode. Annals of Mathematical Statistics, 1962, 33(3): 1065-1076.
[6] 曹华孝等,一种基于改进W-SVM算法的概率密度估计[J].电子科技,第27卷第9期,2014年:40~43
[7] 吴笛,刘文.基于TSVD正则化方法的概率密度估计[J].武汉理工大学学报(信息与管理工程版).2012(01):60~63
[8] 黄小为,吴传生,高飞,高阶数值微分的积分方法[J].数学杂志,2008(04):431~434
作者简介
李丛(1990-),男,汉族,河北廊坊人,武汉理工大学硕士研究生,统计学基础研究
*通讯作者:吴传生(1957-),博士生导师,教授,研究方向:反问题、智能计算。
One-dimensional Continuous Random Variable Probability Density Estimation
Li Cong,Wu Chuangsheng
(Wuhan University of Technology, Wu han 430070,Hubei Province,China)
Abstract:According to definition of probability density estimation,probability density estimation can come down to the derivation of probability distribution function.The probability density estimation based on integral operator method using integral operator method into one-dimensional probability density estimation could be presented under the help of Taylor expanding.
Keywords:probability density estimation;integral method

