稳定渗流作用下出逸坡降的随机分析
罗显枫,李 昕
(1湖北理工学院 土木建筑工程学院,湖北 黄石 435003;2大连理工大学 建设工程学部,辽宁 大连 116023)
稳定渗流作用下出逸坡降的随机分析
罗显枫1,李昕2
(1湖北理工学院 土木建筑工程学院,湖北 黄石 435003;2大连理工大学 建设工程学部,辽宁 大连 116023)
利用局部平均(local average)法和协方差分解法生成的各向异性随机场来模拟单隔水板桩下的透水型地基土层的渗透系数的空间变异分布,并结合有限元法绘制出随机流网图,从而刻画出稳定渗流作用下的出逸坡降的统计特征,为实际工程风险评价提供科学依据。
局部平均法;各向异性随机场;稳定渗流;出逸坡降
0 引言
闸坝下游渗流出逸处,最容易发生流土、管涌之类的渗透破坏。造成这类事故的主要原因是渗流出逸坡降大于该处土料的临界坡降,因此设计人员必须严格控制渗流出逸坡降。国内学者也对此类问题展开了研究。沙金煊[1]推导了简单地下轮廓布置的出逸坡降计算公式。吴世余[2]提出了奇点附近渗透出逸坡降的测定方法。毛海涛[3]推导了无限深透水地基上土石坝坝基垂直防渗的出逸坡降计算公式。这些基于确定性土体的渗透系数计算工作有一定的理论价值。但是在实际工程中,由于土的渗透系数具有较大的空间变异性,采用传统的确定性方法计算得到的渗流出逸坡降不能为工程决策提供更精确的科学依据,因此本研究采用随机有限元方法进行渗流出逸坡降的仿真。具体做法为:利用局部平均法生成的各向异性随机场模拟单隔水板桩下的透水型地基土层的渗透系数的空间变异分布,并结合有限元法绘制出随机流网图,从而刻画出稳定渗流作用下的出逸坡降的统计特征,为实际工程风险评价提供依据。
1 随机场模型
1.1二维随机场的局部平均
土的工程特性依赖于空间土体的平均特性而非某一特定点的性质指标,所以考虑用随机场的局部平均进行随机有限元计算。随机场的单元A和单元A' 的相对位置图如图1所示,T1和T2分别为面积A水平和竖直方向尺寸。随机场X(t1,t2)在二维面积A=T1×T2上的局部平均可定义为[4]:
(1)
则在X为平稳随机过程时,XA的均值和方差分别计算如下:
E{XA}=μXA=E{X}=μX
(2)
(3)
式(3)中,
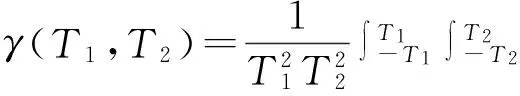
(4)
ρ(τ1,τ2)在本研究中取为各向异性的Markovian相关函数[5],可以写成:
(5)
式(5)中,θ1和θ2分别是随机场的水平和竖直方向的相关长度。

图1 随机场的单元A和单元A'的相对位置图
1.2协方差分解法
协方差分解法是一个数学概念最直接明了的生成随机场的方法。当利用它来生成局部平均随机场时,可采用下面两式获得:
Cn×n=Ln×nLn×nT
(6)
Cn×1=Ln×nWn×1T
(7)
Cn×n是把随机场离散成n个单元中任意2个单元(即局部平均后的随机变量XA,XA',如图1所示,T'1和T'2分别为面积A'水平和竖直方向尺寸)的协方差cov(XA,XA')构成的协方差矩阵;Gn×1是高斯随机场离散后的随机变量gi,i=1,2,…,n构成的向量。W是由n个独立且服从标准正态分布的随机变量构成的向量[6]。
1.3对数正态分布随机场
实际工程中认为土层渗透系数的概率分布应该服从对数正态分布,而在前述的随机场模拟中会产生一个离散的高斯正态随机场。因此,可将渗透系数的高斯随机场离散后的每一个正态随机变量转换成服从对数正态分布[7],即:
ki=exp(μlnk+σlnkgi)
(8)
式(8)中:ki是第i个单元的渗透系数;gi是渗透系数的高斯随机场的第i个单元的局部平均;μlnk和σlnk是渗透系数k的对数分布的均值和方差,分别可通过渗透系数的正态分布的均值μk和方差σk(变异系数为COVk)进行转换[8],即:
(9)
(10)
2 随机稳定渗流算例分析
2.1控制方程
本研究采用如下控制方程来描述单隔水板桩下的透水型地基土层渗流,即:
(11)
2.2算例介绍
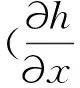
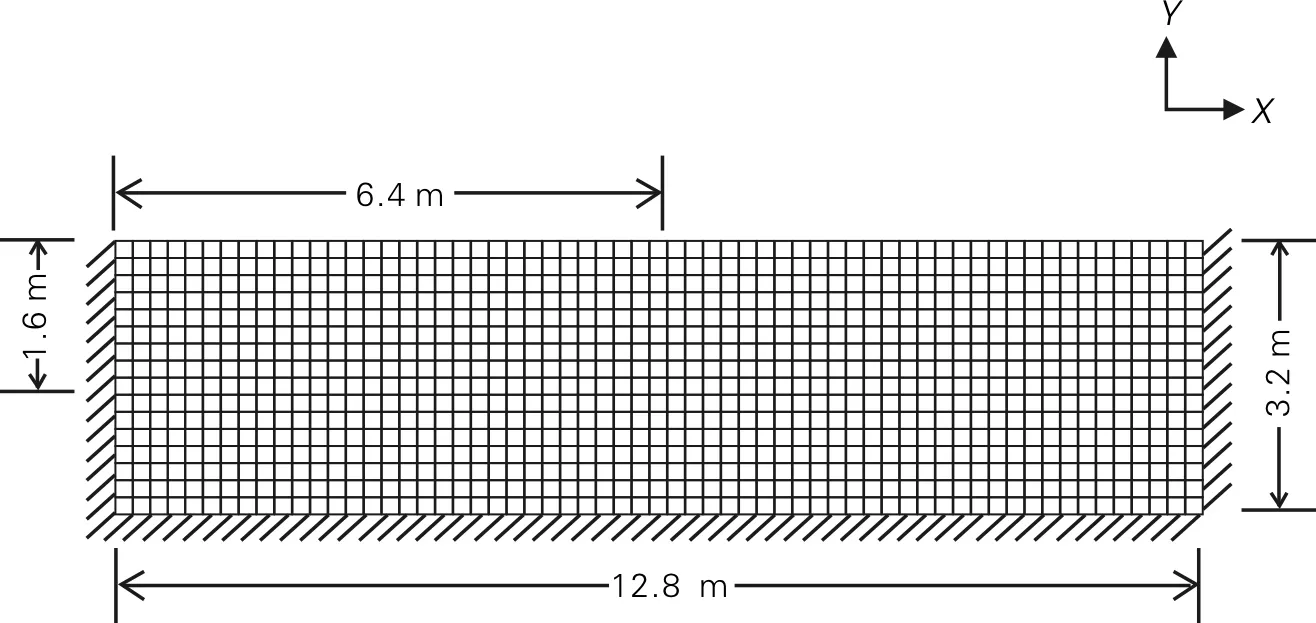
图2 有限元网格
2.3流网图
首先以渗透系数的均值μk=1×10-5m/s做确定性有限元分析,绘出流网图,确定性分析流网图如图3所示。在图3中,等势线的间隔值为0.05,等势线和流线相互正交。然后再以渗透系数的均值μk=1×10-5m/s、变异系数为1、随机场的水平方向和竖直方向θx=θy=1 m进行随机场仿真,绘出随机仿真的1次实现,如图4所示。在图4中,用灰度的变化来描述渗透系数的空间变异程度,颜色浅代表渗透系数大,颜色深代表渗透系数小,从图4中可以看到流线明显避开了颜色深的集中区域(即渗透系数小的集中区域),这同时也证明了本研究开发程序的正确性[11]。

图3 确定性分析流网图

图4 随机仿真的1次实现(包含流网图及渗透系数的空间变异分布)
2.4出逸坡降
在本例中首先以渗透系数的均值μk=1×10-5m/s做确定性有限元分析,ie的数值计算如图5所示。可根据2点数值微分方法计算出逸坡降idet=0.193(下标det代表确定性),这与该问题的解析解结果非常接近[12]。

图5 ie的数值计算
此外,为了研究渗透系数的空间变异性对出逸坡降均值mie的影响,这里保持渗透系数的均值μk=1×10-5m/s不变,让其变异系数COVk在[0.1,100]范围内变化,让竖直和水平方向相关长度比ζk=θy/θx分别等于1,2,4,8,16[13]。对这些不同工况分别进行随机有限元模拟,得到出逸坡降均值mie趋势图如图6所示。从图6中能看出当COVk趋近于0.1时,mie就已经逼近确定性分析结果idet=0.193。也就说明当COVk极小时,mie不受ζk的影响。当ζk=2时对应的mie曲线位置,基本一直高于ζk=1时对应的mie曲线位置;而当ζk=4,8,16时,各自对应的mie曲线的位置逐步下移。这说明渗透系数的竖直方向的相关长度增大有助于提高出逸坡降均值mie,同时必须满足竖直方向的相关长度要小于有限元模型的竖向长度3.2 m。

图6 出逸坡降均值mie趋势图
3 结论
本研究利用局部平均法和协方差分解法生成的各向异性随机场模拟单隔水板桩下的透水型地基土层的渗透系数的空间变异分布,并结合有限元法绘制出随机流网图,得到如下结论。
1)与确定性分析结果进行对比,发现在渗透系数的空间变异作用下,流线明显避开了渗透系数小的集中区域,而从渗透系数大的集中区域通过。
2)当渗透系数的变异系数COVk极小时,出逸坡降均值mie能逼近确定性分析结果,同时并不受随机场的竖直和水平方向相关长度比ζk的影响。
3)当随机场的竖直和水平方向相关长度比ζk逐步增大时,出逸坡降均值mie曲线不断上移,但是增大到一定数值之后,出逸坡降均值mie曲线开始不断下移。说明只有当随机场的竖直方向的相关长度小于有限元模型的竖向长度时,ζk的增大才有助于提高出逸坡降均值mie。
[1]沙金煊.闸坝地基下游渗流出逸坡降近似计算[J].江苏水利,1988(3):1-14.
[2]吴世余,赵殿信,张安家,等.奇点附近渗透出逸坡降的测定[J].水利水电技术,2001(10):7-9.
[3]毛海涛,侍克斌,李玉建.无限深透水地基上土石坝坝基垂直防渗的保角变换渗流计算[J].水利水运工程学报,2008(4):71-77.
[4]Vanmarcke E.Random fields:analysis and synthesis[M].World Scientific,2010:235-236.
[5]Zhu H,Zhang LM.Characterizing geotechnical anisotropic spatial variations using random field theory[J].Canadian Geotechnical Journal,2013,50(7):723-734.
[6]Davis MW.Production of conditional simulations via the LU triangular decomposition of the covariance matrix[J].Mathematical Geology,1987,19(2):91-98.
[7]Griffiths DV,Fenton GA.Three-dimensional seepage through spatially random soil[J].Journal of Geotechnical and Geoenvironmental Engineering,1997,123(2):153-160.
[8]Fenton GA,Griffiths DV.Statistics of free surface flow through stochastic earth dam[J].Journal of Geotechnical Engineering,1996,122(6):427-436.
[9]Griffiths DV,Fenton GA.Probabilistic analysis of exit gradients due to steady seepage[J].Journal of Geotechnical and Geoenvironmental Engineering,1998,124(9):789-797.
[10]Smith IM,Griffiths DV.Programming the finite element method[M].John Wiley & Sons,2005:326-327.
[11]Fenton GA,Griffiths DV.Risk assessment in geotechnical engineering[M].Wiley,2008:276-278.
[12]Lancellotta R.Geotechnical engineering[M].CRC Press,2008:227-230.
[13]Ahmed AA.Stochastic analysis of free surface flow through earth dams[J].Computers and Geotechnics,2009,36(7):1186-1190.
(责任编辑高嵩)
Stochastic Analysis of Exit Gradients Caused by Steady Seepage
Luo Xianfeng1,Li Xin2
(1School of Civil Engineering and Architecture,Hubei Polytechnic University,Hubei Huangshi 435003;2Faculty of Infrastucture Engineering,Dalian University of Technology,Dalian Liaonin 116023)
The anisotropic random field is generated by the local average method and covariance matrix decomposition method,which can be used to simulate the spatial variation of permeability of soil layers with a sheet pile.The Finite element method can be combined with the random field to draw the stochastic flow net,which can be used to reflect the statistic characteristics of exit gradients.The result of the calculation can provide scientific reference for practical engineering risk assessment.
local average method;anisotropic random field;steady seepage;exit gradient
2016-05-05
国家自然科学基金委创新研究群体基金项目(项目编号:51121005);湖北理工学院校级创新人才项目 (项目编号:13xjz01C)。
罗显枫,讲师,博士,研究方向:土木工程可靠度与风险控制。
10.3969/j.issn.2095-4565.2016.04.008
TV223.4
A
2095-4565(2016)04-0031-04

