基于LMI方法的不确定系统的保成本反同步
陈秀琴,张泽锋,沈志萍,李钧涛
(1信阳职业技术学院 数学与计算机科学学院,河南 信阳 464000;2河南师范大学 数学与信息科学学院,河南 新乡 453007)
基于LMI方法的不确定系统的保成本反同步
陈秀琴1,张泽锋1,沈志萍2,李钧涛2
(1信阳职业技术学院 数学与计算机科学学院,河南 信阳 464000;2河南师范大学 数学与信息科学学院,河南 新乡 453007)
针对一类具有不同参数摄动和外部干扰的不确定混沌系统,基于Lyapunov稳定性理论和线性矩阵不等式(LMI)方法,设计了一种线性状态反馈控制器使得从系统反同步到主系统,且确保了闭环成本函数值不超过规定的上限。同时通过求解矩阵不等式,得到了控制器的增益矩阵K。最后以Murali Lakshmanan Chua电路系统为例说明了该方案的有效性。
混沌系统;保成本反同步;线性矩阵不等式
0 引言
混沌系统是一种特殊的非线性系统,由于它对初值具有极度敏感性,混沌系统的同步曾一度被认为是控制界的难点.自从Pecora和Carrol[1-2]于20世纪90年代初首先提出用PC方法实现混沌系统同步后,混沌同步就已经引起了学者们的广泛关注,并随之出现了多种同步方法,如观测器方法[3-5]、滑模控制方法[6]、自适应设计方法[7]、反同步设计法[8-9]、LMI方法[10-13]等.
最近,江、郑[10]基于线性矩阵不等式理论提出了通过设计线性状态反馈控制器使得一类混沌系统同步.然而,文献[10]提出的标准没有考虑参数扰动和外部干扰.虽然仿真结果表明所提出的方法能降低外部噪声,但没有严格的数学证明.实际上,系统参数必然受到外力或其他因素的干扰.张和马[11]基于主动控制技术研究了一类受外部干扰和参数扰动的系统同步, 并给出了一个控制器,但是控制器设计的基础是主系统和从系统结构相同,而且没有给出有效的方法来找出增益矩阵.文献[12-13]虽然是基于LMI方法来研究系统的保成本控制,但他们是针对时滞系统来研究的.本研究受上述讨论的启发,对不确定混沌系统的参数和外部扰动时变的情况进行充分考虑,基于线性状态反馈技术和李雅普诺夫稳定性理论, 以确保系统保成本反同步.很容易验证通过求解LMI,建立保成本反同步,适用于一大类不确定混沌系统.最后,通过仿真验证了所提出的线性矩阵不等式条件的可行性.
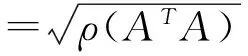
1 问题描述
假定有2个具有参数扰动和外部干扰的不确定混沌系统,其中主系统描述为:
(1)
从系统为:
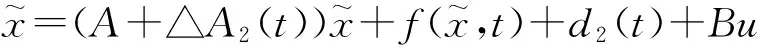
(2)

(3)
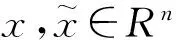
‖f(x,t)-f(y,t)‖≤L‖x-y‖
(4)
这里考虑的参数不确定性是假设为范数有界的形式:
[△A1(t)△A2(t)]=DF(t)[E1E2]
(5)
其中,D,E1和E2是已知常实数矩阵;F(t)∈Ri×j是一个未知的矩阵函数且勒贝格可测元素,满足:
FT(t)F(t)≤I
(6)
其中I表示单位矩阵.
此外,由于系统(1)是混沌系统的,所以存在一个正常数M1,使得‖x‖≤M1.
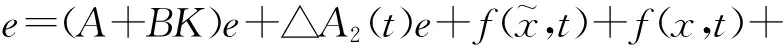
d2(t)+d1(t)+[△A1(t)-△A2(t)]x
(7)
与误差系统(7)相关的成本函数为:
(8)
其中,Q和R是正定对称矩阵;r是一个正常数,且:

本研究的目的是设计一个状态反馈控制器u(t)=Ke(t)使误差系统(7)保成本反同步.
引理1[14]对于任何相容维数矩阵D,E,F(t),当FT(t)F(t)≤I有下面的不等式成立:
DFE+ETFTDT≤εDDT+ε-1ETE.
2 主要结果
定理1考虑主系统(1)和从系统(2),如果(A,B)是可控矩阵,当反馈增益满足条件:
(9)
证明取李亚普诺夫函数为:
V=eTPe
(10)
则:

由引理1得:
(11)
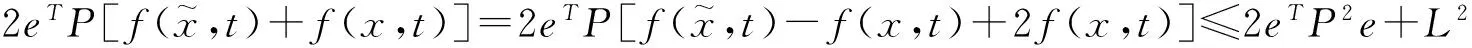
(12)
2eTP[d1(t)+d2(t)]≤eTP2e+d2
(13)
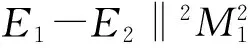
(14)
由式(9)和式(11)~(14)得:
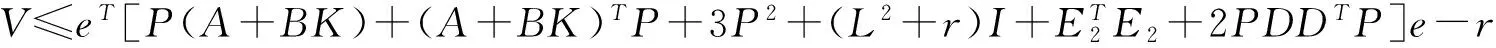
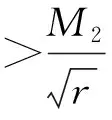
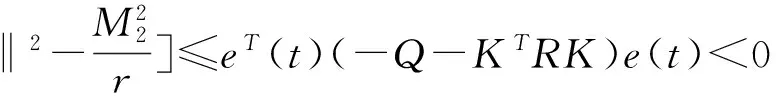
(15)
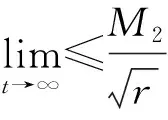
(16)
因为P为正定对称矩阵,所以eT(T)Pe(T)>0,即可得:
(17)
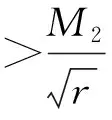
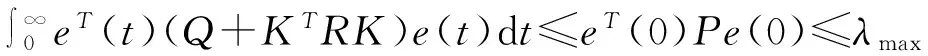
(18)
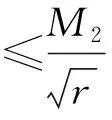
(19)
于是得出定理的结论是成立的.
定理2考虑主系统(1)和从系统(2),如果存在矩阵X>0,W满足下列不等式:
(20)
则设计状态反馈增益为K=WTX-1可以使系统保成本反同步,并且跟踪误差有界,
证明利用Schur补[14]的性质,式(9)可以转化为:
(21)
在式(21)两边同时乘以矩阵∧=diag(P-1,I,I,I,I,I),取X=P-1,K=WTX-1,则用定理1类似的方法可证得定理2结论成立.
3 数值模拟
混沌Murali Lakshmanan-Chua电路为:
(22)
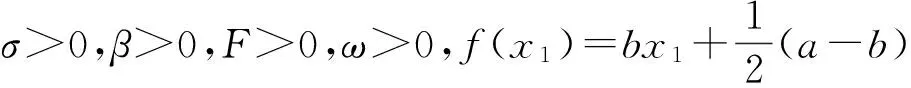
(23)
其中d1(t)=[0.28sin(0.5t),-0.2cos(5t)]T,△β1(t)=0.1cos(2t),△σ1(t)=-0.11cos(2t),从系统为:
(24)
其中,d2(t)=[-0.1cossin(5t)]T,△β2(t)=0.13cos(2t),△σ2(t)=0.098cos(2t).
由式(23)和式(24)得到:
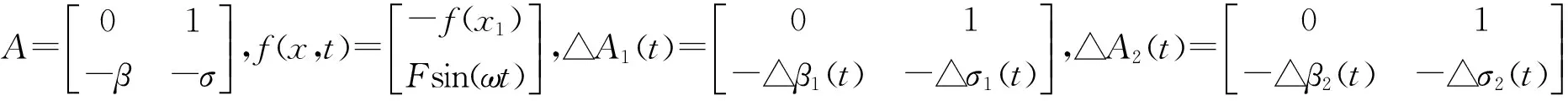
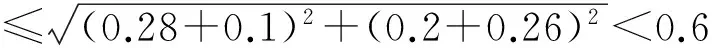
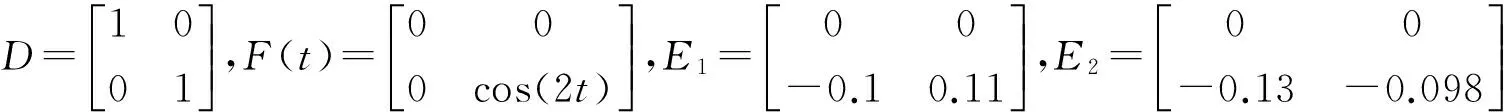
由方程(14)~(16)采用文献[16]的方法,可以将式(7)改写成:
(25)

由式(25)可以得到:
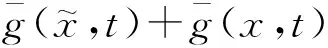


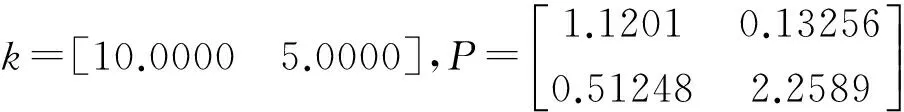
利用MATLAB的LMI工具箱得出仿真图如图1~4所示.
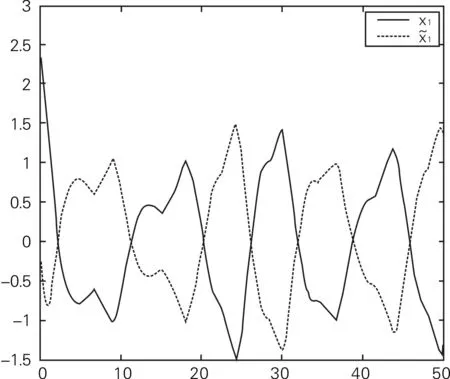
图曲线图
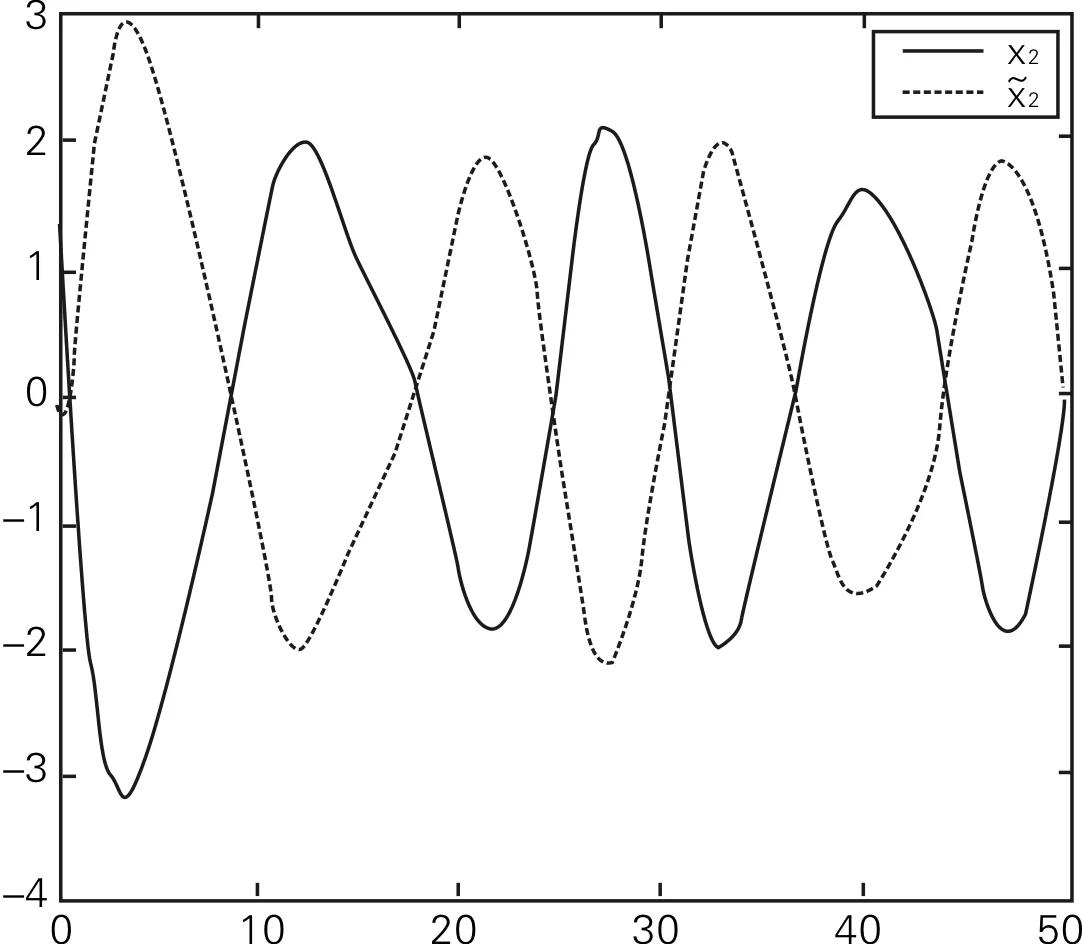
图曲线图

图3 e1(γ1),e1(γ2)

图4 e2(γ1),e2(γ2)
4 结论
研究了一类具有参数扰动和外界扰动的不确定系统的保成本反同步问题,基于Lyapunov稳定性理论和线性矩阵不等式(LMI)方法,设计了一种状态反馈控制器使从系统反同步到主系统,同时通过求解矩阵不等式,得到了控制器的增益,最后对Murali Lakshmanan Chua电路系统进行数值模拟,验证了本研究所提方法的可行性.
[1]Pecora LM,Carroll TL.Synchronization in chaotic systems[J].Physical Review Letters.1990,64(8):821-824.
[2]Chen G,Dong X.From Chaos to Order[J].Singapore:World Scientific,1998,31(2):113-122.[3]陈秀琴,沈志萍,李文林.具有噪声扰动的统一混沌系统的同步控制[J].电光与控制,2008,15(8):49-52.
[4]沈志萍,闫荣,邬依林.基于观测器的不确定混沌系统同步[J].电光与控制,2015,22(6):89-92.
[5]郑文娜,栾红霞,吕晶,等.状态观测器法实现改进的超混沌Lü系统同步[J].东北师大学报(自然科学版),2012,44(1):72-76.
[6]彭书华,李邓化,苏中,等.一类不确定混沌系统的模糊滑模控制与同步[J].计算机工程与设计,2010,31(6):1290-1293.
[7]李文林,刘振红,苗静.一类不确定混沌系统的自适应同步控制[J].电光与控制,2010,17(6):40-43.
[8]Li WL,Chen XQ,Shen ZP.Anti-synchronization of two different chaotic systems[J].Physica A.2008,387(14):3747-3750.
[9]吕翎,夏晓岚.非线性耦合时空混沌系统的反同步研究[J].物理学报,2009,58(2):814-818.
[10]Jiang GP,Zheng WX.An LMI criterion for linear-state-feedback based chaos synchrnization of a class of chaotic systems[J].Chaos,Solitons & Fractals.2005,26:437-443.
[11]Zhang H,Ma XK.Synchronization of uncertain chaotic systems with parameters perturbation via active control[J].Chaos Solitons and Fractals.2004,21:39-47.
[12]顾则全,刘贺平,廖福成,等.基于LMI的不确定时滞切换广义系统的保成本控制[J].系统工程与电子技术,2010,32(1):47-51.
[13]李阳.基于LMI的不确定离散多时滞系统保成本控制[J].辽宁石油化工大学学报,2012,32(4):83-87.
[14]俞立.鲁棒控制——线性矩阵不等式处理方法[M].北京:清华大学出版社,2002:16,48.
(责任编辑高嵩)
Guaranteed Cost Anti-synchronization for Uncertain Chaotic Systems Based on LMI Criteria
Chen Xiuqin1, Zhang Zefeng1,Shen Zhiping2,Li Juntao2
(1School of Mathematics and Computer Science,Xinyang Vocational and Technical College,Xinyang Henan 464000;2School of Mathematics and Information Science,Henan Normal University,Xinxiang Henan 453007)
For a class with different parameter perturbation and external disturbance of uncertain chaotic systems,based on the Lyapunov stability theory and linear Matrix Inequality(LMI)method,a linear state feedback controller is designed to make the slave system anti-synchroniz to the main system,and guarantee the closed-loop cost function value not to exceed the prescribed limit.At the same time,the controller gain matrix K is obtained by solving matrix inequalities.Finally,the scheme is expounded by taking Murali Lakshmanan Chua circuit system as an example.
chaotic system;guaranteed cost anti-synchronization;the linear matrix inequality (LMI)
2016-04-19
国家自然科学基金项目(项目编号:61203293);河南省重点科技攻关计划(项目编号:122102210131)。
陈秀琴,讲师,硕士。
10.3969/j.issn.2095-4565.2016.04.011
O231
A
2095-4565(2016)04-0043-05

