分数阶Genesio-Tesi系统的混沌及自适应同步*

刘晓君　洪灵

(西安交通大学 机械结构强度与振动国家重点实验室,西安　710049)



分数阶Genesio-Tesi系统的混沌及自适应同步*

刘晓君洪灵†

(西安交通大学 机械结构强度与振动国家重点实验室,西安710049)

对具有五次方非线性项的分数阶Genesio-Tesi系统的混沌及自适应同步进行了研究.首先分析了该系统平衡点的稳定性, 并发现该系统满足出现双涡卷混沌吸引子的必要条件.然后研究了在阶数相同和不同的两种情况下的吸引子以及系统随阶数变化的分岔情况.该系统在两种情况下存在混沌的最小有效维数分别为2.784和2.793.基于分数阶系统的稳定性理论，实现了该分数阶系统的自适应混沌同步.数值模拟验证了所设计的自适应控制器和未知参数的辨识观测器的有效性.

混沌,同步,分数阶系统,分岔,自适应控制

引言

分数阶微积分理论已有300多年的历史, 早期主要侧重于理论研究, 因没有实际的应用背景而发展十分的缓慢.1983年Mandelbort指出了自然界及许多科学领域中存在大量的分数维事实[1], 由此作为分形几何和分数维动力学基础的分数阶微积分取得了极大的进展[2].一直以来, 整数阶微积分都是研究的重点内容, 但整数阶微积分仅仅决定于函数的局部特征, 而分数阶微积分以加权的形式考虑了函数的整体信息, 在很多方面应用分数阶数学模型可以更准确地描述实际系统的动态响应.近几十年, 研究人员提出了很多的分数阶混沌系统, 例如分数阶Chua系统[3-5], 分数阶Duffing振子[6-7], 分数阶Chen系统[8], 分数阶Liu系统[9]等.

1990年, Pecora和Carroll提出完全同步以来[10], 混沌同步由于在保密通信等领域的潜在应用而得到了广泛的研究并取得了很多成果.常用的同步方法非常的多, 例如驱动响应同步法、自适应同步法、主动同步法以及反步法等[11-15].这些同步法是针对整数阶混沌系统, 随着分数阶系统的发展, 很多同步方法被应用到了分数阶系统.在实际情况中, 分数阶系统较整数阶系统更加具有普遍性, 而且具有更大的密钥空间, 因而对于分数阶混沌系统的同步研究具有重要的价值.

Genesio-Tesi系统是一个比较典型的混沌系统.该系统是由Genesio和Tesi基于谐波平衡法构造的[16], 具有混沌系统的很多特征, 并只包含了一个简单的平方项.Genesio-Tesi系统的混沌同步问题在文献[17]中得到了详细的研究.2005年, Lu提出了分数阶Genesio-Tesi系统[18], 并指出该系统出现混沌的最小有效维数为2.4.2012年, Faieghi等人通过主动同步法和滑模控制法实现了该分数阶系统的混沌同步[19].

研究了一个具有五次方非线性项的分数阶Genesio-Tesi系统的混沌和同步问题.在等阶和不等阶的情况下, 分别分析了该系统平衡点的稳定性, 系统随阶数变化的分岔情况.并得出了两种情况下, 系统出现混沌的最小维数分别为2.784和2.793.最后基于分数阶系统的稳定性理论,研究带有未知参数的分数阶Genesio-Tesi系统的自适应同步问题, 通过设计合适的控制器和未知参数辨识规则, 实现了该系统的自适应同步.数值模拟验证了所设计的控制器和参数辨识规则的有效性.

1　系统描述

具有五阶非线性项的分数阶Genesio-Tesi系统描述如下：

(1)

其中x,y,z为系统状态变量,b1,b2,b3,b4为系统参数,q1,q2,q3为分数阶导数的阶数.

E1(l1=0.5109,l2,3=-0.4055±1.9365i)

E2,3(l1=-1.5053,l2,3=0.6027±2.2251i)

从特征值可以看出, 平衡点E1是指数1的鞍点,其它的两个平衡点为指数2的鞍点.对于混沌系统, 涡卷只能在指数2的鞍点附近产生.指数1的平衡点的作用是连接两个涡卷.所以系统(1)满足产生双涡卷的必要条件[20-21].

1.1阶数相等的情况

当系统的阶数相等时, 即q1=q2,q3=q, 系统的参数取为b1=-2,b2=3.5,b3=0.3,b4=-1, 阶数为q=0.95.系统平衡点的稳定性可以通过计算其对应的特征根来研究, 平衡点E1的特征方程为:

det(diag([lmqlmqlmq])-J)

=l285+0.3l190+3.5l95-2=0

(2)

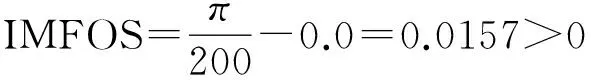
det(diag([lmqlmqlmq])-J)

=l285+0.3l190+3.5l95+8=0

(3)

为了更好的研究系统(1)的动力学行为, 以分数阶导数的阶数做为控制参数, 通过数值仿真, 得到当阶数q∈[0.88,0.97]时系统的分岔图, 如图2所示.从图中可以看到, 系统发生了倍周期分岔和内部激变, 其中内部激变在q=0.953时发生, 表现为系统的吸引子从单涡卷到双涡卷的变化, 如图3所示.同时可得系统在等阶情况下, 产生混沌的阶数为q=0.928 , 则系统产生混沌的最小维数为2.784.

图1　系统(1)在三维空间中的混沌吸引子Fig.1　The chaotic attractor of system (1) in 3D phase space

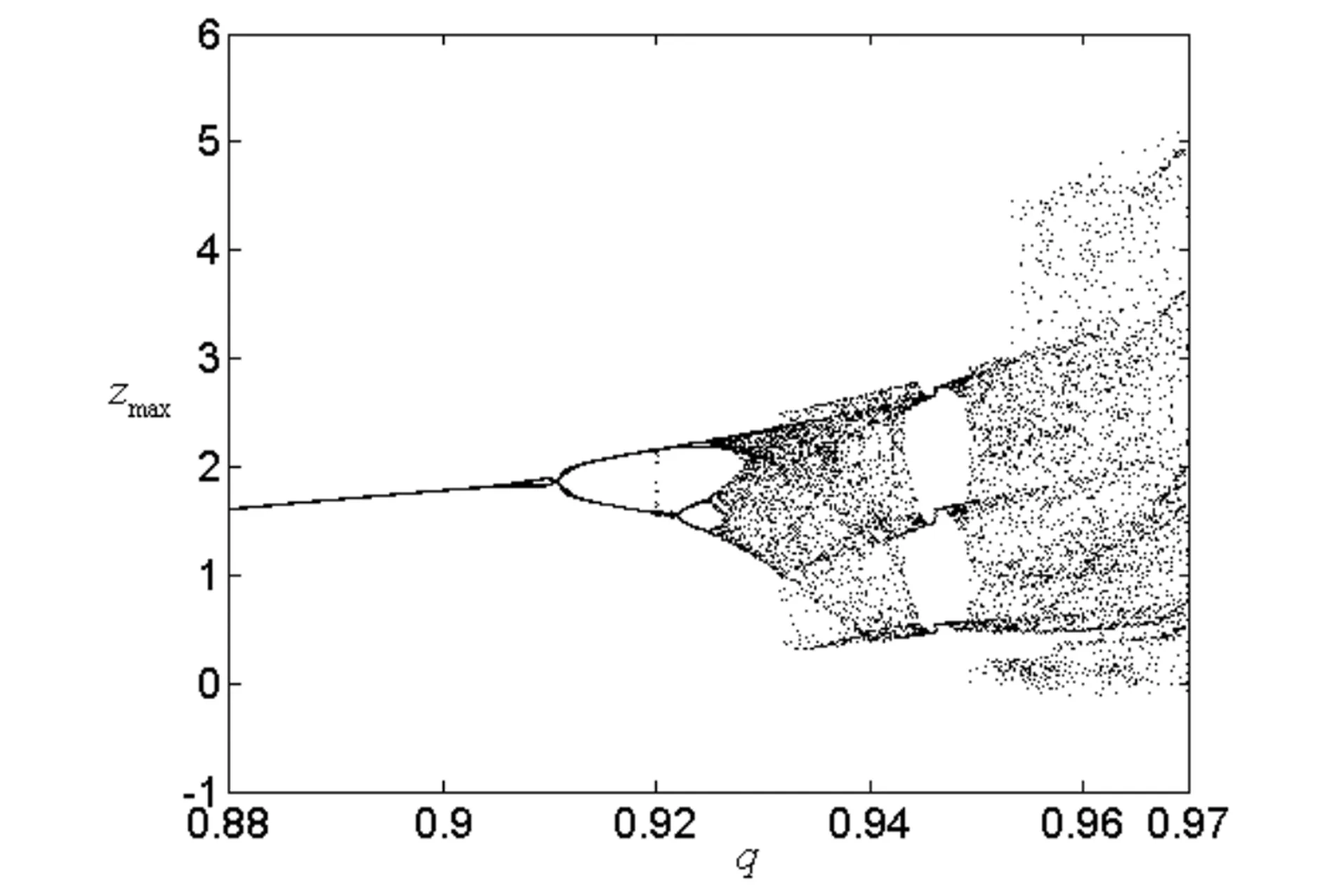
图2　系统(1)在等阶情况下随阶数q变化的分岔图Fig.2　Bifurcation diagram of the system (1) with order q

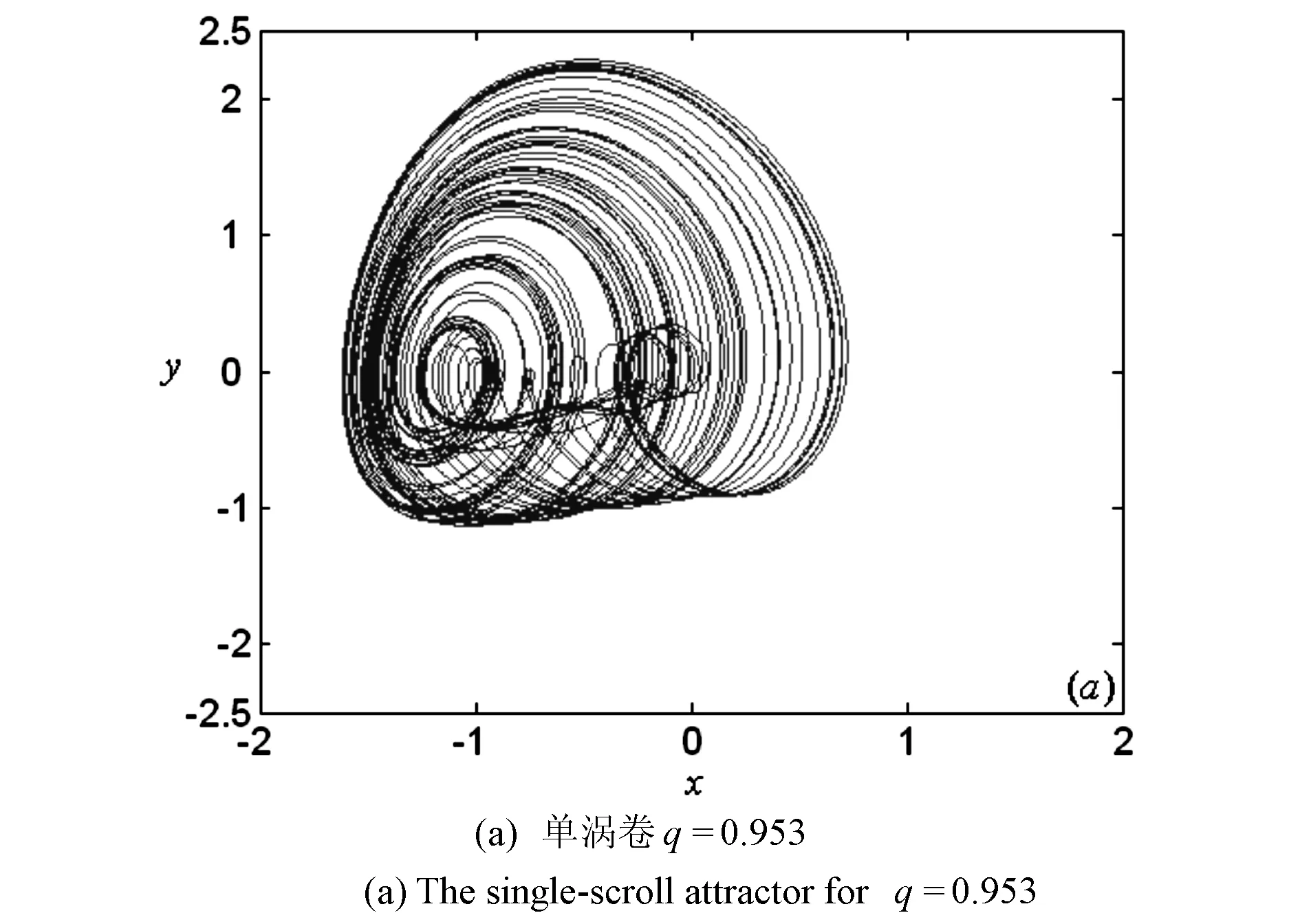
图3　系统在不同阶数的x-y平面上吸引子Fig.3　The attractors in x-y phase plane for different orders

1.2阶数不相等的情况

在这种情况下, 取q1=0.95,q2=0.97,q3=0.95, 系统平衡点的稳定性可以通过计算其对应的特征根来研究, 平衡点E1的特征方程为:

det(diag([lmq1lmq2lmq3])-J)

=l287+0.3l192+3.5l95-2=0,

(4)

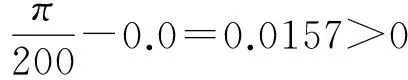
det(diag([lmq1lmq2lmq3])-J)

=l287+0.3l192+3.5l95+8=0,

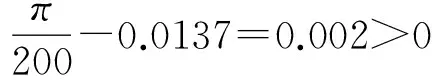
为了获得系统(1)在不等阶的情况下产生混沌的最小有效维数, 令q1=q2=1, 数值仿真得到当q3≥0.822时, 系统为混沌态.同样可以得到当其中两个阶数值为1时, 系统产生混沌态的条件分别为q2≥0.824和q1≥=0.793.因此, 系统的最小有效维数为2.793.

同样通过分岔图来分析系统随阶数变化的动力学行为, 数值仿真得到系统随阶数q3变化的分岔图,其中变化范围为q3∈[0.85,0.97],如图4.从图中可以看到, 除了在q3∈[0.85,0.874]和q3∈[0.92,0.93]时, 系统发生了倍周期分岔外.系统一直处于混沌状态, 并且在q3=0.938时, 混沌区域突然变宽, 即系统发生了内部激变.吸引子为从单涡卷到双涡卷的变化, 如图5所示.

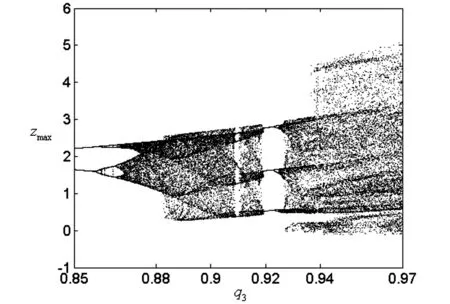
图4　系统(1)在不等阶情况下随阶数q3变化的分岔图Fig.4　Bifurcation diagram of the system (1) with order q3

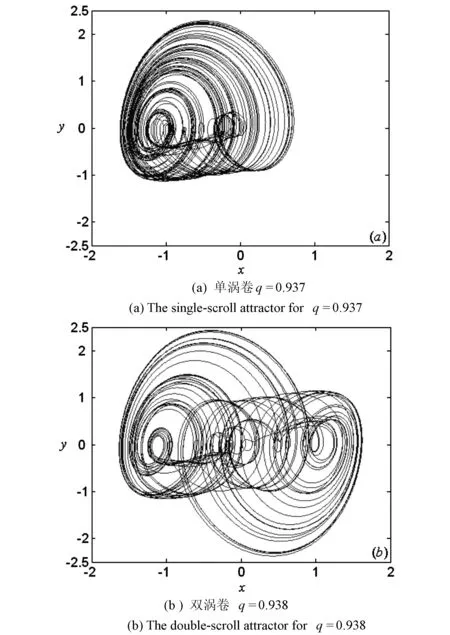
图5　系统在不同阶数的x-y平面上吸引子 Fig.5　The attractors in x-y phase plane for different orders

2　系统(1)的自适应同步

在这一节中, 利用反步法来研究系统(1)的自适应同步.以系统(1)作为驱动系统, 并将其改写为如下形式:

(6)

其中参数均为未知的.响应系统为如下形式:

(7)

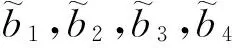
(8)

定理1当自适应控制器和参数辨识规则分别设计为如下形式时, 驱动系统(6)和响应系统(7)达到同步.

(9)

(10)

证明：将自适应控制器(9)代入误差系统(8),则可得误差系统

(11)

结合上式和(10), 可得：

=A(e1,e2,e3,eb1,eb2,eb3,eb4)T

(12)

其中

假定λ为矩阵A的一个特征根,且该特征值所对应的非零的特征向量为

ζ=(ζ1,ζ2,ζ3,ζ4,ζ5,ζ6,ζ7)T

则

Aζ=λζ

(13)

通过对上式两端进行共轭转置运算H,可得

(14)

式(13)左乘1/2ζH,同时式(14)右乘1/2ζ,所得结果相加得到

(15)

进一步化简

(16)

将矩阵A代入上式,得到

(17)

其中

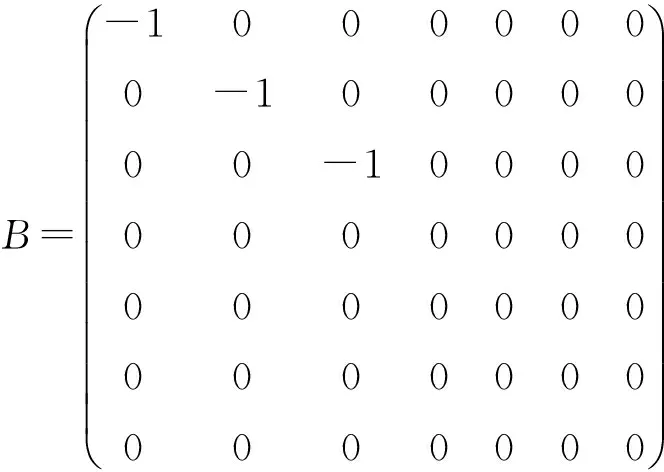
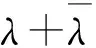
(18)

根据分数阶系统的稳定性理论，则误差动力系统(12)的平衡点渐进稳定.因此

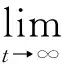
(19)

这说明驱动系统(6)和响应系统(7)达到了同步,证毕.

图6　系统(6)与(7)的同步误差曲线Fig.6　The curves of the synchronization errors of the systems (6) and (7)

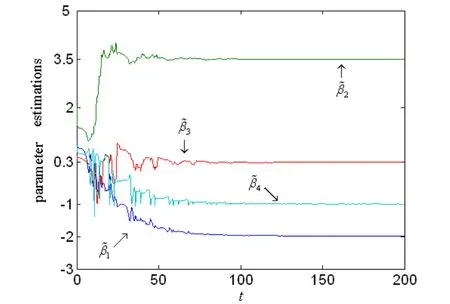
图7　未知参数的辨识曲线

取参数的真实值分别为b1=-2,b2=3.5,b3=0.3,b4=-1, 阶数为q1=q2=q3=0.95.驱动系统和响应系统的初值分别取为(-0.2,0.5,0.2)和(0.5,1,-1).数值仿真,得到系统的同步误差曲线(如图6)和未知参数辨识曲线(如图7),可以看到随着时间t→200,误差趋近0,同时未知参数的估计值趋向其真实值,驱动系统和响应系统达到了同步,说明所设计的同步控制器和未知参数辨识规则是有效的.

3　结论

对具有五次方非线性项的分数阶Genesio-Tesi系统的混沌及自适应同步进行了研究.分析了该系统平衡点的稳定性, 并发现该系统满足出现双涡卷混沌吸引子的必要条件.然后研究了在阶数相同和不同的两种情况下的吸引子以及随系统阶数变化的分岔情况.并得出了该系统在两种情况下存在混沌的最小有效维数分别为2.784和2.793.最后，通过基于分数阶系统的稳定性理论,实现了该分数阶系统的自适应混沌同步.数值模拟验证了所设计的自适应控制器和未知参数的辨识观测器的有效性.所得结果为该分数阶系统在保密通信中的应用提供了基础数据.

1Mandelbort B B. The fractal geometry of nature. New York: W.H. Freeman,1983

2Lorenz E N. Deterministic nonperiodic flow.JournaloftheAtmosphericSciences, 1963, 20(130): 130～141

3Hartley T T, Lorenzo C F, Qammer H K. Chaos on a fractional Chua′s system.IEEETrans.CircuitSystemFundationTheoryApplication, 1995, 42(8): 485～490

4Li C P, Deng W H, Xu D. Chaos synchronization of the Chua system with a fractional order .PhysicaA, 2006,360(2):171～185

5Zhu H, Zhou S B, Zhang J. Chaos and synchronization of the fractional-order Chua′s system.ChaosSolitions&Fractals, 2009,39(4):1595～1603

6廖少锴, 张卫.分数阶Duffing振子的动力学研究. 动力学与控制学报, 2008, 6 (2): 122～124 (Liao, S.K, Zhang, W. Dynamics of fractional Duffing oscillator.JournalofDynamicsandControl, 2008, 6(2): 122～124 (in Chinese))

7Gao X, Yu J. Chaos in the fractional order periodically forced complex Duffing′s oscillators.ChaosSolitions&Fractals, 2005, 24(4): 1097～1114

8Lu J G, Chen G R. A note on the fractional-order Chen system.ChaosSolitions&Fractals, 2006, 27(3): 685～6889Gejji V D, Bhalekar S. chaos in fractional ordered Liu system.Computers&MathematicswithApplications, 2010, 59(3): 1117～1127

10Pecora L M, Carroll T L. Synchronization in chaotic systems.PhysicalReviewLetter, 1990,64: 821～824

11Yan J J, Chang W D, Hung M L. An adaptive decentralized synchronization of master-slave large-scale systems with unknown signal propagation delays.ChaosSolitons&Fractals, 2006, 29(2): 506～513

12Odibat Z M. Adaptive feedback control and synchronization of non-identical chaotic fractional order systems.NonlinearDynamics, 2010, 60(4): 479～487

13Agrawal S K, Srivastava M, Das S. Synchronization of fractional order chaotic systems using active control method.ChaosSolitons&Fractals, 2012, 45(6): 737～752

14Yu Y G, Zhang S C. Adaptive backstepping control of uncertain Lu system.ChinesePhysics, 2002, 11(12): 1249～125315胡建兵, 韩焱, 赵灵东. 一种新的分数阶阶系统稳定理论及在back-stepping方法同步分数阶混沌系统中的应用. 物理学报, 2009, 58(4): 2235～2239 (Hu J B, Han Y, Zhao, L D. A novel stability theorem for fractional systems and its applying in synchronizing fractional chaotic system based on back-stepping approach.ActaPhysicaSinica, 2009, 58(4): 2235～2239 (in Chinese))

16Genesio R, Tesi A. Harmonic balance methods for the analysis of chaotic dynamics in nonlinear systems.Automatica, 1992,28 (3): 531～548

17Chen M Y, Han Z Z, Shang Y. General synchronization of Genesio-Tesi systems.InternationalJournalBifurcationandChaos, 2004,14(1): 347～354

18Lu J G. Chaotic dynamics and synchronization of fractional-order Genesio-Tesi systems.ChinesePhysics, 2005, 14 (8): 1517～1521

19Faieghi M R, Delavari H. Chaos in fractional-order Genesio-Tesi system and its synchronization.CommunicationsinNonlinearScienceandNumerical.Simulation, 2012, 17(2): 731～741

20Tavazoei M S, Haeri M. A necessary condition for double scroll attractor existence in fractional-order systems.PhysicsLettersA, 2007, 367(1): 102～113

21Zeng C B, Yang Q G, Wang J W. Chaos and mixed synchronization of a new fractional-order system with one saddle and two stable node-foci.NonlinearAnalysis-RealWorld, 2011, 65(4): 457～466

*The project supported by the National Natural Science Foundation of China (11172224)

† Corresponding author E-mail: hongling@mail.xjtu.edu.cn

27 June 2013,revised 28 February 2014.

CHAOS AND ADAPTIVE SYNCHRONIZATION IN FRACTIONAL-ORDER GENESIO-TESI SYSTEMS*

Liu XiaojunHong Ling†

(StateKeyLaboratoryforStrengthandVibrationofMechanicalStructures,Xi′anJiaotongUniversity,Xi′an710049,China)

The chaos and adaptive synchronization for a fractional-order Genesio-Tesi system with fifth order nonlinearity were investigated. The stability of equilibrium points was studied, and the necessary condition for double-scroll attractor existence in the system was satisfied. The bifurcation and an interior crisis from single-scroll to double-scroll attractors were also found with the variation of derivative order. The minimum effective dimension for the system to remain chaos is 2.784 in commensurate-order case and 2.793 in incommensurate-order case. Furthermore, the adaptive synchronization of the system with uncertain parameters via back-stepping approach was realized by designing appropriated controllers. Numerical simulations were carried out to demonstrate the effectiveness and flexibility for the controllers.

chaos,synchronization,fractional-order systems,bifurcation,adaptive control

E-mail: hongling@mail.xjtu.edu.cn

10.6052/1672-6553-2016-09

2013-06-27收到第1稿,2014-02-28收到修改稿.

*国家自然科学基金资助项目(11172224)