铰支柔性梁主参数共振的时滞反馈控制*

彭剑　张改　李禄欣

(湖南科技大学土木工程学院, 湘潭　411201)



铰支柔性梁主参数共振的时滞反馈控制*

彭剑†张改李禄欣

(湖南科技大学土木工程学院, 湘潭411201)

研究了时滞反馈控制作用下铰支柔性梁主参数共振问题.采用多尺度法,从理论上推导了时滞位移反馈控制作用下铰支柔性梁非线性主参数共振,分析了时滞、反馈控制增益,非线性系数等系统参数对系统非线性主参数振动的影响,分析了主参数动力响应随参数变化的规律.结果表明:随着反馈增益的增大,系统响应幅值得到明显抑制,合理地控制系统参数选取可提高振动控制的效率.

时滞反馈,主参数共振,柔性梁,振动控制,稳定性

引言

动力系统在本质上是非线性或趋于在一定条件下的非线性,源于非线性项的影响,系统存在极限环、跳跃现象,分岔及混沌等.在实际工程中,柔性梁的非线性动力学及分岔研究、横向激励作用下柔性梁的大幅振动控制是重要研究内容之一,采用时滞反馈控制技术也引起了广泛关注.

Hegazy[1]采用三次非线性策略对单模态柔性梁进行振动控制.冯志宏和霍睿[2]基于加速度时滞闭环反馈控制策略,研究了压电耦合悬臂梁的时滞反馈控制及稳定性.陈龙祥和蔡国平[3]对旋转运动柔性梁的时滞主动控制开展了实验研究,得到控制系统中的时滞也有可利用的价值.赵艳影和徐鉴[4]研究了时滞非线性动力吸振器的减振机理,通过调节反馈增益系数和时滞来实现主系统的减振.Daqaq等[5]采用时滞加速度反馈控制研究了压电耦合悬臂梁的非线性振动.刘铭等[6]对中立型时滞反馈扭转控制系统的稳定性进行了分析.贾雁兵, 等[7]研究了异质性和时滞作用下神经元网络的共振动力学.王在华和胡海岩[8]对时滞系统研究进展作了系统的综述.

本文研究了时滞反馈控制对铰支-铰支柔性梁非线性动力响应的影响.运动方程具有平方阻尼、三次和五次非线性及参数激励项.采用多尺度法求解该非线性方程.该系统采用线性时滞位移反馈控制,以幅频响应曲线和时程曲线反映其控制效果,分析了不同控制参数对系统主参数振动的影响.

1　振动控制模型

图1给出了轴向激励作用下长度为l的两端铰支柔性梁的物理模型.轴向激励作用下铰支梁的横向位移w(x,t)的运动微分方程表示如下[9]:

(1)

其中:一撇表示对x求导,m表示梁的线重,E是弹性模量,I为惯性矩,c是阻尼系数.边界条件如下:

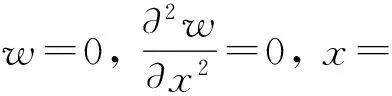
(2)

运用Galerkin方法对位移函数w(x,t)进行展开:

(3)

f2qn3cosΩt-α1qn3-α2qn5)=Tn

(4)

Tn=-knqn(t-τ)

(5)

kn为控制增益,τ为时滞.

图1　轴向激励下的铰支柔性梁的理论模型Fig. 1　Theoretical model of a hinged-hinged flexible beam subjected to harmonic axial excitation

2　非线性响应:主参数共振

采用多尺度法[10]对主参数共振进行计算.令Ω=2ω0+εσ,σ=Ο(1).将方程(4)的解记为:

qn(t)=qn0(T0,T1)+εqn1(T0,T1)+…

(6)

式中T0=t,T1=εt,同时设:

f1qncosΩt=f1qncos(2ω0T0+σT1),

f2qn3cosΩt=f2qn3cos(2ω0T0+σT1)

(7)

将方程(6-7)代入方程(4)中,令两端的ε0和ε1的系数相等,得到:

D02qn0+ωn2qn0=0

(8)

D02qn1+ωn2qn1=-2D0D1qn0-μ1D0qn0-

μ2(D0qn0)D0qn0-f1qn0cosΩt-f2qn03cosΩt+

α1qn03+α2qn05-knqn0(T0-τ,T1)

(9)

方程(8)的通解可以写为:

qn0=An(T1)exp(iω0T0)+

(10)

将qn0代入方程(9)中,并把cos(2ω0T0+σT1)用复数形式表示,有:

exp(iω0T0)-μ2ω02An2exp(2iω0T0)-

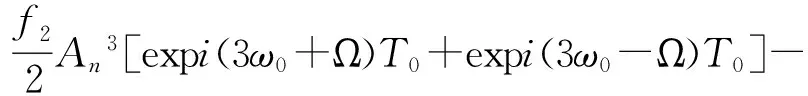
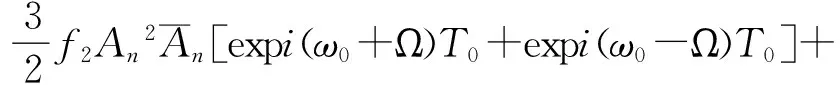
(11)

其中cc代表前面各项的共轭复数.消去方程(11)中的久期项,有:

(12)

将An表示成极坐标形式:

(13)

式中an和βn都是实函数,分离实虚部,可得:

(14)

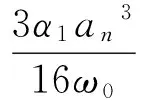
(15)

的解,这两个方程取平方后相加,得到:

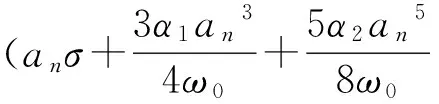
(16)

上式即主参数共振的幅频响应方程.

3　算例分析

本节主要讨论时滞、控制增益及非线性系数对主参数振动第一阶模态响应的影响.

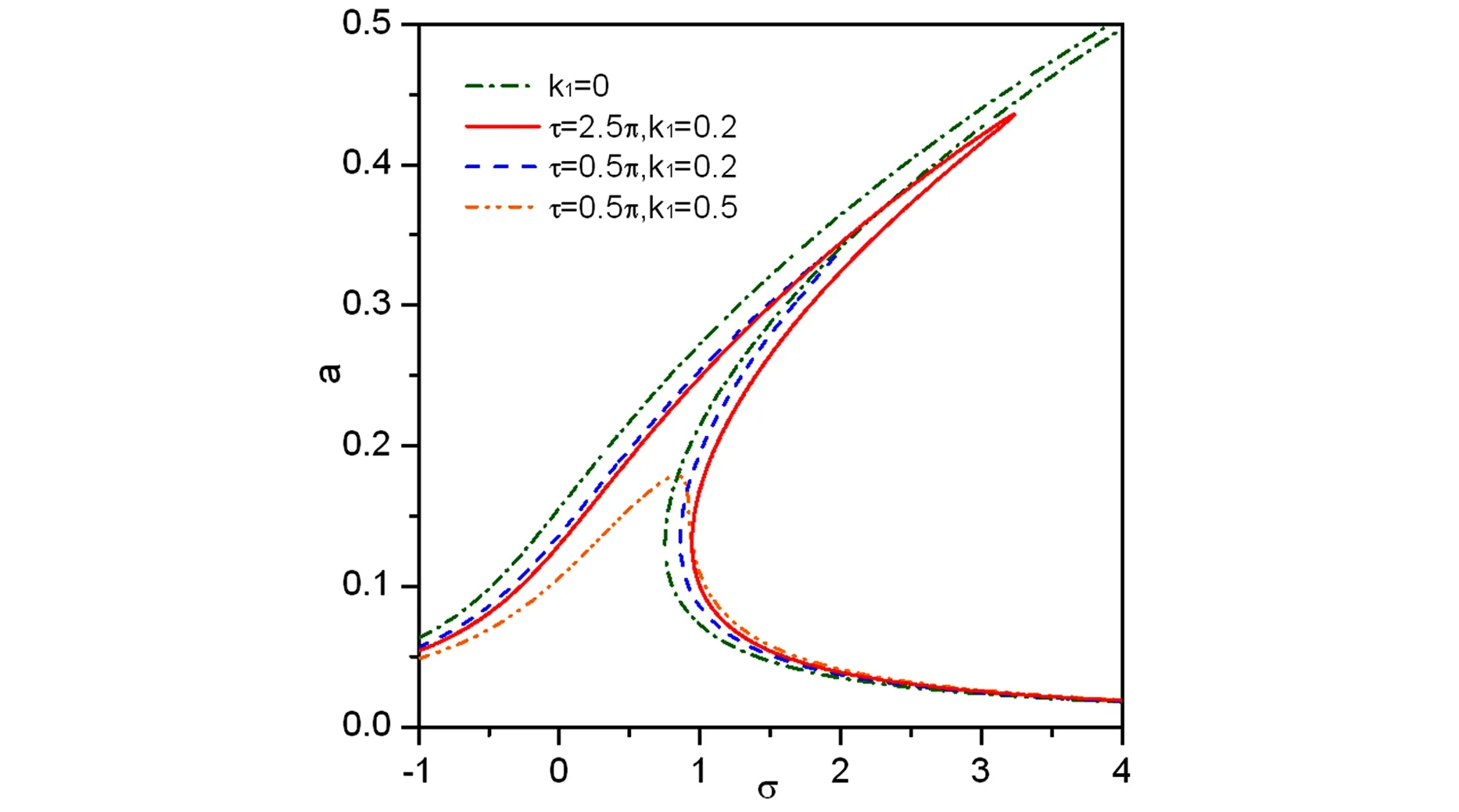
图2　时滞值和控制增益对幅频曲线的影响Fig. 2　Influence of time-delay value and control gain on the amplitude-frequency curves

选定参数f1=0.2,f2=0.03,f3=0.1,w=0.7,μ1=0.02,α1=0.1,α2=0.3.图2给出了无控和有控,不同控制增益,不同时滞值时的幅频响应曲线.从中可以看出,施加控制之后,响应幅值得到明显抑制,且当控制增益固定,随着时滞值的增大,控制效果降低.同时,当固定时滞值时,控制效果随控制增益的增大而增强.并且所有曲线呈硬弹簧特性,有多值区域.

图3　非线性系数和时滞对幅频曲线的影响Fig. 3　Effect of non-linear coefficient and time delay on amplitude-frequency curves

图3中,固定时滞值k1=0.2,得到不同非线性参数α1的幅频曲线.随着α1的增大,响应由硬弹簧特性转为软弹簧特性,非线性特征发生本质改变.当α1>0时,响应峰值随时滞减小而增大,而当α1<0时,响应峰值随时滞增大而减小.

图4　τ=π/2时,受控梁的时程曲线和相图Fig. 4　Time history curve and phase diagram of a controlled beam when τ=π/2

图5　τ=3π/4时,受控梁的时程曲线和相图Fig. 5　Time history curve and phase diagram of a controlled beam when τ=3π/4

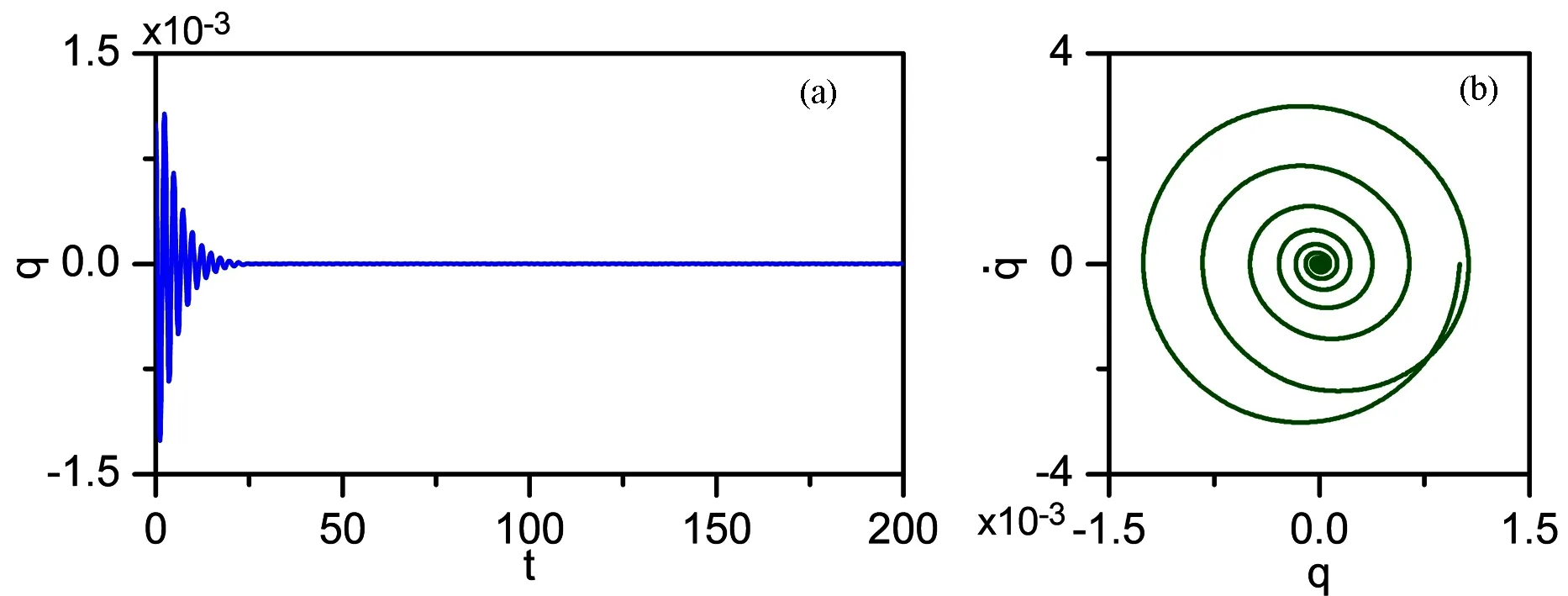
图6　τ=π时,受控梁的时程曲线和相图Fig. 6　Time history curve and phase diagram of a controlled beam when τ=π

图4～图6给出了当参数激励频率Ω≈2ω0情况下系统响应的时程曲线和相图.从图中可以看出,随着时滞值的增大,由0.5π增大到π,系统从稳定运动到拟周期运动,且响应幅值显著增大.

4　小结

本文主要研究了采用时滞位移反馈控制铰支柔性梁的主参数共振问题.利用多尺度法研究了主参数响应,得到结论如下:铰支柔性梁的非线性动力系统,主参数振动响应存在多值和跳跃现象;采用时滞位移反馈控制策略,主参数响应幅值得到明显抑制;适当的调整时滞值和控制增益,可以达到最佳控制效果.

1Hegazy U H. Single-mode response and control of a hinged-hinged flexible beam.ArchiveofAppliedMechanics, 2009,79(4):335～345

2冯志宏,霍睿.压电耦合悬臂梁的时滞反馈控制及稳定性分析.振动与冲击,2011,30(6):181～184 (Feng Z H, Huo R. Time-delay feedback control and stability analysis of piezoelectric-coupling cantilever beam.JournalofVibrationandShock, 2011,30(6):181～184 (in Chinese)).

3陈龙祥,蔡国平.旋转运动柔性梁的时滞主动控制实验研究.力学学报,2008,40(10):520～527 (Chen L X, Cai G P. Experimental study on active control of a rotating flexible beam with time delay .ChineseJournalofTheoreticalandAppliedMechanics, 2008,40(10):520～527(in Chinese))

4赵艳影,徐鉴.时滞非线性动力吸振器的减振机理.力学学报,2008,40(1):98～105 (Zhao Y Y, Xu J. Mechanism analysis of delayed nonlinear vibration absorber.ChineseJournalofTheoreticalandAppliedMechanics,2008,40(1):98～105 (in Chinese))

5Daqaq M F, Alhazza K A, Arafat H N. Non-linear vibrations of cantilever beams with feedback delays.InternationalJournalofNon-LinearMechanics, 2008,43:962～978

6刘铭,徐晓峰,张春蕊.中立型时滞反馈扭转控制系统的稳定性分析. 动力学与控制学报,2015,13(6):449～453 (Liu M, Xu X F, Zhang C R. Stability analysis of delayed torsional vibration system of neutral type.JournalofDynamicsandControl, 2015,13(6):449～453 (in Chinese))

7贾雁兵,杨晓丽,孙中奎.异质性和时滞作用下神经元网络的共振动力学. 动力学与控制学报, 2014,12(1):86～91 (Jia Y B, Yang X L, Sun Z K. Impact of diversity and delays on the resonance dynamics of neuronal networks.JournalofDynamicsandControl, 2014,12(1):86～91 (in Chinese))

8王在华,胡海岩.时滞动力系统的稳定性与分岔:从理论走向应用.力学进展,2013,43(1):1～20 (Wang Z H, Hu H Y. Stability and bifurcation of delayed dynamics systems: From theory to application. 2013,43(1):1～20 (in Chinese))

9Zhang W, Wang F X, Zu J W. Local bifurcations and codimension-3 degenerate bifurcations of a quintic nonlinear beam under parametric excitation.Chaos,SolitonsandFractals,2005,24(4):977～998

10Nayfeh A H. Linear and nonlinear structure mechanics. New York: Wiley Interscience,2004

*The project supported by the National Natural Science Foundation of China (11402085), Scientific Research Foud of Hunan Provincial Education Department (14C0464) and Foudation of Excellent Doctoral Dissertation of Hunan Province (YB2015B035)

† Corresponding author E-mail: pengjian@hnu.edu.cn

30 December 2015,revised 18 January 2016.

TIME-DELAYED FEEDBACK CONTROL OF A HINGED-HINGED FLEXIBLE BEAMUNDER PARAMETRIC EXCITATION*

Peng Jian†Zhang GaiLi Luxin

(SchoolofCivilEngineering,HunanUniversityofScienceandTechnology,Xiangtan411201,China)

The time-delayed feedback control of a hinged-hinged flexible beam under parametric excitation are investigated in this paper. Based on multiple scales method, the nonlinear principal parametric resonance of a hinged-hinged flexible beam with time-delayed state feedback are obtained. The influences of the time delay, the feedback control gain and the nonlinear coefficient on the nonlinear main parametric vibration response of the system are investigated. Moreover, the variation of the main parametric response with the control system parameters is obtained. The results show that with the increase with the feedback gain, the system response amplitude is significantly suppressed. Therefore, through selecting appropriate control system parameters, the efficiency of vibration control can be improved.

time-delay feedback,primary parametric resonance,flexible beam,vibration control,stability

E-mail: pengjian@hnu.edu.cn

10.6052/1672-6553-2016-10

2015-12-30收到第1稿,2016-01-18收到修改稿.

*国家自然科学基金(11402085),湖南省教育厅资助项目(14C0464)和湖南省优秀博士论文资助项目(YB2015B035)