一类分数阶复杂网络混沌系统的投影同步*
毛北行 李庆宾
(郑州航空工业管理学院理学院, 郑州 450015)
一类分数阶复杂网络混沌系统的投影同步*
毛北行†李庆宾
(郑州航空工业管理学院理学院, 郑州450015)
根据分数阶系统的相关理论研究了一类分数阶复杂网络混沌系统的投影同步问题,给出了分数阶复杂网络以及分数阶时滞复杂网络系统实现投影同步的充分性条件,仿真结果表明了方法的正确性.
投影同步,分数阶系统,复杂网络
引言
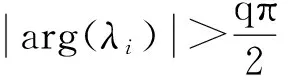
定义1[14]:Caputo分数阶导数定义为:

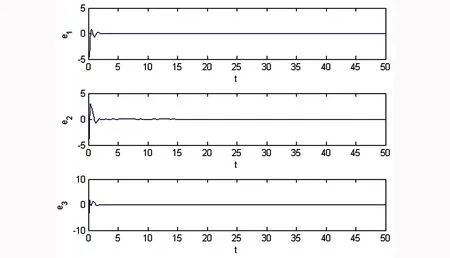
n-1<α 考虑如下一类分数阶复杂网络系统: ui(t)(i=1,2,…,N), (1) A为适当维数的常数矩阵,ui为控制输入,Γ是网络的内部耦合矩阵,C=(cij)N×N是外部耦合矩阵,满足cij=0,(i≠j),cij≥0(i≠j),对角线元素定义为: (2) 假设1:复杂网络的孤立节点的解满足: Dtqs(t)=As(t)+f(s(t)) (3) s(t)可以是一个稳定点,或者周期解,也可以是混沌轨迹. 定义1: 对给定的分数阶系统(1),若存在一个非零矩阵Λ,使得 假设2:非线性函数满足条件: ‖f(xi(t))-Λf(s(t))‖≤li‖xi(t)-Λs(t)‖,其中li为大于零的常数. 定义系统误差为: ei(t)=xi(t)-Λs(t), (i=1,2,…,N), 则有: Dtqei(t)=Aei(t)+f(xi(t))-Λf(s(t))+ 引理1[15]:对于一般的分数阶自治非线性微分方程Dtαx(t)=f(x(t)),当系统的阶数0<α≤1时,如果存在实对称正定矩阵P,使得J(x(t))=xT(t)PDtαx(t)<0,则上述分数阶系统渐近稳定. 定理1:设计控制器ui(t)=-kiei(t),若满足条件(A+(li-ki)IN)+C⊗Γ<0则分数阶复杂网络系统(1)可以实现投影同步. 证明:由 Dtqei(t)=Aei(t)+f(xi(t))-Λf(s(t))+ C⊗Γ]ei(t)<0, 根据引理1,很容易得到定理1. 考虑如下一类分数阶时滞复杂网络系统: Dtqxi(t)=Axi(t)+f(xi(t-τ))+ (i=1,2,…,N), (5) A为适当维数的常数矩阵,ui为控制输入,τ为时滞常数,Γ是网络的内部耦合矩阵,C=(cij)N×N是外部耦合矩阵,满足cij≥0(i≠j),同时对角线元素定义为: (6) 假设3:复杂网络的孤立节点的解满足: Dtqs(t)=As(t)+f(s(t-τ)) (7) s(t)可以是一个稳定点,或者周期解,也可以是混沌轨迹. 假设4:非线性函数满足条件: ‖f(xi(t-τ))-Λf(s(t-τ))‖≤ li‖xi(t-τ)-Λs(t-τ)‖ 定义系统误差为: ei(t)=xi(t)-Λs(t),(i=1,2,…,N), 则有: Dtqei(t)=Aei(t)+f(xi(t-τ))-Λf(s(t-τ))+ (8) 引理2[16]:分数阶时滞系统 Dtαx(t)=f(x(t),x(t-τ)),如果有正定的矩阵P和半正定矩阵Q满足 xT(t)PDtαx(t)+xTQx(t)- xT(t-τ)Qx(t-τ)≤0, 则上述分数阶时滞系统是Lyapunov稳定的. 定理2:设计控制器ui(t)=-kiei(t),若满足如下矩阵不等式(9),则分数阶复杂网络系统(5)可以实现投影同步. (9) 证明:根据引理2: 其中 e(t-τ)=[‖e1(t-τ)‖,‖e2(t-τ)‖,…, ‖eN(t-τ)‖]T. 选取分数阶Lorenz系统为例,系统描述为 Dtqx1=a(x2-x1) Dtqx2=bx1-x1x3-x2 Dtqx3=x1x2-cx3, Dtqs1=a(s2-s1) Dtqs2=bs1-s1s3-s2 Dtqs3=s1s2-cs3 其中x1,x2,x3为状态变量,a,b,c为系统参数,当q=0.93,a=10,b=28,c=8/3时系统处于混沌状态.为了方便,取含三个节点的网络进行仿真. 图1 定理1中的系统误差曲线Fig. 1 The system errors for Theorem 1 图2 定理2中的系统误差曲线Fig. 2 The system errors for Theorem 2 定理1中选取控制器ui(t)=-kiei(t),Λ=diag(-1,1,1),Γ=I3,li=1.2ki=1,从系统的误差曲线如图1所示, 定理2中选取控制器ui(t)=-kiei(t), Λ=diag(-1,1,1),Γ=I3,τ=0.5,li=1.5,ki=1.5,系统的误差曲线如图2所示. 研究了一类分数阶复杂网络混沌系统及其时滞系统的投影同步问题,基于Lyapunov稳定性理论和分数阶微积分的相关理论,给出了分数阶复杂网络以及分数阶时滞复杂网络实现投影同步的充分性条件,将系统实现投影同步的充分性条件转化为矩阵不等式,从而更容易MATLAB求解,仿真结果表明了方法的正确性. 1徐争辉,刘友金,谭文等.一个对称分数阶经济系统混沌特性分析.系统工程理论与实践,2014,34(5):1237~1242 (Xu Z H, Liu Y J,Tan W,et al. Chaotic dynamics in a commensurate fractional-order nonlinear economic system.SystemsEngineeringandThroryPractice,2014,34(5):1237~1242 (in Chinese)) 2郝建红,宾虹,姜苏娜等.分数阶线性系统稳定理论在混沌同步中的简单应用.河北师范大学学报自然版,2014,38(5):469~475 (Hao J H,Bin H,Jiang S N,et al. Stability theorem for fractional linear systems and its application in chaos synchronization.JournalofHebeiNormalUniversity(NaturalScuenceEdition),2014,38(5):469~475 (in Chinese)) 3钟启龙,邵永辉,郑永爱.基于TS模型的分数阶混沌系统同步.扬州大学学报(自然版),2012,17(2):46~49 ( Zhong Q L,Shao Y H,Zheng Y A. Synchronization of the fractional order chaotic systems based on TS models.JournalofYangzhouUniversity(NaturalScienceEdition),2012,17(2):46~49 (in Chinese)) 4张云雷,吴超然.基于反馈控制的分数阶时滞神经网络的同步.重庆工商大学学报(自然版),2014,31(12):49~53(Zhang Y L ,Wu C R. Synchronization of fractional -order neural network with delay based on feedback control.JournalofChongqingTechnolBusinessUniversity(NaturalScienceEdition), 2014,31(12):49~53 (in Chinese)) 5韩敏,张雅美,张檬.具有双重时滞的时变耦合复杂网络的牵制外同步.物理学报,2015,64(7):5061~5069 (Han M,Zhang Y M,Zhang M. Outer syncronization analysis of two time-varying networks with double delays based on pinning control.ActaPhysicaSinica, 2015,64(7):5061~5069 (in Chinese)) 6Lü L, Li G,Guo Y. Generalized chaos synchronization of a weighted complex network with different nodes.ChinesePhysicsB,2010,19(8):5071~5077 7Mei J, Jiang M H, Wang J. Finite-time structure identification and synchronization of drive-response systems with uncertain parameter.CommunicationsinNonlinearScienceandNumericalSimulation,2013,(18):999~1015 8余明哲,张友安.一类不确定分数阶混沌系统的滑模自适应同步.北京航空航天大学学报,2014,40(9):1276~1280 (Yu M Z, Zhang Y A. Sliding mode adaptive synchronization for a class of fractional-order chaotic systems with uncertainties.JournalofBeijingUniversityofAeronauticsandAstronautics, 2014,40(9):1276~1280 (in Chinese)) 9严胜利,张昭晗.一类不确定分数阶混沌系统的同步控制.系统仿真技术,2013,9(4):366~370 (Yan S L,Zhang Z H. Synchronization control of a class of uncertain fractional order chaotic systems.SystemSimulationTechnology, 2013,9(4):366~370 (in Chinese)) 10潘广,魏静.一种分数阶混沌系统同步的只适应滑模控制器设计.物理学报,2015,64(4):5051~5057 (Pan G,Wei J. Design of an adaptive sliding mode controller for synchronization of fractional-order chaotic systems.ActaPhysicaSinica,2015,64(4):5051~5057 (in Chinese)) 11张燕兰.分数阶Rayleigh-Duffing-like系统的自适应追踪广义投影同步.动力学与控制学报,2014,12(4):348~352 (Zhang Y L. Adaptive tracking generalized projective synchronization of fractional Rayleigh-Duffing-like system.JournalofDynamicsandControl,2014,12(4):348~352 (in Chinese)) 12董俊,张广军,姚宏,王珏,许根.分数阶异结构超混沌系统完全同步与反相同步控制.动力学与控制报,2014,12(2):119~126 (D J, Z G J, Yao H, Wang J, Xu G. The control of complete synchronization and anti-phase synchronization for fractional-order hyper-chaotic systems of different structures.JournalofDynamicsandControl,2014,12(2):119~126 (in Chinese)) 13杨丽新,江俊.分数阶复杂网络系统的混合投影同步研究.动力学与控制学报,2015,13(1):52~55 (Yang L X,Jiang J. Hybrid projective synchronization of fractional-order complex dynamical networks.JournalofDynamicsandControl,2015,13(1):52~55 (in Chinese)) 14Podlubny. Fractional differential equation. Academic Press:San Diego,CA ,USA,1999 15胡建兵,赵灵冬.分数阶系统稳定性理论与控制研究.物理学报,2013,62(24):5041~5047 (Hu J B, Zhao L D. Stability theorem and control of fractional systems.ActaPhysicaSinica,2013,62(24):5041~5047 (in Chinese)) 16赵灵冬.分数阶非线性时滞系统的稳定性理论及控制研究[博士学位论文].上海:东华大学,2014 (Zhao L D. The stability theory of fracional nonlinear tiem-delay systems and its control[PhD Thesis]. Shanghai:Donghua University,2014 (in Chinese)) *The project supported by the National Natural Science Foundation of Tianyuan (11226337) † Corresponding author E-mail: bxmao329@163.com 18 May 2015,revised 18 September 2015. PROJECTIVE SYNCHRONIZATION OF A CLASS OF FRACTIONAL-ORDER COMPLEX NETWORK CHAOS SYSTEMS* Mao Beixing†Li Qingbin (DepartmentofMathematicsandPhysics,ZhengzhouInstituteofAeronauticalIndustryManagement,Zhengzhou450015,China) The paper studied the projective synchronization problem of a class of fractional-order complex network chaos systems based on fractional order systems theory. The sufficient conditions for fractional-order complex network and its time-delayed systems to realize the projective synchronization was proposed. Numerical simulations of chaotic system verified the validity of the proposed method. projective synchronization,fractional order systems,complex networks E-mail: bxmao329@163.com 10.6052/1672-6553-2015-72 2015-05-18收到第1稿,2015-09-18收到修改稿. *国家自然科学基金数学天元基金资助项目(11226337)1 分数阶复杂网络系统的投影同步
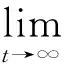
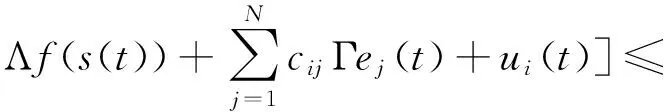
2 分数阶时滞复杂网络系统的投影同步


3 数值仿真


4 结论

