两个耦合Van der Pol振子系统的一阶近似守恒量*

楼智美

(绍兴文理学院物理系, 绍兴　312000)



两个耦合Van der Pol振子系统的一阶近似守恒量*

楼智美†

(绍兴文理学院物理系, 绍兴312000)

用直接积分法计算两个耦合Van der Pol振子系统的一阶近似守恒量,将两个耦合Van der Pol振子系统看成是未受微扰系统与微扰项的迭加,先通过坐标变换将未受微扰系统解耦,并对解耦系统的3种可能状态进行讨论,得到未受微扰系统的13个精确守恒量,再考虑微扰项对精确守恒量的影响,运用一阶近似守恒量的性质,得到1个稳定的一阶近似守恒量.另外,由13个精确守恒量直接得到13个平凡的一阶近似守恒量.

Van der Pol振子系统,精确守恒量,一阶近似守恒量

引言

许多实际力学系统的运动微分方程中常常含非线性微扰项,由于微扰项的存在,使力学系统的对称性遭到破损,一些精确守恒量的形式发生变化或消失,精确解不再成立,稳定性受到影响.因此,研究实际力学系统的近似守恒量对于研究其力学特性至关重要[1-13].目前关于微分方程近似守恒量的研究主要采用近似Lie对称性理论[1]、近似Noether对称性理论[2]和直接积分法[3].引进近似的群无限小变换,微分方程在此变换下近似保持不变则为近似Lie对称性；哈密顿作用量在此变换下近似保持不变则为近似Noether对称性,所得的守恒量为近似守恒量；直接积分法是从近似守恒量的性质出发,把受微扰系统视为未受微扰系统与微扰项的迭加,先选择合适的方法求得未受微扰系统的精确守恒量,再考虑微扰项对精确守恒量的影响,最后利用近似守恒量的性质求得守恒量.用近似对称性理论求近似守恒量要用到Lagrange函数和近似的群无限小变换,并需解出近似的无限小生成元、规范函数,计算较繁复,理论性强又比较抽象.用直接积分法求近似守恒量,思想方法简单,物理意义明确,计算方法灵活.

两个耦合Van der Pol振子系统是一实际的力学系统[4],已广泛应用于非线性动力学和数学物理的研究中.本文采用直接积分法计算两个耦合Van der Pol振子系统的一阶近似守恒量,先通过坐标变换对未受微扰系统进行解耦,并对解耦系统的3种可能状态进行讨论,直接得到未受微扰系统在新坐标系下的13个精确守恒量,利用坐标反变换得到未受微扰系统在原坐标系下的13个精确守恒量,再考虑微扰项对精确守恒量的影响,运用一阶近似守恒量的性质,得到1个稳定的一阶近似守恒量.另外,根据一阶近似守恒量的性质,由13个精确守恒量直接得到13个平凡的一阶近似守恒量.

1　未受微扰作用系统的精确守恒量

两个耦合Van der Pol振子系统的运动微分方程可以表示成[4]

(1a)

(1b)

其中0<ε≪1,为微扰系数.A,B为线性耦合系数,且为不为0的实常数.

系统(1)可以改写成

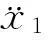
=g1(ε0)+εg1(ε1)

(2a)

=g2(ε0)+εg2(ε1)

(2b)

与系统(2)相应的未受微扰作用系统的运动微分方程可表示成

(3a)

(3b)

系统(2)可以看成是系统(3)与微扰项εg1(ε1)、εg2(ε1)的迭加, 系统(3)是两个线性耦合的振子系统.引进坐标变换

u1=x1+x2,u2=x1-x2

(4)

对系统(3)解耦后得

(5a)

(5b)

在新坐标系下,系统(5)不再相互耦合,可以方便地求得系统(5)在新坐标系下的精确守恒量, 再利用坐标反变换可求得系统(5)在原坐标系下的精确守恒量.

(5a)式表示谐振子的运动微分方程,在A、B任意取值下,(5a)式存在两个基本的精确守恒量[14]

(6a)

(6b)

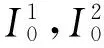
(7)

(5b)式表示线性阻尼振子的运动微分方程,其精确守恒量与A、B的取值有关.(5b)式的解存在如下三种可能状态,在不同的状态下,其中一些精确守恒量的表达式也不同.

1)B2>1+2A,为过阻尼状态,(5b)式存在两个基本的精确守恒量

(8a)

(8b)

(9a)

(9b)

2)B2<1+2A, 为欠阻尼状态, (5b)式存在两个基本的精确守恒量[15]

=[ω(x1-x2)sin(ωt)+

(10a)

=[ω(x1-x2)cos(ωt)-

(10b)

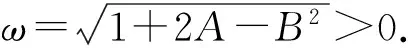
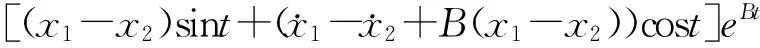
(11a)

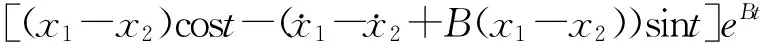
(11b)

3)B2=1+2A, 为临界阻尼状态, (5b)式存在一个基本的精确守恒量

(12)

在上述三种可能状态下,可以统一构建一个具有能量量纲的精确守恒量

(1+2A)(x1-x2)2]e2Bt

(13)

2　耦合Van der Pol 振子系统的一阶近似守恒量

设耦合Van der Pol振子系统(2)的一阶近似守恒量可表示成[5]

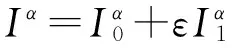
(14)

一阶近似守恒量的性质为[5]

(15)

将(14)式代入(15)式并展开,令ε0,ε1的系数分别等于0,忽略ε2以上项,可得

(16a)

(16b)

(17a)

(17b)

(17c)

(17d)

(17e)

(17f)

(17g)

(17h)

(17i)

(17j)

(17k)

(17l)

(17m)

(18)

则系统存在1个稳定的一阶近似守恒量

(19)

(20)

3　结论

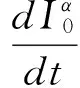
1Leach P G L, Moyo S, Cotsakis S, Lemmer R L. Symmetry, singularities and integrability in complex dynamics Ⅲ: approximate symmetries and invariants.JournalofNonlinearMathematicalPhysics, 2001,8(1):139～156

2Govinder K S, Heil T G, Uzer T. Approximate Noether symmetries.PhysicsLettersA, 1998,240(3):127～131

3楼智美. 含非线性微扰项的二阶动力学系统的一阶近似守恒量的一种新求法. 物理学报, 2014,63(6):060202 (Lou Z M. A new method to obtain first order approximate conserved quantities of second-ordinary dynamics system containing nonlinear perturbation terms.ActaPhysicaSinica, 2014,63(6):060202 (in Chinese))

4Naeem I, Mahomed F M. Approximate first integrals for a system of two coupled van der Pol oscillators with linear diffusive coupling.MathematicalandComputationalApplications, 2010,15(4):720～731

5Unal G. Approximate generalized symmetries, normal forms and approximate first integrals.PhysicsLettersA, 2000,266(2):106～122

6Dolapci I T, Pakdemirli M. Approximate symmetries of creeping flow equations of a second grade fluid.InternationalJournalofNon-linearMechanics, 2004,39(10):1603～1619

7Kara A H, Mahomed F M, Qadir A. Approximate symmetries and conservation laws of the geodesic equations for the Schwarzschild metric.NonlinearDynamics, 2008,51(1-2):183～188

8Grebenev V N, Oberlack M. Approximate Lie symmetries of the Navier-Stokes equations.JournalofNon-linearMathematicalPhysics, 2007,14(2):157～163

9Johnpillai A G,Kara A H, Mahomed F M. Approximate Noether-typesymmetries and conservation laws via partial Lagrangians for PDEs with a small parameter.JournalofComputationalandAppliedMathematics, 2009, 223(1):508～518

10楼智美. 微扰Kepler系统轨道微分方程的近似Lie对称性与近似不变量. 物理学报, 2010,59(10):6764～6769 (Lou Z M. Approximate Lie symmetries and approximate invariants of the orbit differential equation for perturbed Kepler system.ActaPhysicaSinica, 2010,59(10):6764～6769 (in Chinese))

11楼智美,梅凤翔,陈子栋. 弱非线性耦合二维各向异性谐振子的一阶近似Lie对称性与近似守恒量. 物理学报, 2012,61(11):110204 (Lou Z M, Mei F X, Chen Z D. The first-order approximate Lie symmetries and approximate conserved quantities of the weak nonlinear coupled two-dimensional anisotropic harmonic oscillator.ActaPhysicaSinica2012,61(11):110204 (in Chinese))

12Zhang Z Y, Yong X L, Chen Y F. A new method to obtain approximate symmetry of nonlinear evolution equation form perturbations.ChinesePhysicsB, 2009,18(7):2629～2633

13楼智美. 两自由度微扰力学系统的二阶近似守恒量. 动力学与控制学报, 2015,13(3):165～169 (Lou Z M. Second order approximate conserved quantities of two dimensional perturbed mechanics system.JournalofDynamicsandControl, 2015,13(3):165～169 (in Chinese))

14丁光涛. 关于谐振子第一积分的研究. 物理学报, 2013,62(6):064502 (Ding G T. A study on the first integrals of harmonic oscillators.ActaPhysicaSinica, 2013,62(6):064502 (in Chinese))

15丁光涛. 关于线性阻尼振动第一积分的研究. 物理学报, 2013,62(6):064501 (Ding G T. On the first integrals of linear damped oscillators.ActaPhysicaSinica, 2013,62(6):064501 (in Chinese))

*The project supported by the National Natural Science Foundation of China(11472177)

† Corresponding author E-mail: louzhimei@usx.edu.cn

16 April 2015,revised 02 July 2015.

FIRST ORDER APPROXIMATE CONSERVED QUANTITIES OF TWO COUPLED VAN DER POL OSCILLATORS SYSTEM*

Lou Zhimei†

(DepartmentofPhysics,ShaoxingUniversity,Shaoxing312000,China)

The first order approximate conserved quantities of two coupled Van der Pol oscillators system is investigated by using direct integral method. Two coupled Van der Pol oscillators system is taken as the combination of unperturbed system and perturbed terms. Firstly, the unperturbed system is decoupled by transforming coordinates, and thirteen exact conserved quantities of unperturbed system are obtain by discussing the three possible condition of uncoupled system. Second, the influence of perturbed terms on exact conserved quantities is examined. Finally, a stable first order approximate conserved quantity of the system is developed according to the characteristic of the first order approximate conserved quantities. In additional, thirteen trivial conserved quantities from thirteen exact conserved quantities are also received.

Van der Pol oscillators systems,exact conserved quantities,first order approximate conserved quantities

E-mail: louzhimei@usx.edu.cn

10.6052/1672-6553-2015-58

2015-04-16收到第1稿,2015-07-02收到修改稿.

* 国家自然科学基金资助项目(11472177)