基于时滞思想的一类非线性弹性杆结构动力行为的研究*
牛丽芳 张建文 段周波
(太原理工大学数学学院, 太原 030024)
基于时滞思想的一类非线性弹性杆结构动力行为的研究*
牛丽芳†张建文段周波
(太原理工大学数学学院, 太原030024)
基于时滞思想,利用改进的Galerkin方法,研究了一类非线性弹性杆方程的长时间行为.该方法将控制方程的解投影到由其线性算子的特征函数所张成的完备空间内,并截取有限阶模态来逼近真实解,从而将无穷维动力系统近似为有限维动力系统.根据时滞思想,构造了反映高、低阶模态关系的时滞表达式,使得在数值模拟过程中无需通过复杂数值积分即可直接获取高阶位移分量,从而降低了系统维数,缩减了计算量.对系统进行了数值模拟及分析,得到用较低的模态可描述系统解的最终状态.
时滞惯性流形,非线性Galerkin方法,非线性弹性杆
引言
设无穷维动力系统
(1)
其中A在某一Hilbert空间V上是线性、自共轭无界算子,R是非线性算子.对给定的n∈N,Vn⊂V是n维子空间,记Pn是从V到Vn的L2_正交投影算子,并记Qn=I-Pn.记p=Pnu,q=Qnu,故u=p+q. 把Pn和Qn应用到方程(1),则产生了一系列如下形式的方程
(2)
(3)
事实上,传统的Galerkin方法相当于在(2)中令q=0而得到的一系列有限维的动力方程.

处于这样的考虑,大家认为对大多数微分动力系统来说,一般依赖于系统的过去.为此,A Debussche和R Temam[4]提出了时滞惯性流形的概念,它说明大小涡分量间的相互关系不是一种简单的瞬时作用,而是与涡的发展历史相关,即改变了惯性流形和近似惯性流形方法中高、低阶分量间相互作用为瞬时行为的隐合假定,而认为这种作用与系统的发展历史相关的,即
q=φ(p(t),q(t-T))
(T是一个适当的时间延迟)
(4)
这种形式的IMD对大漩涡方程的最小维数几乎没有限制,而且可以实现对非线Galerkin方法进行改进,在减弱其可行性条件的同时,能够保持其良好的稳定性和收敛性.由于时滞惯性流形是一类有限维光滑流形,而且在一定的时间内,方程的解轨道都会进入到它的一个小邻域里,因此研究无穷维动力系统长时间形态具有非常重要的意义.另外,时滞惯性流形的存在性不需要微分方程具备严格的谱间隙条件,因此可以在更广泛的耗散方程[5-7]中应用.
从时滞惯性流形角度,关于杆、梁、板结构的研究到目前还很少.本文试图根据时滞惯性流形思想,来研究如下非线性黏弹性杆方程
utt-Δu-rΔut-βΔutt-φ(0)Δu-
(5)
其中方程具有齐次边界条件
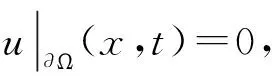
(6)
和初始条件
u(x,t)=u0(x),x∈Ω,t≤0
(7)
且Ω是R3的一个有界开集,并具有光滑边界∂Ω,r,β>0是非负常数,φ(0),φ(∞)>0,φ′(s)<0(∀s∈R+),f满足临界增长指数条件.2014年,牛丽芳和张建文[8]研究了上述非线性演化方程的稳定性,证明了给系统整体解存在全局吸引子.
本文在上述基础上,利用时滞惯性流形思想,提出一种新的非线性Galerkin方法,对系统(5)~(7)进行数值模拟.具体方法是,把原始方程的解投影到由控制方程中线性算子的特征函数所张成的完备空间内,并构造出无限维子空间内的动力行为与有限维子空间内的动力行为之间的耦合作用,该耦合作用认为高低阶分量间的相互作用并不是一种简单的瞬时行为,而是与模态发展的历史有关.这种方法是将高阶模态用低阶模态来表示,并引入时间滞后,即保留了计算精度,还减少了关于时间的非线性耗散的二阶自治系统的自由度,降低求解规模对计算机资源的要求.
1 预备知识
下面给出本章所需要的一些定义和假设条件.

在对系统(5)~(7)整体弱解的研究中[8],对非线性项f∈C0(R,R)作如下假设:

(H2)存在常数k0,使得

当n=1,2∀s∈R;
其中k0是正常数.

其中λ1是-Δ在Dirichlet边界条件下的第一特征值.
f(s)s≤λs2+k1, ∀s∈R,
(8)
和

(9)
其中λ<λ1.
为了方便,记μ(s)=-φ′(s)和φ(∞)=α,其中α是一个正常数.记忆核μ满足如下假设:
(H3)μ∈C1(R+)∩L1(R+),μ(s)≥0,
μ′(s)≤0∀s∈R+;

(H5)μ′(s)+dμ(s)≤0, ∀s∈R+,其中常数d>0.
最后,引入Hilbert空间.
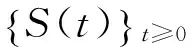
2 基于时滞惯性流形思想的算法
在上一节中,系统(5)~(7)的整体解在一定条件下存在全局吸引子,即解是稳定的.因此,从理论上保证了对系统(5)~(7)进行Galerkin截断的合理性.
接下来,将利用时滞惯性流形思想对系统(5)~(7)进行Galerkin截断、数值模拟及分析,为了方便,需要对系统中抽象的函数取为具体函数.
在系统(5)~(7)中取Ω=(0,1),N=1,φ(s)=1+e-2s,f(u)=0,有φ(∞)=1,φ(0)=2,则系统(1)~(3)式化为
(10)
记μ(s)=-φ′(s),下面验证取定的这些非线性项满足本章的假设条件(H1)~(H5):
(H1)μ(s)=2e-2s,
显然μ(s)∈C1(R+)∩L1(R+),μ(s)≥0,μ′(s)≤0∀s∈R+;

(H3)μ′(s)+μ(s)=-4e-2s+2e-2s≤0,∀s∈R+
(H4)存在常数k3=1>0,使得f′(v)=0≤k3, ∀v∈R;

(11)
将(11)代入(10)中,得
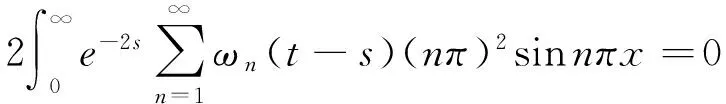
(12)
用(12)与sinmπx在Ω上作L2(Ω)中内积,得到系统离散化的方程组

(13)
其中m=1,2,….
基于时滞惯性流形思想,降低系统维数,减少计算时间.截取方程组(13)的前2N阶模态,设前N阶模态为低阶的模态,后N阶模态为高阶模态,将时间区间[0,T]分为t0,t1,t2,…,ti,…,步长为k,ωj(ti)对应于ti时刻j阶模态的值.
ti时刻前N阶模态可表示为:

sinmπxdx=A
m=1,2,…,N
(14)

(15)
(16)
得到ti时刻后N阶模态为:

m=N+1,N+2,…,2N
(17)
具体的IMD算法为:
ti时刻,前N阶模态表示为(i=0,1,2,…,s;m=1,2,…,N):
(18)
后N阶模态中,t0,t1时刻表示为(i=0,1,m=N+1,N+2,…,2N):
(19)
后N阶模态中,ti时刻表示为(i=2,…,s;m=N+1,N+2,…,2N):
(20)
IMD算法通过构造了含有时滞的高、低阶模态的相互关系,使得在数值模拟过程中无需通过复杂数值积分,即可直接获得高阶位移分量.
3 数值分析
下面利用上面所得到的时滞惯性流形算法对系统(5)~(7)进行数值模拟及分析,其中所有的图都是描绘弹性杆的中心位置.
在相同参数下,分别取前40阶模态、600阶模态、1000阶模态和2000阶模态,得到图1、图2、图3和图4.分析这四个图,看到在相同初始速度下,系统最终状态是一样的.也就是说,利用本节的算法,取前40阶模态,就可准确描述系统(5)~(7)解的最终状态.
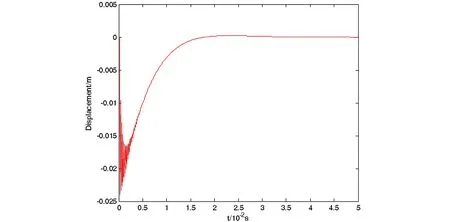
图1 取N=20,β=0.01,γ=2.0,初始速度为-12m/s得到的位移-时间历程图Fig. 1 Time history of displacement when N=20,β=0.01,γ=2.0
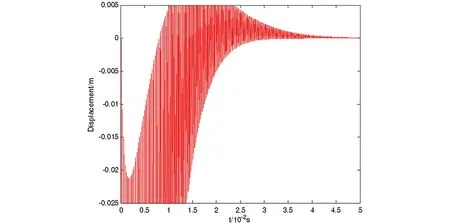
图2 取N=300,β=0.01,γ=2.0,初始速度为-12m/s得到的位移-时间历程图Fig. 2 Time history of displacement when N=300,β=0.01,γ=2.0
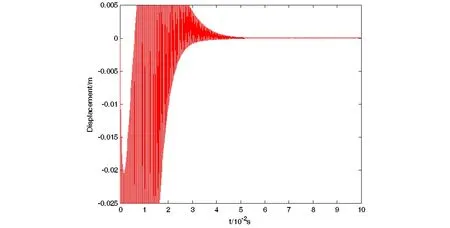
图3 取N=500,β=0.01,γ=2.0,初始速度为-12m/s得到的位移-时间历程图Fig. 3 Time history of displacement when N=500,β=0.01,γ=2.0
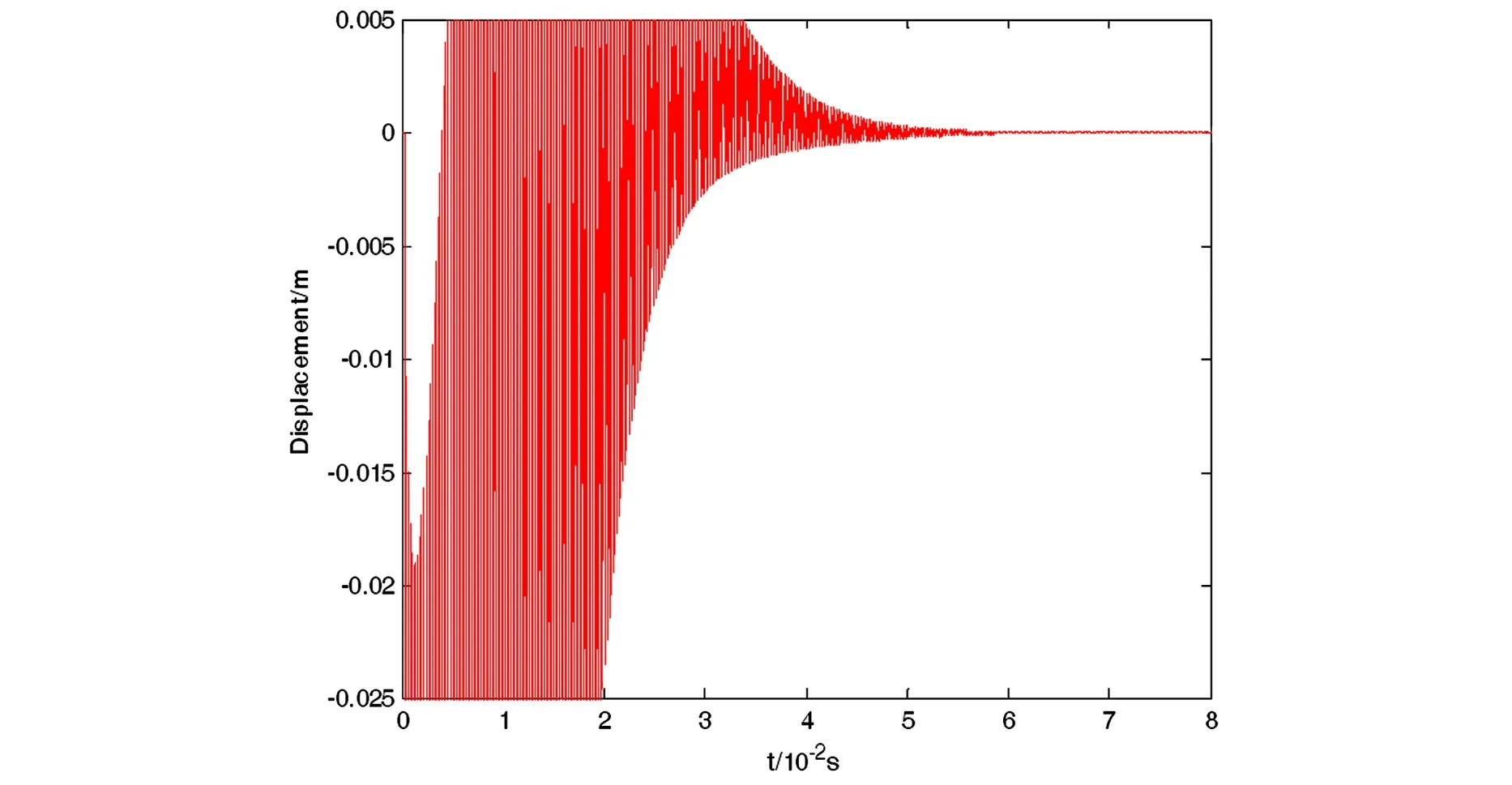
图4 取N=1000,β=0.01,γ=2.0,初始速度为-12m/s得到的位移-时间历程图Fig. 4 Time history of displacement when N=1000,β=0.01,γ=2.0
通过数值分析,在本章例子中,相比传统的Galerkin方法,IMD算法同样可用较少模态来描述系统的最终状态.除此之外,从算法上可以看到,简化了程序,大幅缩减了计算量,节约了时间,进一步降低了求解规模对计算机的要求,有一定的优越性.
1Foias C, Sell G R, Temam R. Inertial manifolds for nonlinear evolutionary equations.JournalofDifferentialEquations, 1998,73(2):309~353
2Foias C, Manley O, Temam R. On the interaction of small eddies in two-dimensional turbulence flows.MathModelingandNumericalAnalysis, 1988,22(1):93~118
3Hosoya M, Yamada Y. On some nonlinear wave equations Ⅱ: global existence and energy decay of solutions.JournaloftheFacultyofScience,UniversityofTokyo, 1991,38:239~250
4Debussche A, Temam R. Inertial Manifold with Delay.AppliedMathematicsLetters, 1995,8(2):21~24
5张家忠,陈丽莺,梅冠华等. 基于时滞惯性流形的浅拱动力屈曲研究. 振动与冲击,2009,28(6):100~103,167 (Zhang J Z,Chen L Y, Mei G H, et al. Dynamic bucking analysis of shallow parabolic arch based on the method of inertial manifolds with time delay.JournalofVibrationandShock, 2009,28(6):100~103,167 (in Chinese))
6Zhang J Z, Liu Y, Lei P F, Sun X. Dynamic snap-through buckling analysis of shallow arches under impact load based on approximate inertial manifolds.DynamicsofContinuous,DiscreteImpulsiveSystems,SeriesB(DCDIS-B), 2007,14:287~291
7Suzuki R. Asymptotic behavior of solutions of quasilinear parabolic equations with supercritical nonlinearty.JournalofDifferentialEquations, 2003,190(1):150~181
8牛丽芳,张建文,张建国. 一类带记忆项的非线性弹性杆的全局吸引子. 数学的实践与认识,2013,43(18):262~268 (Niu L F, Zhang J W, Zhang J G. Existence of global attractors for a class of nonlinear elastic rod equation with memory type.MathematicsinPracticeandTheory, 2013,43(18):262~268 (in Chinese))
*The project supported by the Natural Science Foundation for Young Scientists of Shanxi Province, China (2015021009)
† Corresponding author E-mail:niulifangfly@163.com
15 February 2015,revised 08 September 2015.
ASYPTOTIC BEHAVIOR FOR A NONLINEAR ELASTIC ROD BASED ON THE INERTIAL MANIFOLD WITH DELAY*
Niu Lifang†Zhang JianwenDuan Zhoubo
(CollegeofMathematics,TaiyuanUniversityofTechnology,Taiyuan030024,China)
In this paper, based upon a new concept of the inertial manifolds with delay, a kind of nonlinear elastic rod is studied by an improved version of the nonlinear Galerkin method. This method was employed to project the solutions of the governing equations onto the complete space spanned by the eigen-functions of equation operators. With the truncation of modes to approach the solution, the original infinite dimensional dynamic system is approximated as a finite one. Furthermore, a time-delay expression which implies the interaction between higher and lower modes was constructed. With the time-delay expression presented, the higher displacement modes were obtained directly without a complicated numerical integration, resulting in a system with less degree-of-freedoms and reducing the computation time.
inertial manifold with delay,nonlinear Galerkin method,nonlinear elastic rod
E-mail:niulifangfly@163.com
10.6052/1672-6553-2015-67
2015-02-15收到第1稿,2015-09-08收到修改稿.
*山西省青年科技研究基金资助项目(2015021009)

