广义BBM方程的无穷序列新解*

李宁　套格图桑

(内蒙古师范大学 数学科学学院， 呼和浩特　010022)



广义BBM方程的无穷序列新解*

李宁†套格图桑

(内蒙古师范大学 数学科学学院， 呼和浩特010022)

利用第二种椭圆方程的已知解与解的非线性叠加公式,构造了广义BBM方程的由Jacobi椭圆函数解、双曲函数和三角函数组成的无穷序列新解.

第二种椭圆方程,解的非线性叠加公式,无穷序列新解

引言

众所周知非线性波动问题是有许多物理背景的.非线性发展方程是研究此类物理问题的重要数学模型,而非线性发展方程的求解等相关问题是孤立子理论的重要研究内容之一.所以研究非线性发展方程的求解方法等问题具有重要的研究意义.人们为了寻找非线性发展方程的精确解,提出了许多有效的直接方法,也已取得了很多的成果[1-6].

文献[7]构造了广义BBM方程(1)的由双曲函数解、三角函数解、指数函数解和有理解构成的有限多个新精确解.本文利用第二种椭圆方程的已知解与解的非线性叠加公式,构造了广义BBM方程(1)的由Jacobi椭圆函数解、双曲函数和三角函数组成的无穷序列新解.

1　二种椭圆方程的相关结论

下面给出的第二种椭圆方程解的非线性叠加公式等结论,构造广义BBM方程(1)的无穷序列新解.

ut+αupux+βu2pux-δuxxt=0 (p>0,δ≠0)

(1)

1.1第二种椭圆方程的已知解

根据文献[7]的相关结论,我们得到第二种椭圆方程

(2)

的如下解.

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

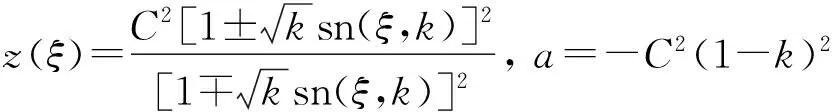
(21)

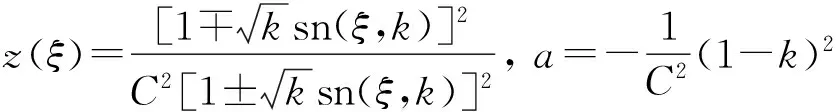
b=H,c=-C2(1-k)2

(22)

(23)

(24)

b=2(1+k2),c=B2(1-k2)2

(25)

z(ξ)=J7(ξ),a=B2(1-k2)2,

(26)

b=F,c=∓16A2kP2

(27)

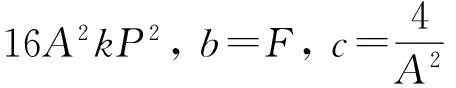
(28)

b=E,c=4Φ

(29)

(30)

(31)

z(ξ)=L2(ξ),a=∓16B2k2P2,

(32)

b=E,c=∓16A2K

(33)

z(ξ)=L3(ξ),a=∓16A2K,

(34)

(35)

(36)

b=E,c=∓16C3K

(37)

z(ξ)=L5(ξ),a=∓16C3K,

(38)

(39)

(40)

(41)

(42)

(43)

(44)

(45)

(46)

(47)

(48)

(49)

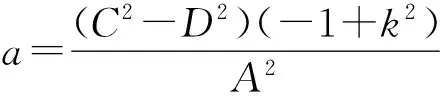
(50)

其中,J1(ξ)=C2[nd(ξ,k)±ksd(ξ,k)]2,

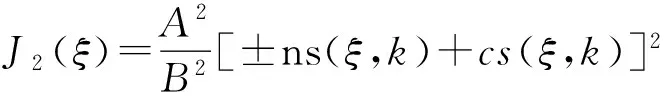
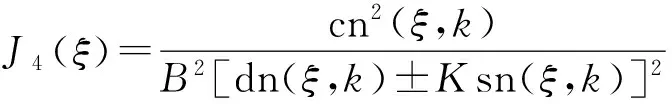
J5(ξ)=B2[dc(ξ,k)±Ksc(ξ,k)]2,

J6(ξ)=B2[dn(ξ,k)±cn(ξ,k)]2,

J7(ξ)=B2[ds(ξ,k)±cs(ξ,k)]2,

J8(ξ)=A2[ns(ξ,k)∓ksn(ξ,k)]2,

J9(ξ)=B2[kcn2(ξ,k)±(1∓k)]2,

F1(ξ)=A2[-(1∓K)sn2(ξ,k)+1]2,

F2(ξ)=B2[k2cn2(ξ,k)+Θ]2,

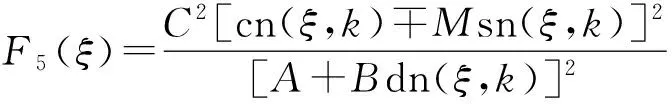
S1(ξ)=C2[dn(ξ,k)∓Nsn(ξ,k)]2,

S2(ξ)=C2[dn(ξ,k)∓Nsn(ξ,k)]2,

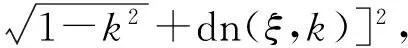
S5(ξ)=C2[∓kcn(ξ,k)+dn(ξ,k)]2,

S6(ξ)=[Dcn(ξ,k)+Cdn(ξ,k)]2,

L2(ξ)=B2[dn2(ξ,k)-P]2ns2(ξ,k),

L3(ξ)=A2[-(1∓K)sn2(ξ,k)+1]2nd2(ξ,k),

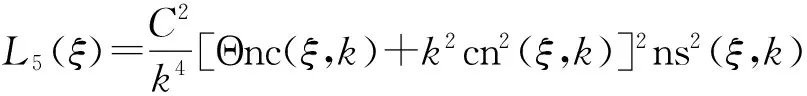
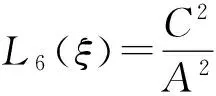
Φ=∓4B2(±2(1-k2)+(k2-2)K),P=1∓k,

E=4(2-k2∓6K),

F=4(-1±6k-k2),H=2(1+6k+k2),

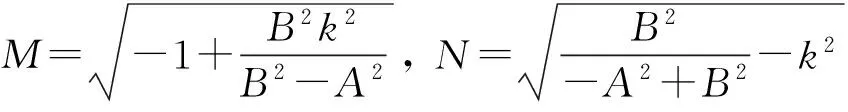
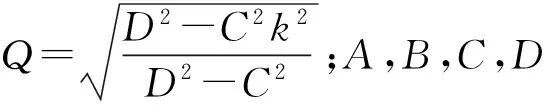
1.2第二种椭圆方程解的非线性叠加公式

若zn-1(ξ)是第二种椭圆方程(2)的非常数解,则下列zn(ξ)也是方程(2)的解.

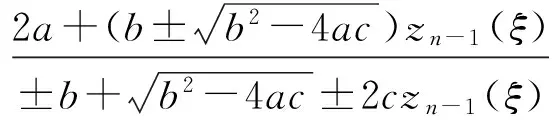
(51)

(52)

(53)

这里a,b,c是第二种椭圆方程(2)的系数.

2　广义BBM方程的无穷序列新解

对方程(1)进行行波变换u(x,t)=u(ξ),ξ=x+ωt,并对ξ积分一次后得到下列常微分方程(积分常数取为零)

δωu″(ξ)=0

(54)

假设方程(54)的形式解为如下：

(55)

将(55)式代入(54),整理后得到如下常微分方程：

(p-1)δω[v′(ξ)]2-pδωv(ξ)v″(ξ)=0

(56)

令

v(ξ)=g0z(ξ)+g1z2(ξ)

(57)

其中z(ξ)满足第二种椭圆方程(2).

将(57)和第二种椭圆方程(2)一起代入(56),并令zj(ξ)(j=0,1,2,…)的系数为零后得到一个非线性代数方程组(未列出).用符号计算系统Mathematica求出方程组的如下解:

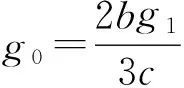
(58)

将(57)和(58)式一起代入,(55)式后得到广义BBM方程(1)的如下形式的精确解：

(59)

这里p>0,而且δ,a满足如下限制条件：

(60)

通过第二种椭圆方程(2)的已知解(3)～(50)和解的叠加公式(51)～(53),获得第二种椭圆方程(2)的无穷序列解.再将这些无穷序列解分别代入(59)式后即可获得广义BBM方程(1)的无穷序列新解.比如：通过下列叠加公式,获得由Jacobi椭圆函数解、双曲函数和三角函数组成的无穷序列新解.

(61)

当n=0时,将公式(61)的第三式代入第一式后获得如下解.

u0(x,t)=

(62)

当k=0时,Jacobi椭圆函数解(62)转化为如下三角函数解

u0(x,t)=

(63)

当k=1时,Jacobi椭圆函数解(62)转化为如下双曲函数解

u0(x,t)=

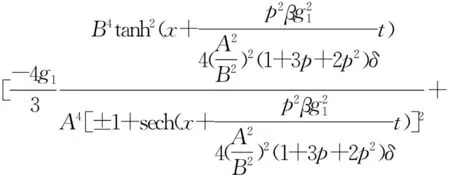
(64)

3　结论

文献[7]构造了广义BBM方程的由双曲函数解、三角函数解、指数函数解和有理解构成的有限多个新精确解.本文利用第二种椭圆方程解的非线性叠加公式等结论,构造了广义BBM方程(1)的Jacobi椭圆函数无穷序列新解.当k=0时,Jacobi椭圆函数无穷序列解,退化为三角函数解.当k=1时,Jacobi椭圆函数无穷序列解退化为双曲函数解.

1高翔,化存才. 时变系数下耦合KdV和Burgers方程组的孤波解. 动力学与控制学报,2014,12(4):295～303 (Gao X, Hua C C. Solitary wave solutions for coupled kdv-burgers equations with variable coefficients.JournalofDynamicsandControl,2014,12(4):295～303 (in Chinese))

2Sun Y Z, Wang Z L, Wang G W, Liu X Q. Soliton solutions for generalized fifth-order KdV and BBM equations with variable coefficients.ChineseJournalofQuantumElectronics, 2013,30(4):388～404

3Zhu W T,Ma S H, Fang J P, Ma Z Y, Zhu H P. Fusion, fission, and annihilation of complex waves for the (2+1)-dimensional generalized Calogero-Bogoyavlenskii-Schiff system.ChinesePhysicsB, 2013,23(6):060505(1-5)

4Taogetusang, Sirendaoerji, Li S M. New application to Riccati equation.ChinesePhysicsB, 2010,19(8):080303(1～6)

5Weiss J, Tabor M, Carnevale G. The Painleve property for partial differential equations.JournalofMathematicalPhysics,1983,24(3):522～526

6Cheng X P, Yang Y Q, Li J Y. Solitary and Periodic Waves in Coupled KdV Equations with Different Linear Dispersion Relations.CommunicationsinTheoreticalPhysics, 2014,61(1):1～6

7套格图桑. 非线性发展方程求解中辅助方程法的历史演进. 北京:中央民族大学出版社,2012: 168～174,243～247 (Taogetusang. Historical evolution of auxiliary equation method for solving nonlinear evolution equations. Beijing:The Press of the Minzu University of China, 2012:168～174,243～247 (in Chinese))

*The project supported by the Natural Science Foundation of China(11361040), Science Research Foundation of Institution of Higher Education of Inner Mongolia Autonomous Region, China(NJZY16180) and Natural Science Foundation of Inner Mongolia Autonomous Region, China(2015MS0128)

† Corresponding author E-mail: 379338089@qq.com

19 December 2014,revised 22 June 2015.

THE NEWINFINITE SEQUENCE SOLUTIONS OF THE GENERALIZED BBM EQUATION*

Li Ning†Taogetusang

(InstituteofMathematicalSciences,InnerMongolNormalUniversity,Hohhot010022,China)

Based on the known solutions of the second kind of elliptic equation and the nonlinear superposition formula of the solutions, the new infinite sequence solutions are constructed, consisting of Jacobi elliptic function solutions, hyperbolic function solutions and trigonometric function solutions of the generalized BBM equation.

the second kind of elliptic equation,the nonlinear superposition formula of the solutions,the new infinite sequence solutions

E-mail: 379338089@qq.com

10.6052/1672-6553-2015-62

2014-12-19收到第1稿,2015-06-22收到修改稿.

*国家自然科学基金资助项目(11361040)、内蒙古自治区高等学校科学研究基金(NJZY16180)和内蒙古自治区自然科学基金(2015MS0128)资助的课题