考查全面分析透彻对症解析
☉山东省济宁市实验初中董龙祥
考查全面分析透彻对症解析
☉山东省济宁市实验初中董龙祥
近年来,以几何图形的运动为载体,求几何图形在运动过程中,图形上某一动点所经过的路径的长度的题目在中考试卷常有出现.由于点随整个几何图形的运动而运动,其背景模糊,轨迹不明,它对分析问题的能力要求较高,它能全面考查数学活动过程,考查通过数学思考解决问题的综合应用能力,因而倍受各地中考命题者的青睐.解决这类问题时,首先要弄清在运动过程中,要求动点所形成的路径的形状是什么图形,然后根据运动的初始与终结位置确定相应动点的起点和终点,再根据相关计算公式计算出路径的长.其中分析动点所形成的路径的形状是解决问题的关键,也是解决问题的难点,由于初中阶段受知识局限性的影响,常见的有线段和圆弧,本文拟通过几道中考试题加以解析,从中体会这类试题的特点.
一、线段型
1.动点在一次函数的图像上
例1如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,同时出发,运动时间为t,当其中一点到达端点时,另一点也随之停止运动,在整个运动过程中,线段PQ的中点M所经过的路径长为______.
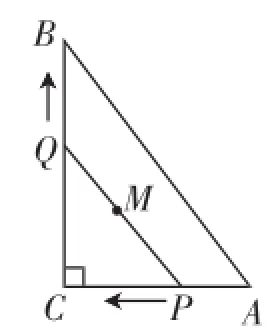
图1
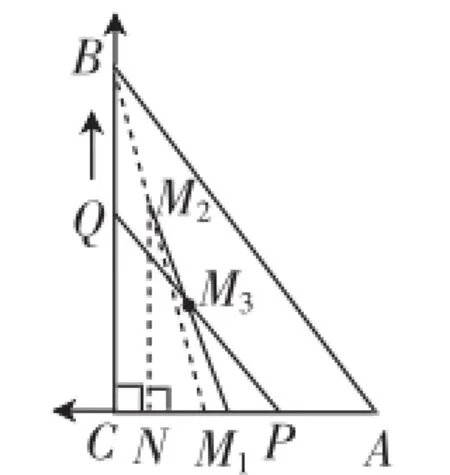
图2
解析:如图2,以C为原点,以AC所在的直线为x轴,建立平面直角坐标系.
因为点Q(0,2t),P(6-t,0),所以线段PQ的中点M的坐标为,所以
消去t得y=-2x+6,即动点M必在直线y=-2x+6上.
当t=0时,点M1的坐标为(3,0),当t=4时,点M2的坐标为(1,4),所以动点M所经过的路径为线段M1M2.
过点M2作M2N⊥x轴于点N,则M2N=4,M1N=2,所以
2.动点在线段的垂直平分线上
(1)把抛物线C1沿着直线AC方向平移到某处时得到抛物线C2,此时点A、C分别平移到点D、E处.设点F在抛物线C1上且在x轴的下方,若△DEF是以EF为底的等腰直角三角形,求点F的坐标.
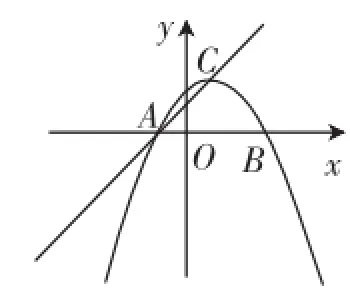
图3
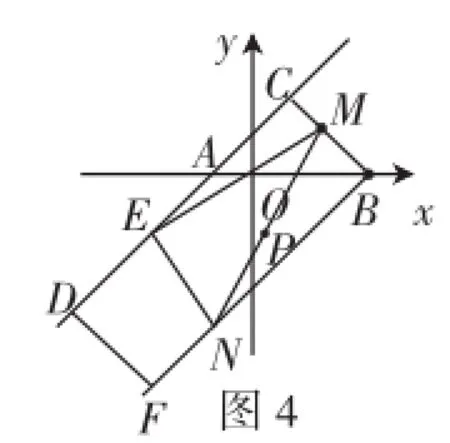
图4
(2)如图4,在(1)的条件下,设点M是线段BC上一动点,EN⊥EM交直线BF于点N,点P为线段MN的中点,当点M从点B向点C运动时求点P经过的路线长.
解析:(1)F(-3,-6).(过程略)
(2)易证四边形BCDF为矩形,所以∠MBN=90°.如图5,连接PE、PB,根据直角三角形斜边上的中线等于斜边的一半,得,所以PE=PB,所以点P在线段BE的垂直平分线上.
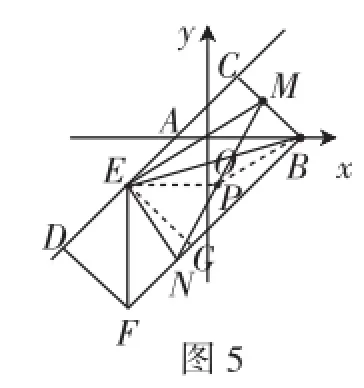
图5
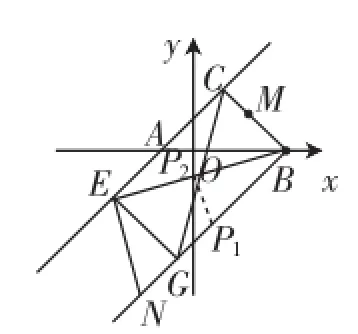
图6
如图6,当M与B重合时,点P在BN的中点P1处;
当M与C重合时,点P在BE的中点P2处;
所以P1P2为△BEN的中位线.
3.动点在已知直线的平行线上
例3如图7,M、N是线段上的两点,AB=8,AM=BN= 1,P为线段MN上的一个动点,分别以AP、BP为边在同侧作正方形APDC和正方形BPEF,G、H分别是边CD、EF的中点,当点P从M到N的运动过程中,线段GH的中点O所经过的路径长为_____.
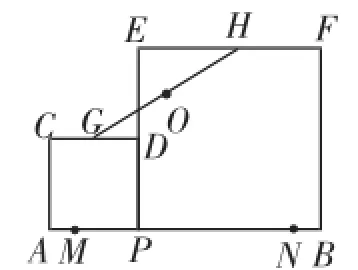
图7
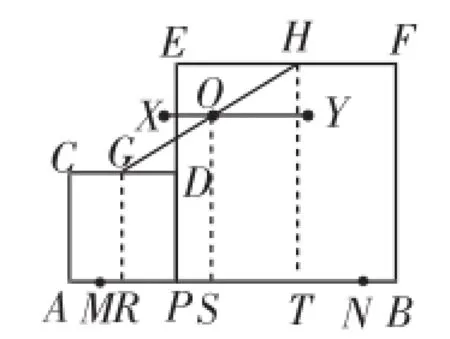
图8
解析:如图8,分别过点G、H、O作AB的垂线,垂足分别为点R、T、S,则四边形GRTH为梯形,因为O为GH的中点,由平行线等分线段定理得RS=ST.
所以点O的运动路径在与AB距离为4的平行线上.
当P与M重合时,点O在点X处;当P与N重合时,点O在点Y处.
所以点O的运动路径为线段XY,而点X到AC的距离为2.5,点Y到AC的距离为5.5.
所以XY=3,即线段GH的中点O所经过的路径长为3.
4.动点在同角的同一边上
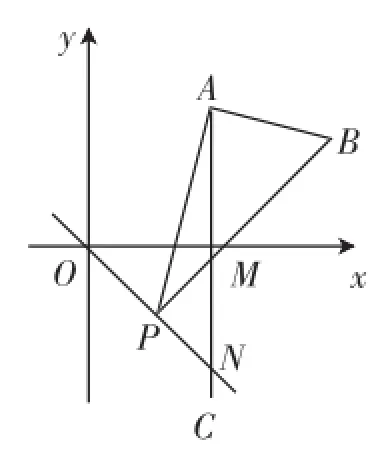
图9
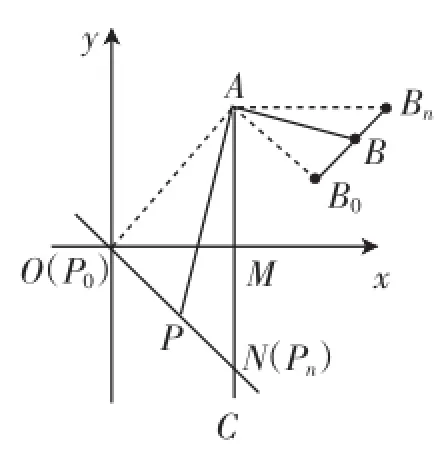
图10
解析:如图10,当点P在起点O时,此时点B记为B0;当点P在终点N时,此时点B记为Bn.
因为在Rt△APB中,∠APB=30°,∠PAB=90°,所以
因为∠OAB0=∠PAB=90°,所以∠OAP=∠B0AB.
同理可得∠AB0Bn=∠AON,所以∠AB0B=∠AB0Bn,所以点B在B0BN上,即点B的运动路径为线段B0Bn.
由此,几何中动点产生直线的形式多样,求解时离不开几何的一些“基本定理”和“基本图形”,常见“线段的垂直平分线性质的逆定理、角平分线性质定理的逆定理,以及等距平行线和等角共线”,回归一次函数的图像,动点的坐标必满足某个一次函数解析式,特别是易用含字母的代数式表示动点的坐标时可考虑此法.
二、圆弧型
1.动点到定点的距离等于定长
A.直线B.抛物线
C.圆D.反比例函数的曲线
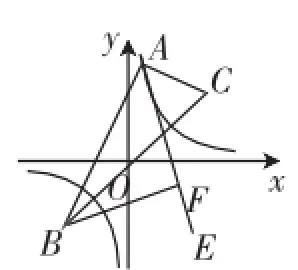
图11
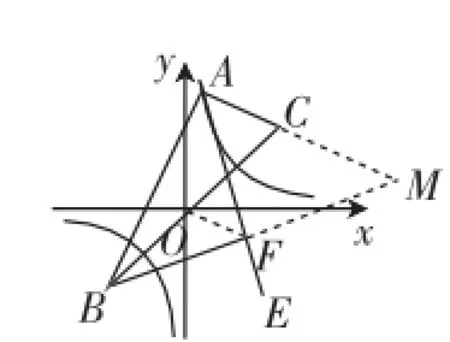
图12
解析:如图12,延长BF交AC的延长线于点M,连接OF.
因为AE平分∠BAC,AE⊥BF,所以∠ABF=∠AMF.
所以AB=AM,BF=MF.
2.动点为定线段所对的直角顶点
例6如图13,四边形ABCD、BEFG均为正方形,AB=2,G为AB的中点,现将正方形BEFG绕顶点B逆时针旋转(如图14),记直线AG与CE的交点为H,则当正方形BEFG绕顶点B旋转60°时点H所经过的路径长是______.
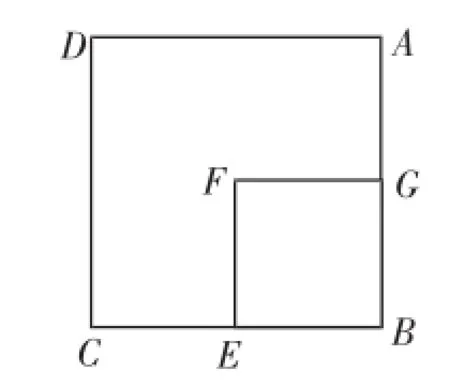
图13
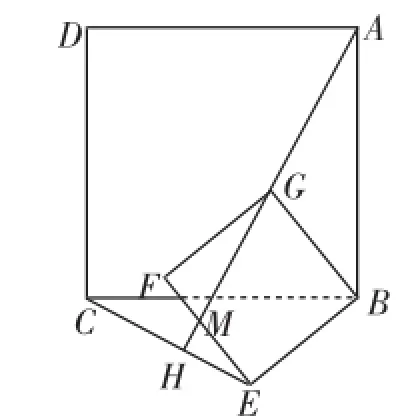
图14
解析:在△ABG和△CBE中,AB=CB,∠ABG=∠CBE,GB=EB,所以△ABG≌△CBE.所以∠BAG=∠BCE.因为∠BAG+∠AMB=90°,∠AMB=∠CMH,所以∠BCE+∠CMH= 90°,所以∠CHM=90°,即∠CHA=90°,所以点H在AC为直径的⊙O上(如图15).
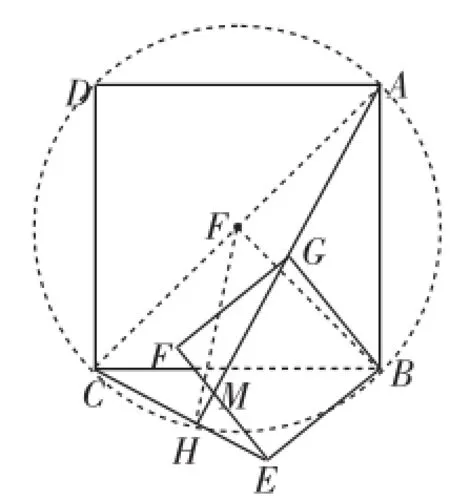
图15
当正方形BEFG绕顶点B逆时针旋转60°时,∠ABG= 60°,BG=1,AB=2,易证∠BAG=30°.
因为∠ABC=90°,所以点B在以AC为直径的⊙O上.
根据圆周角定理得∠BOH=60°,所以点H所经过的路径为以O为圆心,为半径,圆心角为60°的一段弧.
3.动点为定线段所对的定角顶点
例7如图16,半径为2cm,圆心角为90°的扇形OAB的A(B上有一运动的点P,从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在A(B上从点A运动到点B时,内心I所经过的路径长为______.
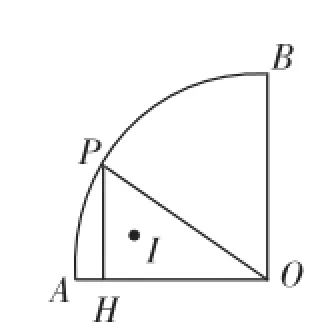
图16
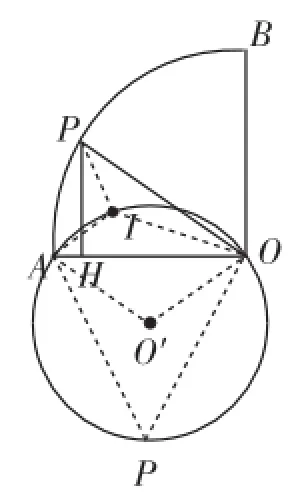
图17
解析:如图17,连接OI,PI,AI,由△OPH的内心为I,可得到∠PIO=180°-∠IPO-∠IOP=180°-(∠HOP+∠OPH)=135°.
因为OP=OA,∠IOP=∠IOA,OI=OI,所以△OPI≌△OAI,所以∠AIO=∠PIO=135°,所以点I在以OA为弦,并且所对的圆周角为135°的一段劣弧上.
过A、I、O三点作⊙O′,如图17,连接O′A,O′O,在优弧AO取点P,连接PA,PO,可得∠APO=180°-135°=45°,得
由此,动点为定线段所对的直角顶点产生圆,其本质是利用直角三角形斜边上的中线等于斜边的一半而得到动点到定点的距离等于定长,回归圆的定义,亦可理解为“直径所对圆周角为直径”的逆命题;动点为定线段所对的定角顶点产生圆,更具有一般性,只需在一个动三角形中满足“定边对定角”,角不一定是特殊的直角,亦有“圆”.
综上所述,几何动点路径问题需要挖掘隐含条件和潜在信息,理性分析运动过程中所保持的不变性质,在此过程可通过画图(起点、终点、中间关键点)判断路径形状和范围,然后通过数学方法进行分析验证及几何建构进行转化.H

