前测备课自主探究感悟收获——“配方法推导一元二次方程的求根公式”思考与感悟

☉江苏省无锡市东亭中学许丽芳

前测备课自主探究感悟收获
——“配方法推导一元二次方程的求根公式”思考与感悟

☉江苏省无锡市东亭中学许丽芳

一、理论与背景

布卢姆的建构主义理论对有效教学曾经提过三个经典的问题：教师准备把学生带到哪里去？教师通过怎样的手段带学生走过去？你的学生已经到指定位置了吗？这三个问题抽象出来就是：（1）这节课的教学目标是什么；（2）教学过程与方法如何设计；（3）学习结果如何进行有效评估.以皮亚杰为代表的建构主义也认为，在设定目标的前提下，学习的有效性建立在学生主动参与的前提下，即学生进行自主探究和合作为中心的学习是最好的学习方式，有助于发挥出学生的主动性和创造性.基于以上认识，笔者以“配方法推导一元二次方程的求根公式”一课为例，在进行教学前测以后，调整教学目标，让学生自主进行探究，直至收获课堂的精彩.

二、内容剖析与前测

求根公式的推导是引出根的判别式、进一步讨论一元二次方程的实数根的存在性的前提，同时也为推导根与系数的关系及今后学习二次函数等有关内容奠定基础.由于公式的推导均为字母间的运算，为了让学生能够亲自参与推演求根公式的过程，设计了4个活动，逐步由数字系数的一元二次方程过渡到含三个字母系数的一元二次方程，学生经历从特殊到一般的研究过程.本节课之前，笔者对自己所任教的九年级两个班共计72位同学做了一次调查，用配方法解方程：ax2+bx+c=0（a≠0），正确率仅约为4.17%，于是进行了简单分析.

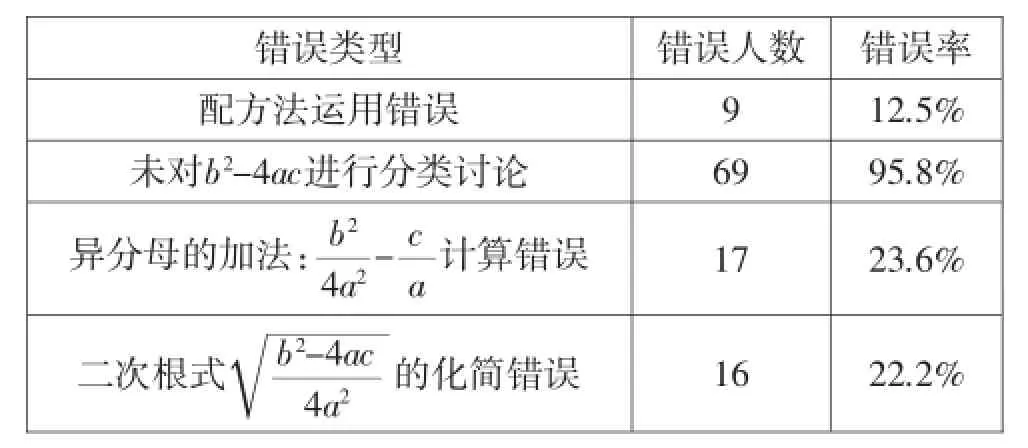
错误类型错误人数错误率配方法运用错误9 12.5%未对b2-4ac进行分类讨论69 95.8%异分母的加法：b24aa计算错误17 23.6%二次根式b2-4ac 4a 2-c√的化简错误16 22.2% 2

同时，设置了问题：在运用公式法解一元二次方程时，你有哪些困惑？有些学生认为公式的结构复杂，不便于记忆，主要靠死记硬背，套公式解一元二次方程，而不知公式从何而来.基于以上分析和调查，笔者认为虽然课标中并未对用配方法推导一元二次方程的求根公式提出具体要求，但推导过程本身的价值在于通过让学生亲历公式的推演，帮助学生理解一元二次方程的根是由系数a、b、c决定的.由于公式的推导过程均为字母间的运算，对学生来说困难较大，因此本节课的难点是：一元二次方程求根公式的推导过程.

三、教学设计与实施

为了达到教学目标，笔者把教学过程设计为以下五个阶段：

【活动1】请每组同学编一道一元二次方程，并用配方法求方程的解，填写以下表格：

所编方程文字表述步骤每步依据

同组的同学互相检查、纠错.数字系数的一元二次方程在求解过程中，由于计算原因不易发现各项系数及常数项对根的影响，因此，我们可以尝试着将方程中的系数一般化，用字母代替.一起看下面的表格：下面我们主要研究方程中仅含有一个字母系数的情况.在解之前，我们能否预想一下这三个方程哪一个最容易解，哪一个又是最不容易解的？

abcax2+bx+c=0（a≠0）

a11ax2+x+1=0

1b1x2+bx+1=0

11cx2+x+c=0

1bcx2+bx+c=0

a1cax2+x+c=0

ab1ax2+bx+1=0

【活动2】每组同学在以下方程中任选一个用配方法求解：

（1）x2+x+c=0；（2）ax2+x+1=0（a≠0）.

交流：配方后的结果是含有字母的代数式，首先要保证该代数式的值是非负的，因此要注意分类讨论.以（2）为例，学生进行讨论分析，让学生进行板演等活动，发挥学生的主体性，选取其中一位学生的解题过程.

解：由于a≠0，所以方程两边同时除以a，得：

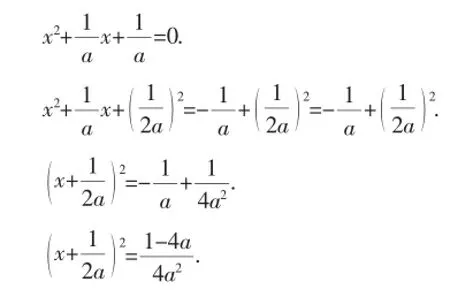
所以当1-4a≥0时，原方程的根为：

当1-4a＜0时，原方程无实数根.

在此，教师进行归纳并指出：对于以上两个方程，如果我们任意给出相应字母的值，就可以省去配方的过程，首先判断方程是否有实数根，如果有，直接代入根的表达式即可求出.对于任意的一元二次方程，要想知道方程的根与系数的关系，需要我们研究更为一般的形式，即形如ax2+bx+c=0（a≠0）的方程.

【活动3】用配方法解方程：ax2+bx+c=0（a≠0）.

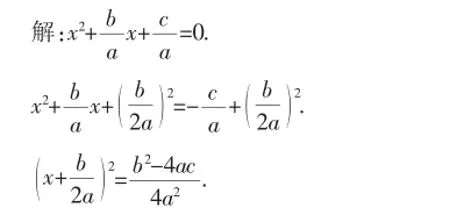
由a≠0，得a2≠0，则可判断a2＞0，故4a2＞0.

因此只需当b2-4ac≥0时，开平方，得：

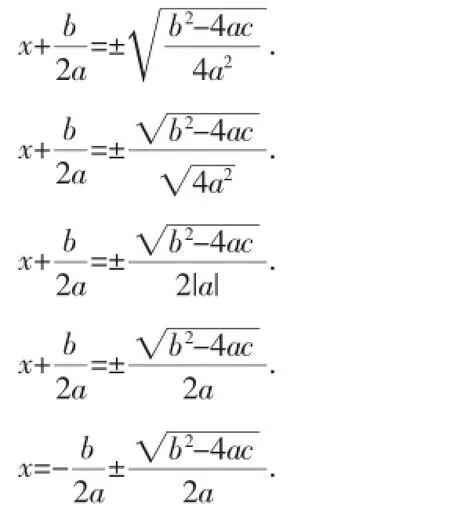
原方程的解为：

当b2-4ac＜0时，原方程无实数根.

通过前面的探索，我们得到了一元二次方程ax2+bx+ c=0（a≠0）的求根公式：

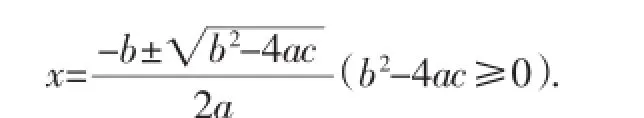
总结：用求根公式解一元二次方程的流程图：

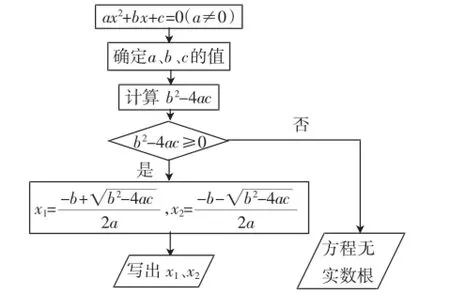
所有的一元二次方程都可以用配方法求解，所以这是一个通法，有规律可循.如果我们不抽象、概括出一个数学模型，那么每次都要做重复性的工作.抽象、概括正是数学学习留给我们的思维品质；同时，一元二次方程的求根公式向我们揭示了方程的根与各项系数间的内在联系.下面从公式的结构进行分析：从运算的角度看，公式包容了初中阶段所学过的全部六种代数运算：加、减、乘、除、乘方、开方，体现了和谐统一.通过运算可以完美地解决根的存在性、根的个数、根的求法三个问题，可以说是“万能”求根公式.它向我们展示了抽象性、一般性和简洁性等数学的美和魅力.如果一元二次方程有两个不相等的实数根，这两个根之间只有细微的差别，我们在以后的学习中会继续探索一元二次方程根与系数的关系.

【活动4】感悟与收获（以问题形式给出）.

问题：这节课我们学习了什么知识？有何作用？运用本节课所学知识解决问题时要注意些什么？这节课我们学到了解决数学问题的哪些方法？运用了哪些数学思想？

四、体验与感悟

本课尝试进行了教学前测诊断，通过诊断指导教学过程，意在使学生通过配方，感知一元二次方程中系数与根之间的联系.另外，分式运算、二次根式化简也是学生感到困难的地方.

1.结合诊断分析，合理设计教学

在讲授这节课之前，笔者首先对已经学习求根公式的学生进行了调研，发现绝大多数学生不会用配方法推导一元二次方程的求根公式，对学习求根公式的意义不理解.只觉得背求根公式麻烦，容易记混淆，因此在解题时部分学生不愿意用求根公式解题.于是笔者在调研的基础上，进行了详细地分析，发现了学生学习中存在的主要问题，同时对所任教班级学生的基础知识、思维特点、探究意识等方面进行了认真地分析，根据学生的具体情况和教学内容特点合理设计教学.学生动脑、动手，感受学习求根公式的意义，让学生知道“为什么学”.教学环节的设计及教学问题的提出符合学生的知识结构和认知规律，符合因材施教原则.

2.抓住数学本质，提升数学素养

数学教学的根本是公理化和程序化，本节课是将一元二次方程的求解过程程序化.教学中吴老师引导学生不断将一元二次方程的系数一般化.首先让学生自己编写一个数字系数的一元二次方程，小组合作确定求解，然后小组展示交流，让学生体会编写题目的系数不同，求解的结果就不同，甚至有的题目无解，感受方程系数直接影响方程根的情况，然后带领学生把方程的系数逐步一般化，使方程中出现一个字母系数、两个字母系数直至三个字母系数的情况.让学生自由选择用配方法解题，使不同层次的学生都能获得成功的喜悦，同时也为方程中含有a、b、c三个字母的一般方程配方推导作好铺垫.可见，教师不断引导学生认识到程序化的优势，减少做重复性的工作，使学生逐步认识学习求根公式的必要性和价值，抓住了数学的本质，提升了学生的数学素养和思维品质.

3.注重自主探究，体现学生主体

这节课整体感觉是教师在不断与学生沟通交流中完成教学任务的.在尊重学生人格的基础上更加尊重学生的思维，小组合作学习落到实处，为了使每个同学都积极地、有效地参与到学习中去，使本来枯燥乏味的教学内容变得有趣，教师在教学中设计了学生自己编题与小组为单位自主选题，然后展示、交流相结合，激发学生学习的主动性，提高学生数学学习的兴趣，发挥学生的主体作用.总之，这节课的设计基于建构主义理论，关注了学生的认知规律，调动了学生数学学习的主动性，让学生充分地参与课堂教学，真正把课堂还给学生，注重求根公式的推导过程.从学生已有的知识结构和认知结构入手，进行教学设计，问题设计由简到繁、由易到难、由具体到抽象，使不同学生在数学上都能有不同程度的进步.Z