例析线性规划中常见目标函数的数学模型

☉江苏省南通市通州区金沙中学　陈　刚

例析线性规划中常见目标函数的数学模型

☉江苏省南通市通州区金沙中学陈刚

线性规划是高中数学必修5不等式章节中的内容，高考中常见的问题类型有关于目标函数最值求解、目标函数取值范围、约束条件中参数范围、整点问题和可行域面积等一类.其中前两类是有关于目标函数的问题是各种考试中出现频率较高的类型.对于这类问题有两个难点：其一，识别问题中线性规划的问题本质，出题人考查线性规划，并不死板直接给出线性压缩条件来求解目标函数取值，而是给线性规划加一层“外衣”让学生无法直接判定利用线性规划解决；其二，判别目标函数的数学模型，对于这类问题另一个关键点在于识别目标函数的类型，以便采取相对应的策略，而对学生而言，很难想出行之有效的方法来处理目标函数，其关键原因是他们无法判别目标函数的数学模型.扫描线性规划中与目标函数取值相关的问题，可以发现常见的目标函数有z=2等几种形式.观察这几个式子的形式特征，其实不难发现每个式子都有其对应的数学模型，分别对应面积模型、斜率模型、截距模型和点距模型.文章试图以理论与实例结合的方式来阐述线性规划中常见的四种目标函数.

一、z=xy：面积模型

理论分析：目标函数z=xy中的x，y分别代表了可行域中点的横、纵坐标，从几何学的角度来看，x与y乘积的几何意义是坐标轴与点的横纵坐标线围成的矩形的面积.当x与y之间存在一定的数量关系时，可以利用这个等量关系进行消元，将目标函数中的两个未知数转化成一个关于x或y的表达式，从而通过求解函数取值范围的方式来求目标函数的最值或取值范围.

解析：函数在某个区间上单调递减表明函数的导数在这个区间上小于0恒成立，因此，本题可表达成导函数f′（x）≤0在区间上恒成立，从而可列出关于m和n的不等关系式，以此不等关系式为线性压缩条件画出可行域，并寻找目标函数k=mn的最优解.

导函数f′（x）=（m-2）x+n-8，明显导函数是一次函数或常数，要求导函数f′（x）≤0在区间上恒成立，即保证其最大值为小于等于0，所以保证f′（2）和同时小于0，即以此为线性压缩条件，绘制如图1所示的可行域.显然，此线性规划的最优解应当在两条直线上.两条直线的交点为（2，8），所以当m∈（0，2）时，mn=9m-当m∈（2，6）时，mn=12m-2m2，mn可以写成分段函数的形式：mn=此分段函数在m=3时取最大值18.

图1　

实例说明：（2012年江苏高考14题）正数a，b，c满足：5c-3a≤b≤4c-a，clnb≥a+clnc，求的取值范围.

解析：由于a，b，c均为正数，所以将题设中不等式同时除以c，可得，而换元后原不等式转化为不等式组画图2所示的可行域可看成看成可行域中的动点与原点构成直线的斜率，图形可知当直线与y≥ex相切时斜率最小为e，当直线过两条直线交点（0.5，3.5）时斜率最大为7，所以

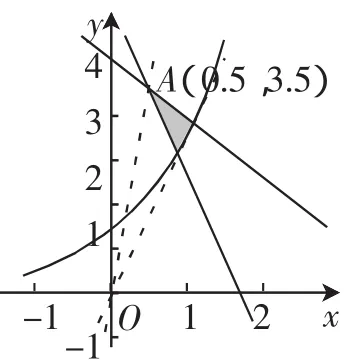
图2　

三、z=mx+ny（n≠0）：截距模型

理论分析：将目标函数z=mx+ny（n≠0）的表达形式略作调整变形为，此时可将z看作是直线y=的纵截距相关的量，要求z的取值范围（或最值），即求直线纵截距在线性压缩条件下的取值范围（或最值）.需要注意的是当n为正数时，z的最大值在纵截距最大时取，最小值在纵截距最小时取；当n为负数时，z的最大值在纵截距最小时取，最小值在纵截距最大时取.

实例说明：（2014年合肥校级模拟）定义在R上的函数y=f（x）是减函数，且对任意a∈R都有f（-a）+f（a）=0，若x，y满足不等式f（x2-2x）+f（2y-y2）≤0，当1≤x≤4时，求z= 2x-y的最大值和最小值的最优解.

解析：由y=f（x）对任意a∈R都有f（-a）+f（a）=0，可知y=f（x）为定义在R上的奇函数.又f（x2-2x）+f（2y-y2）≤0，所以f（x2-2x）≤f（y2-2y）.因为函数为定义在R上的减函数，所以x2-2x≥y2-2y，整理后可得（x+y-2）（x-y）≥0，线性压缩条件为得图3所示的可行域.将目标函数改写成y=2x-z，因此，当z取最大值10时，最优解为（4，-2），z取最大值1时，最优解为（1，1）.

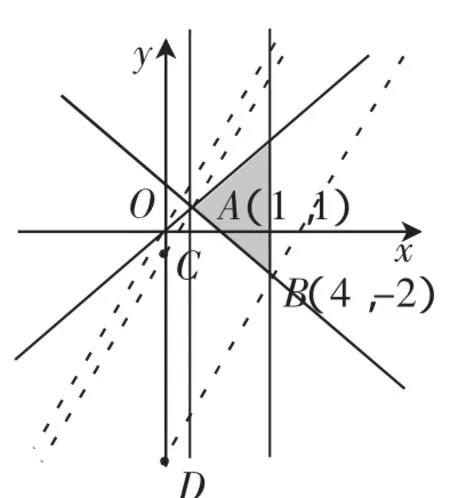
图3　

四、z=（x-a）2+（y-b）2：点距模型

理论分析：目标函数的表达形式与解析几何中两点之间距离公式相似，所以目标函数的几何意义可解读为两点之间距离的平方.因此，根据目标函数表达式的几何意义，可以将目标函数理解成可行域中的任意一点（x，y）与定点（a，b）之间的距离的平方，对于这种与两点之间距离公式相关的目标函数，我们将其的数学原型称为点距模型.

实例说明：（2014年东港区校级模拟）已知方程x2+ ax+2b=0（a，b∈R）一根在区间（0，1）之间，另一根在区间（1，2）之间，求z=（a+3）2+b2的取值范围.

解析：令f（x）=x2+ax+2b，由实根分布的知识可知，函数的两个零点分别在区间（0，1）和（1，2）代表f（0）>0， f（1）<0，f（2）>0三者同时成立，即

以a为横坐标，b为纵坐标，画出可行域，如图4，当a=-1，b=0时，zmax=4；当a=-2.5，b=0.5时，zmin=0.5.由于边界取不到，所以z∈（0.5，4）.

回顾上述几道典型的例题可以发现每道题都不是直接给定可行域，而是以另外一种知识背景出现，然后回归到线性规划的本质.因此，数学问题常常会带有一定的伪装性，为了让学生不能够直接判断要使用哪一种类型的知识点，出题人常常会为试题带上一些“面具”，例如上文四例就分别以导数、不等式、函数性质和实根分布表面知识为背景，来考查线性规划的本质.然而这恰恰是数学美丽的地方，灵活多变的外表却隐藏着同一个本质.

图4　

1.张红菊.剔除干扰因素还原本来面目——不同视角下线性规划问题的求解［J］.高中数理化，2015（19）.