善于提问：基于习题教学的视角

☉江苏省张家港市护漕港中学陈桂芬

善于提问：基于习题教学的视角

☉江苏省张家港市护漕港中学陈桂芬

华东师大钟启泉教授在《“教会提问”的教学》一文中指出：“‘提问’的特征是懂得的人（教师）问不懂得的人（儿童）.这跟日常不懂得的人向懂得的人的发问，形成了鲜明的对照.正因为如此，在提问之际，必须明确地意识到为什么而问.”根据上述观点，我们思考了习题教学中的提问角度，本文就基于日本教育心理学家佐伯胖归纳的教育现场的经验，结合近年来习题教学的案例，解读提问视角与反思教学立意，与同行研讨.

一、促进深思的提问案例与意图解读

（一）改变视点的提问

题例1：如图1，∠MON内有一点A.

（1）过点A画AB∥ON交OM于B，画AC∥OM交ON于C；

（2）过点M画MH⊥ON，垂足为H；

（3）在上面画图的基础上，度量、比较（用“=”“＞”“＜”填空）：∠MON_______∠BAC；OB______AH.

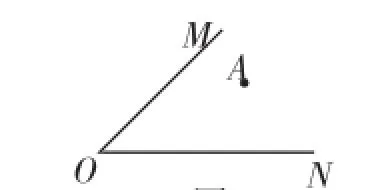
图1

预设追问：如图2，直线BE、CD相交于点A，且CD∥OB，AB∥ON.

图2

追问1：若∠MON=45°，求∠ACN的度数；

追问2：若∠DAE=45°，求∠MON的度数；

追问3：像（2）中的∠BOC、∠BAC称为四边形ABOC的一组“对角”，则该四边形的另一组对角相等吗？说明理由.

追问4：小睿同学提出一个命题：如果一个角的两边与另一个角的两边分别平行，那么这两个角一定相等.请直接判断这个命题是真命题还是假命题.

设计意图：初看后续4个追问，貌似与前面的题例没有关联，其实在前面题例画图的基础上，已经得到如图2所示的图形，所以我们的“追问”实际上是围绕学生已画出的图形展开提问，也即改变视点的提问，把学生对这个图形的认识引导到平行线的性质与判定的研究上来，并且在最后一问设计了一道判断真假命题的较难问题，然而答案又恰恰在图2中，因为在图2中既能找到正例，也能找到反例.

（二）引进别的假定的提问

题例2：请结合夏新同学的收支情况表，思考下面的问题：

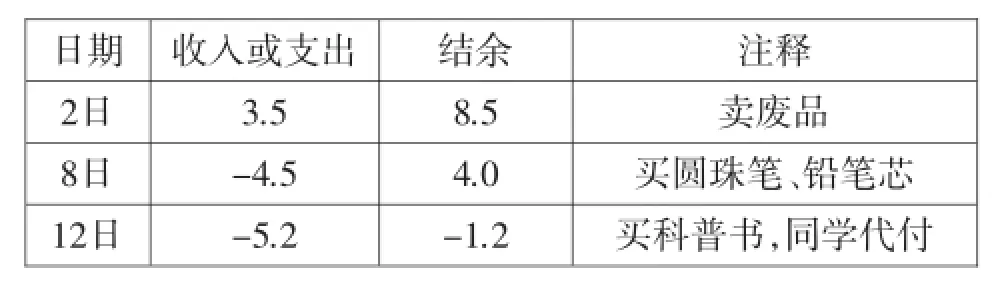
收支情况表

这是教材上容易找到的一个生活情境，我们在课前预设了如下的一些问题.

问题1：请将表格中第2、3列的6个数据分成两个集合，注明分类依据；

问题2：从表格中可发现算式：8.5-4.5=4.0，类似地，请再写出一个算式：________________；

问题3：小敏同学经过思考，发现了夏新同学在2日之前的零花钱数，你知道她是怎么想的吗？

在学生成功解答上述问题之后，我们再引入目前较为流行的一种“新定义考题”，如问题4.

问题4：给出定义：给出两个数a、b（a＞b），当a-b≤1时，称（a，b）为“相邻数对”，a-b为“相邻数差”.如上面表格中的（4.0，3.5）就是“相邻数对”，此时“相邻数差”为0.5.

请写出表格中另外的“相邻数对”及“相邻数差”.

设计意图：针对一个生活现实，追求设问的角度多样化.从本质上说，就是倡导开放式数学教学，把学生的思考引向“四面八方”.

（三）举出例子的提问

题例3：在数轴上，点A、B分别对应着数a、b.

（1）①当a=2，b=6时，AB=_______；

②当a=-6，b=-2时，AB=_______；

③当a=____，b=_____时，AB=_______.（写一组符合要求的即可）

（2）用含a、b的式子表示AB.

（3）式子|3-2|或|2-3|的图形意义可以是：数轴上表示3、2的两点之间的距离.

的图形意义：_____________________；

|2+5|的图形意义：_______________________.

设计意图：初一学习数轴时，为了引导学生数形结合地分析问题，预设了上述问题，也是为了学生积累数轴上两点之间距离公式而研制，同时还导引着后续平面直角坐标系中两点距离公式的基础.上面的（3）是结合数轴进行理解，其实我们还可通过恰当的设计，引导学生给出反例，比如在八年级学生学习了特殊等腰三角形性质之后，我们曾提出如下问题.

练习期间，小舟“发现”一个猜想：如果直角三角形中有两边之比为1∶2，则该直角三角形中必有一锐角为30°！请判断小舟同学的“发现”命题的真假.如果是真命题，给出证明；如果是假命题，给出反例.

设计意图：这个问题就是让学生举出反例，训练学生的批判性思维.

（四）思考案例的提问

题例4：（1）求下列各数的算术平方根：①0.0025；②81；③32.

设计意图：这是初学平方根后的一组运算练习，一般来说，新接触一类数后，学习套路通常是这类新数的定义及相关概念，接着是这类数如何运算，所以这里安排一组化简与简单运算，就是遵循这样的学习套路，在此基础上，我们还可增加如下的追问.

追问：有同学在练习两个无理数的运算后发现：两个无理数相加（减），结果一定是无理数；而两个无理数相乘，结果却难确定.你怎么看这个同学的“发现”？建议举例后再配文字阐述你的观点.

追问意图：通过这一追问，促进学生运算后的反思经验，追求成果扩大，本质上是对实数运算是否封闭的深入思考.

（五）抽丝剥茧的提问

题例5：如图3，△AOB中，A、B两点的坐标分别为（2，4）、（6，2），求△AOB的面积.

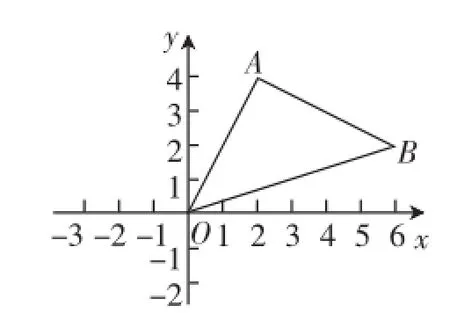
图3

（1）用两种方法求三角形AOB的面积.

（2）小舟同学发现：过点B作y轴的垂线交AO于P，这时把三角形AOB分割成两个三角形……也就能求出面积了！你能否完善这种思路？

设计意图：这是学生初学平面直角坐标系后的一道习题，鼓励学生从不同角度计算三角形面积之后，我们还可把设问视角“引向他处”，比如促进学生发现特殊图形，追问如下.

追问：小杰经过度量发现，三角形AOB好像是个等腰直角三角形，……结合上面求出的面积就可以求出AO、BO的长……你能否完善这种思路.

追问意图：学生虽然此时还没有勾股定理的知识储备，但是可以利用三角形面积与数的开方等知识来作出解释，通过这一追问，抽丝剥茧，让学生复习“一条主线”上的数学概念和性质.

（六）提示矛盾的提问

题例6：思考：x取哪些整数值时，2≤3x-7＜8成立？

（1）解不等式2≤3x-7；

设计意图：这是一道基础习题，初学不等式之后学生应该都能掌握，为了变换问题呈现的形式，多角度启发学生思考，我们还预设了如下两个追问.

追问1：小舟认为：不转化为不等式组，也可以直接

解2≤3x-7＜8！你觉得小舟同学是怎样解的？

小舟看到后，就指出小杰第一步就出错了！……

你知道错误原因是什么吗？请求出2x≤3x-7＜8的解集.

追问意图：通过引入错漏解法，让学生参与辨析，学会诊断、纠错与究错，融错于学习中.顺便指出，还有一类应用问题本身由于记录有误，也是引发矛盾很好的题例，请看链接习题.

链接习题：【帐目阅读】某家商店的帐目记录显示，某天卖出26支牙刷和14盒牙膏，收入264元；另一天，以同样的价格卖出同样的39支牙刷和21盒牙膏，收入393元.

【倾听理解】该商店的会计人员稍加演算就发现上述记录有误！

【一起参与】请思考为什么上述记录有误.你能用二元一次方程组的知识来解释吗？

这个记录是否有误.如果有误，请说明理由.

（七）提示发现的提问

题例7：如图4，AD、BE、CF是△ABC的三条中线，若△ABC的周长是acm，当a=24时，求AE+CD+BF的值.

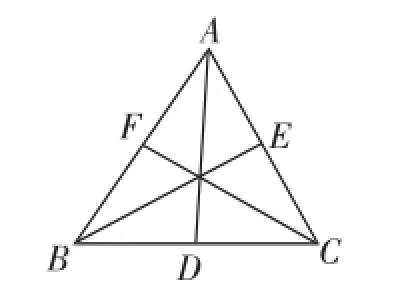
图4

设计意图：这是一道经典习题，利用中线性质，整体处理就可获得解答.关键是我们增设了如下追问，促进学生发现问题、成果扩大.

追问1：小杰完成练习之后，发现CE+BD+AF的值也能求出，你会吗？

追问3：设三条中线交于G点，小婧度量后发现：GE∶GB=GF∶GC=…，可是理由呢？你知道她发现什么了吗？

追问意图：这三个追问层层递进，前两问是从特殊到一般，最后一个追问更是隐含着三角形“重心定理”.

（八）变化条件的提问

题例8：如图5，四边形ABCD为矩形，过点D作对角线BD的垂线，交BC的延长线于点E，取BE的中点F，连接DF，DF=3.

（1）当F在BC的延长线上时，若AB=2，求矩形ABCD的面积.

（2）设AB=a，AD=b，请分析代数式a2+（b-3）2的值是否为定值？如果变化，说明理由；如果不变，求出这个定值.

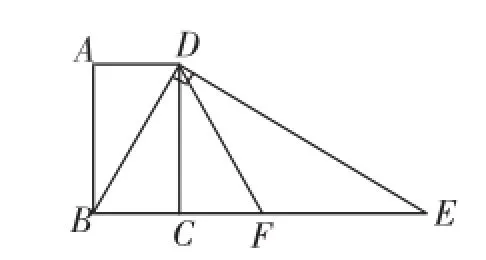
图5

设计意图：这是一次习题讲评课上针对一道2015年中考题的变式讲评，我们增设了（1），让学生从常量计算过渡到变量最值的思考，并且在（1）限制了点F在BC的延长线上，避免了分类讨论，事实上，对于优秀学生，我们还可跟进如下拓展思考.

拓展思考：若AB=1，画图分析矩形ABCD的周长.

这样就需要分不同情形进行讨论了，比如点F在边BC上，或点F在BC的延长线上.通过这样变化条件，从限制到开放，对学生缜密思维的考查就比较到位.

二、写在最后

从本质上说，本文关注的其实是命题基本功，所谓“教会提问”“善于提问”，都需要教师在“三个理解”上持续修炼，不断精进，既需要深入理解数学本质、数学基本思想，又需要理解学生，特别是不同学段学生的理解能力，还需要懂得教学，知道什么时候增加设问、追问是恰时恰点恰当的.当然，在这方面，知易行难，我们一起努力.

1.钟启泉.“教会提问”的教学［J］.基础教育课程，2014（9）.

2.鲍建生，顾泠沅，等.变式教学研究［J］.数学教学，2003（1，2，3）.

3.郑毓信.善于提问［J］.人民教育，2008（19）.

4.郑毓信.善于优化［J］.人民教育，2008（20）.

5.刘东升.对时育物，有效追问——浅论初中数学课堂教学中的追问艺术［J］.中学数学教学参考（中），2012（4）.Z