推陈出新求简洁,自然生长思关联
☉江苏省海安县城南实验中学刘东升
推陈出新求简洁,自然生长思关联
☉江苏省海安县城南实验中学刘东升
在近期教学实践中,笔者将一些叙述较为繁冗的“陈题”(这里的“陈题”是指在各级考题中反复出现,且在网络上百度一些关键词后很快会出现大量这样的雷同题),本着追求简洁的命题取向,将其改编后提供给学生练习,取得较好的训练效果.本文选取三个陈题改编的题例,并附改编意图与命题思考,提供研讨.
一、陈题与改编的题例呈现
陈题1探究题:如图1.
(1)△ABC为等边三角形,动点D在边CA上,动点P在边BC上,若这两点分别从点C、B同时出发,以相同的速度由C向A和由B向C运动,连接AP、BD交于点Q,求证:AP=BD;
(2)如果把原题中的“动点D在边CA上,动点P边BC上”,改为……,其他条件不变,请你利用图2的情形,求证:∠BQP=60°;
(3)如果把原题中的“动点P在边BC上”,改为……,如图3,则动点D、P在运动过程中,求证:DE=PE.
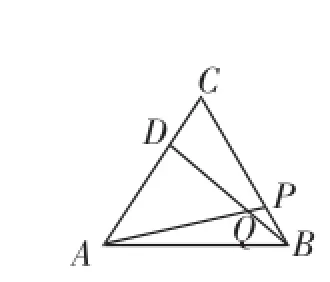
图1
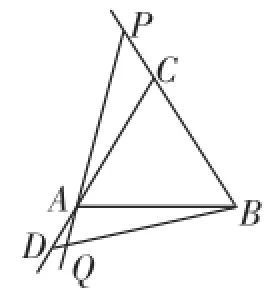
图2

图3
简评:该题陈述繁冗,表述不清,极容易造成误解,不符合数学试题追求简洁好懂、自然生长的高要求.考虑到该题在网络上非常流行,故摘引时第(2)、(3)问中部分条件以“……”取代,节约版面.以下给出改编题.
改编题1如图1,在等边△ABC中,点D、P分别在边CA、BC所在的直线上,直线BP、AQ交于点Q,且CD=BP.
(1)若点D、P分别在边CA、BC上时,求证:AP=BD;
(2)若点D、P在射线CA和射线BC上时,请利用图2求∠BQP的度数.
改编说明:将“陈题1”中第(2)问的变式统一在题干中,以条件“点D、P分别在边CA、BC所在的直线上”呈现,这样在第(1)问设置成特殊条件,强调“点D、P分别在边CA、BC上”,而在第(2)问中放开到射线上进行研究.事实上,随着探究的深入,如果作为习题讲评课,还可启发学生深入思考:如果点D、P在直线CA和直线BC上时,求∠BQP的度数.这样设问,则需要学生全面讨论,求解难度也将会上一个新的台阶.
陈题2如图4,在平面直角坐标系中,已知A(0,a),B(-b,0),且a、b满足
(1)求证:∠OAB=∠OBA.
(2)如图4,若BE⊥AE,求∠AEO的度数.
(3)如图5,若D是AO的中点,DE∥BO,点F在AB的延长线上,∠EOF=45°,连接EF,试探究OE和EF的数量及位置关系.
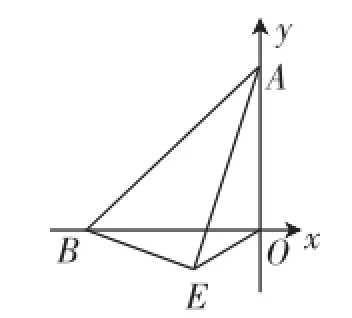
图4
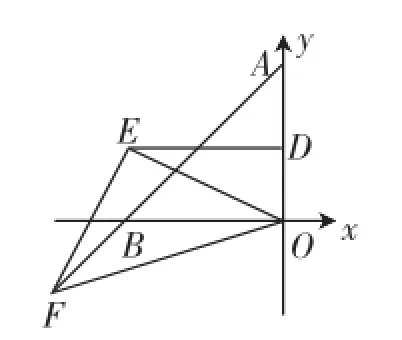
图5
简评:第(2)问就需要高超的构图能力,且表述也不清楚,并没有明确点E所在位置,图形也只是示意图;第(3)问陷入繁杂的图形构造,对于限时考试来说,这样的试题慎用为宜.基于以上商榷意见,笔者改编如下:
改编题2如图6,在平面直角坐标系中,已知A(0,a),B(-b,0),P(p,0),且a、b满足连接AB,作射线AP,过点B作BH⊥AP于点H.
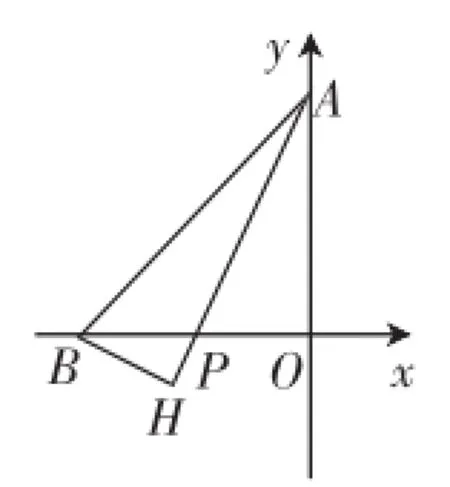
图6
(1)当p=-1时.
①填空:线段AP为△AOB的_____;(直接填“角平分线”、“中线”或“高”)
②延长BH交y轴于点C,求证:BC=AP.
(2)连接OH,求∠AHO的度数.
改编说明:首先是题干中明确了点P,善于读题的学生应该清楚点P是x轴上一个动点,则图6只是一个示意图,点H会随着点P的运动而变化;这为第(2)问的分类讨论带来启示.有效考查了优秀学生严谨的思维品质;同时对学生读句画图、构图能力也有较好的考查.
陈题3如图7,在四边形ABDM中,AB=BD,AB⊥BD,∠AMD=60°,以AB为边作等边△ABC,∠ABD的平分线BE交CD于点E,连接ME.
(1)求∠BEC的度数;

图7
(2)连接EA,求证:EC=ED+EB;
(3)求∠AME的度数.
简评:主要难点在第(3)问,需要较强的构图能力,这里提供两种构造思考,如图8、图9都能实现第(3)问的思路贯通.
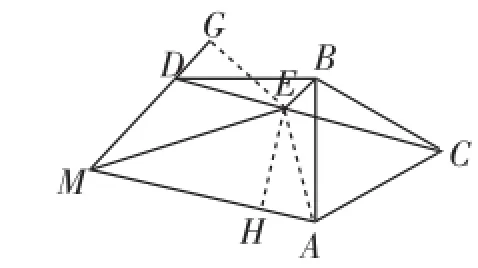
图8
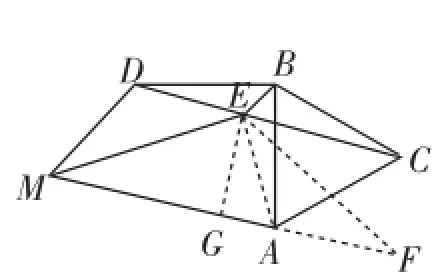
图9
然而,就本题的第(2)、(3)问来看,关联度并不紧密,且题干中的“∠AMD=60°”在前两问也没有多大价值,所以改编时,笔者放弃了第(3)问,只是对前面两问进行生长、拓展,改编为下面这道习题.
改编题3如图10,在△ABD中,AB=AD,∠DAB=90°,以AB为边作等边△ABC,∠BAD的平分线AE交CD于点E.
(1)求∠AED的度数;
(2)求证:EC=DE+AE;

图10
(3)在射线AE上求作一点P,使∠ABP=75°.(不写作法,保留作图痕迹)
改编说明:围绕将“陈题3”中的∠BAD的平分线AE进行了开发,并且在洞察了图形中很多特殊角度(如∠EDB=30°,连接EB,有∠EBD=30°)之后,在第(3)问提出尺规作图,使之满足“∠ABP=75°”,随着学生对图10中各个角度认识的深度,将会有不同的作法,这里作法的繁简与理解的深刻有直接的关系.比如,我们收集了三种典型的学生作法(图11、图12、图13).

图11
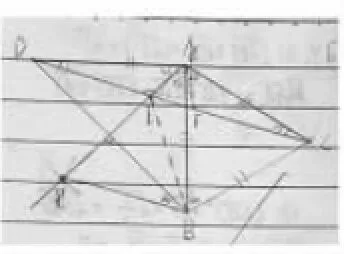
图12
图13
可以发现,在图11中,学生先作出一个60°角,再作60°角的平分线与AE相交于点P;图12中,学生以BE为一边,构造一个等边△BEP,恰好交点在AE上;图13中,学生只是“一道弧”就轻松搞定.事实上,笔者在相关数学研究QQ群是展示该题之后,有热心的同行还用几何画板提供了不同的“一道弧”作法(图14~17).
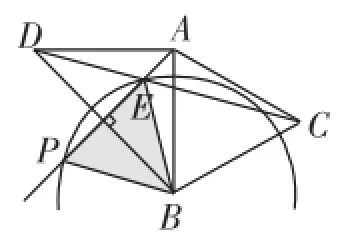
图14

图15

图16
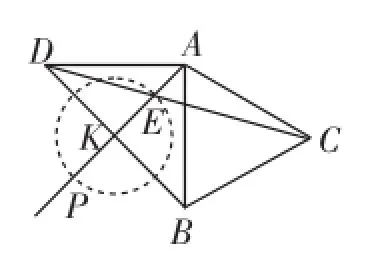
图17
二、关于陈题改编的三点思考
以上选取三个陈题及改编的题例,解读、商榷并阐释了陈题改编的心路历程,以下再从整体上就陈题改编提出三点初步思考.
1.理解陈题,有的放矢推陈出新题
何明老师在文1中将一道“双曲线”综合题从300多字(外加两个坐标系图形)减少到100字(没有图形),命题打磨过程中由博返约、追求简洁的示范意义让笔者受益良多.然而要想追求试题的简约呈现,需要我们在陈题改编之前,从不同角度贯通思路,提炼和洞察陈题的“深层结构”(罗增儒语).在此基础上还需要理解陈题系列设问的“并列”或“递进”.一般来说,作为一道解答题下的系列设问建议设计成并列式问题,但体现递进式求解的策略(详见文2).从这个角度来看,上文中的改编题2、改编题3都“有的放矢”地舍弃了陈题2、陈题3的第(3)问,正是想追求系列设问之间的递进式求解策略.
2.精心构思,题干题肢预设关联点
以上文中提及的陈题3来说,题干中的“∠AMD=60°”在前两问都没有得到体现,像这样的题干呈现就不符合简洁呈现的追求,可以作为第(3)问的一个强化条件,使得题干更趋于简洁好懂.这样看来,在预设一道解答题时,就需要认真构思题干、题肢的条件呈现,而不宜把所有条件都“全面铺开”,造成一些学困生阅读和理解障碍.以笔者教学实践来看,有些学困生在阅读信息量、错综复杂的条件时常常容易读漏或混淆条件,使得原本应该解答出来的第(1)、(2)问也不能顺利解出.至于有些同行提出训练学生从繁杂信息或条件呈现中“抗干扰”能力的考查要求,笔者则不敢认同,根本上说,这不符合“好的数学题目”应该“简洁好懂、自然生长”(章建跃语)的价值追求.此外,就题肢之间的关系来看,不仅要追求上面提及的并列式问题与递进式求解的思路暗示,还要思考题干信息与题肢之间的相容、包含或者逻辑连贯.比如,“改编题1”在题干中提到的是“点D、P分别在边CA、BC所在的直线上”,而两个题肢中分别是关于线段、射线的探究;再如,“改编题2”在题肢第(3)问中设计在射线AE上作出一点P,则让题干中的角平分线保持着“生命活力”,而没有让题干中这个重要条件“提前死去”.
3.易进难出,把关设问引向更远处
一般来说,解答题特别是作为全卷最后一题的把关题来说,应该努力追求易进难出,起点要低,吸引更多的学生参与.但是,作为最后一问又要使得问题具有必要的区分功能,就需要设计易错点、障碍处加大难度,通过恰当的把关设问把学生的思考引向深入、走向远处.比如,改编题1的第(3)问考查的是“点D、P在射线CA和射线BC上”,优秀学生在考后仍然可以思考“点D、P在射线AC和射线CB上”的情形;再如,改编题2的第(3)问“求∠AHO的度数”,如果学生只得到45°时,则说明思维还不够严谨,缺少考虑点P在x轴正半轴的讨论,教师在讲评时可以从点P坐标特征的角度引导学生“回到概念”,理解坐标轴是直线、x轴上点的坐标特征等角度来突破,这样重视“回到概念去解题”就能得到很好的落实.
1.何明.由博返约,追求简洁——一道“双曲线”综合题的命题过程[J].中学数学(下),2015(11).
2.刘东升.“并列”式问题与“递进”式求解——由一则解题教学案例说起[J].中学数学教学参考(中),2012(8).
3.刘东升.关联性:一个值得重视的研究领域[J].中学数学(下),2013(12).H

