预设系列问题串，注重关联式变式——以“双一次函数”习题课为例

☉江苏省苏州市高新区实验初级中学练兆明

预设系列问题串，注重关联式变式
——以“双一次函数”习题课为例

☉江苏省苏州市高新区实验初级中学练兆明

在一次函数的习题中，常常把两个一次函数图像放置在同一平面直角坐标系中，成为“双直线”图像问题，根据教学经验，不少学生对这类问题常常表现出不适应的倾向.而这类问题又非常“复杂”，既有形式复杂但解法简单的；又有形式简洁但求解较难的；既有涉及平移、对称的变换，又有针对一次函数的“斜率”（一次项系数）、常数“转置”变换的习题等.本文整理近期笔者执教的一节“双一次函数”习题课教学设计，提供研讨.

一、“双一次函数”习题课教学设计

教学活动一：直线的平移变换

（说明：本课例中围绕“直线”的系列问题都是在平面直角坐标系xOy中展开探究的，为了节省篇幅，这个条件不再一一描述）

问题1：将直线y＝x向上平移1个单位，所得直线的解析式是______；

问题2：将直线y＝x向下平移2个单位，所得直线的解析式是______；

问题3：将直线y＝-x向右平移1个单位，所得直线的解析式是______；

问题4：将直线y＝-x向左平移2个单位，所得直线的解析式是______.

设计意图：通4个平移问题引导学生复习直线平移前后的对应关系，即平移方向、单位的关系.特别是后两种平移（左、右）比前两种平移（上、下）要复杂，建议学生认真演算，教学时还可跟进举例，如y＝3x向左（或右）平移2个单位后，所得到的直线解析式是什么？

变式再练1：把直线y＝2x向上平移后得到直线AB，直线AB经过（1，0），求直线AB的解析式.

变式再练2：把直线y＝2x向右平移1个单位后得到直线AB，求直线AB与两条坐标轴围成的三角形面积.

教学活动二：直线的翻折变换

问题5：将直线y＝x+1沿x轴翻折后，所得直线的解析式是________；

问题6：将直线y＝x+1沿y轴翻折后，所得直线的解析式是________；

问题7：将直线y＝-2x+b沿x轴翻折后，所得直线的解析式是________；

问题8：将直线y＝kx+b沿y轴翻折后，所得直线的解析式是________.

设计意图：针对上述4个翻折问题，通过师生对话或追问，可以梳理出直线关于x轴、y轴翻折后对应的直线解析式与原解析式之间的系数变化规律.

变式再练3：将直线y＝-2x+3沿y轴翻折后，所得直线的解析式是________.

变式再练4：若直线y＝2x+2沿x轴翻折后，所得直线与原直线及y轴围成的面积是多少？

教学活动三：一次函数系数的转置变换

问题9：若直线y＝2x+n与y轴的正半轴相交，则直线y＝nx+2x经过哪几个象限？

问题10：两条直线y＝mx+n与y＝nx+m在同一直角坐标系中的位置可能是图1中的（）.

图1

设计意图：通过问题9先安排一个系数为常数，再过渡到问题10中两个参数的转置思考.

变式再练5：图2中各函数图像不可能是一次函数y＝ax-（a-2）图像的是（）.

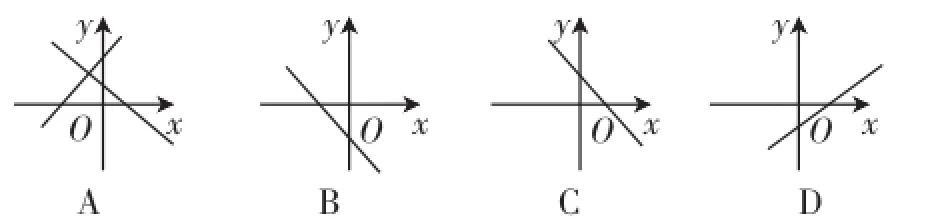
图2

变式再练6：两条直线y＝ax+b与y＝abx（a，b为常数，且ab≠0）在同一平面直角坐标系中的可能情况是图3中的（）.

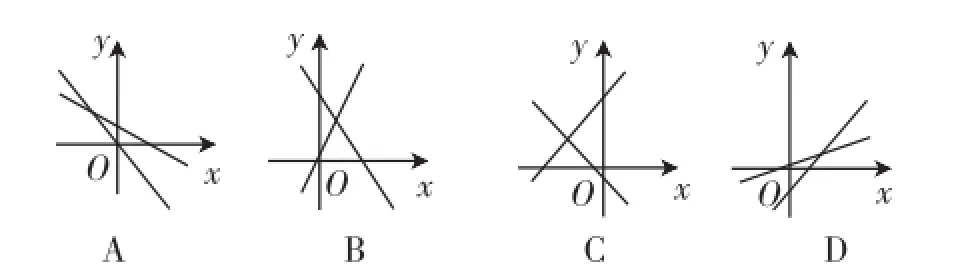
图3

教学活动四：“双一次函数”的拓展研究

问题11：已知直线l1：y＝-2x+4与直线l2：y＝0.5x-2.

（1）在同一平面直角坐标系内，画出这两条直线；

（2）求这两条直线的交点坐标；

（3）根据图像回答，当x在什么范围内取值时，直线l1在直线l2的上方；

（4）求证：l1⊥l2.

问题12：填表并观察下列两个函数的变化情况.

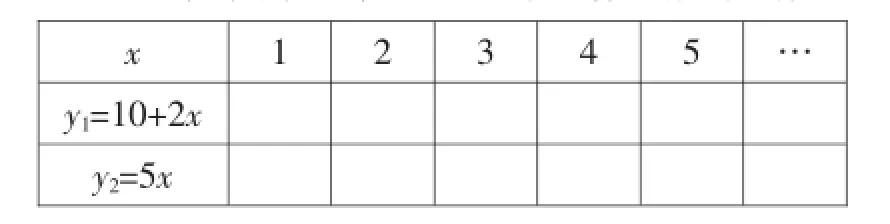
x 1 2 3 4 5…y1＝10+2x y2＝5x

（1）在同一个直角坐标系中画出这两个函数的图像，比较它们有什么不同；

（2）预测哪一个函数值先到2016？

（3）设直线x＝a与（1）中两个函数的图像y1＝10+2x、y2＝5x分别交于点M、N.

①当点M在点N上方时，请指出a的取值范围；

②当MN＝20时，求a的值.

预设讲评：第（1）问是开放式问题，通过学生小组内交流后再汇报各自的观点，并追问有没有不同的思考，将这个问题的成果扩大.

第（2）问，如图4，从函数的图像可知函数y2＝5x的函数值先到2016.这里最好让学生指出两条直线的交点，再从交点的意义解读哪条直线的y值先到2016，更加直观好懂.

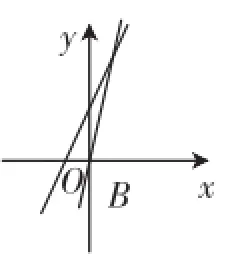
图4

第（3）问主要是训练数形结合思想方法在这类双一次函数问题中的运用.

教学活动五：课堂小结与听课检测

听课检测题：（5个小题，每小题20分，共100分）

在同一平面直角坐标系中，直线l1： y＝-2x与l2：的图像如图5所示.

（1）将直线l1向上平移_____个单位后得到的直线经过点（0，1）；

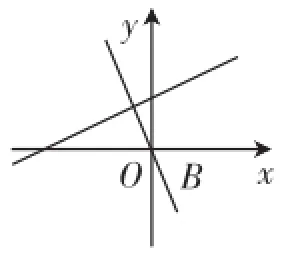
图5

（2）直接写出直线l2关于x轴对称的直线解析式；

（3）当直线l1在直线l2上方时，求出相应的自变量x的取值范围；

（4）若直线l3：y＝（m-4）x-2与直线l2的交点在第一象限，试分析直线y＝-2x+m-3经过哪几个象限；

（5）设直线y＝n与l1、l2分别交于点M、N，当MN＝5时，求a的值.

二、教学立意的进一步阐释

1.预设系列问题串，驱动课堂教学进程

从上面提供的课例来看，我们设计了大量的问题串，意图通过上述系列问题串驱动课堂教学进程.这些问题串又分成几个不同的版块或主题，在每一个主题下的问题串聚焦于一个专题，如教学活动一中我们主要关注的是直线平移的问题，活动二中的4个问题串主要训练的是直线关于坐标轴翻折的问题.上述两个活动中系列问题让学生复习了两条直线的位置与待定系数之间的关系，也为后续问题的深入研究奠定了基础.

2.倡导对话与生成，追求开放数学教学

当下倡导的“以学生为主体”、“以学为中心”的课堂教学，根本上说需要教师功在课前、前置思考和精心预设，包括预设追问、点评，在课堂教学时注意通过恰时恰点的问题促进师生、生生之间的对话与精彩生成，这些努力事实上也是追求所谓的“开放的数学教学”（郑毓信语）.比如，在问题12中，我们设计了“预测哪一个函数值先到2016”就是一个开放式问题，学生的解答和阐释的方式可能会有很多，判断的结果并不重要，重在追问学生预测的理由和依据，如果学生的数形结合思想足够深刻，则可能有非常简洁有力的解释.

3.注重关联式变式，举一反三式的训练

据我们的教学观摩所见，不少同行的习题课往往是选题零乱，缺少主题聚焦.事实上，这也是我们设计上述课例的主要追求，即追求不同问题串之间的关联式变式，并且及时跟进“变式再练”，通过举一反三式的训练帮助学生理解、巩固方法.一直到课堂检测环节，仍然是回顾全课所学内容，再次简单改编数据、字母，以每小题20分的方式反馈听课效果，从我们的教学经验来看，这种跟进检测的教学方式“制造”了必要的紧张氛围，对于目前大班额（50名学生或以上）教学现状来看，提高教学效率有着现实意义.

三、结束语

习题教学在目前中学数学课堂教学中占据很大的比重，是不得不面对的一种课型，然而这方面的课型研究（主要是相关的教学设计）还不丰富，也没有得到应有的重视，我们以一节习题课的设计梳理成文，抛砖引玉，期待批判指正.

1.雍亚波.运算更高效，题型更丰富，思考更深入——以“乘法公式的再认识”习题课教学为例［J］.中学数学（下），2015（11）.

2.刘东升.关联性：一个值得重视的研究领域［J］.中学数学（下），2013（12）.

3.夏建明.一类值得重视的代数运算应用题［J］.中学数学（下），2015（11）.

4.仇锦华.从数学整体观看单元教学［J］.中学数学教学参考（中），2015（11）.H