回归课本.预设变式.构思关联---二次根式章末复习课教学与思考

江苏省如皋市吴窑初级中学　石明建

回归课本.预设变式.构思关联
---二次根式章末复习课教学与思考

《中学数学》(下)近来发表了多篇章末复习课的文章,不少教师对于复习课的教学目标、训练重点、不同教学环节之间的关联、如何回归教材等探讨非常深刻,笔者深受启发,恰好近期有机会执教一次公开课,就选择了二次根式章末复习课开展研讨.本文记录该课的教学流程,并跟进阐释设计意图,与更多同行分享交流.

一、二次根式章末复习课概述

1.客从何处来

引入:乘方运算是我们接触的第5种运算,逆过来思考,就是开方运算,比如,解方程:(1)x2=2;(2)x2=4; (3)x2=8.

变式思考:解关于x的方程:(4)x2=a2+b2;(5)x2=a-3.

同类练习:当x是怎样的实数时,下列各式在实数范围内有意义?

2.性质与化简

(1)复习二次根式性质.

(2)复习两个概念:最简二次根式、同类二次根式.

过渡:在前面的学习中,我们知道二次根式都要化为最简形式,就是要追求最简二次根式的化简目标,请辨析下面一些二次根式,哪些是最简二次根式?

教学预设:第②③④都不是最简二次根式,接下来安排学生化简这些二次根式,顺便要求学生讲清算理,复习二次根式乘法、除法法则.化简之后学生容易得出:.这里进一步追问这些最简二次根式能否合并?为什么?(因为它们都是同类二次根式)接着出示一组合并同类二次根式的练习:①计算:②计算:

3.运算与求值

过渡:在黑板上为学生梳理出本章学习结构图,如图1,为进一步复习二次根式混合运算提供知识框架.

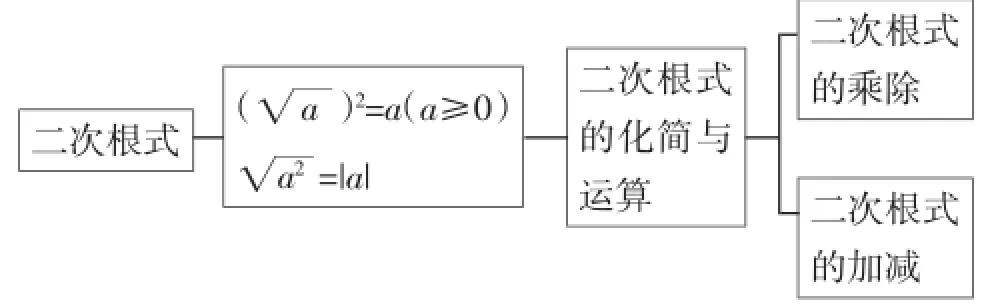
图1

教学预设:学生独立练习前面3个小题没有什么困难,然而第④问是有困难的,事实上根据分母有理化,有

,也就是说,第④问可以转化为第③问求解,在这里是想通过恰当的变式给学生渗透或补充教材上删减的一种分母有理化.根据教学经验,有三分之二的学生能接触到这种分母有理化,补充该内容是必须的,因为这种分母有理化的变形能力是高中可持续学习的必要技能.

(2)代数式求值题:

的值.

教学预设:对第①题追问两组变式问题,(i)当a=1, b=0,c=-8时,求值;(ii)当a=1,b=0,c=-6时,求值(这组值会导致不好求代数式的值,培养学生的批判精神);第②题,可以变式让学生思考,比如的值";第③题不少学生都会"死算",只有少数学生发现从而运用平方差公式简化运算,这里需要重点讲评.

4.情境应用题

(1)如图2,从一个大正方形中截去面积为15cm2和24cm2的两个小正方形,求留下部分的面积.

(2)座钟摆动一个来回所需的时间称为一个周期,计算公式为T=,其中T表示周期(单位:s), l表示摆长(单位:m),g为重力加速度且g=9.8m/s2.假如某座钟的摆长为0.5m,它每摆动一个来回发出一次滴答声,那么在1min内,该座钟发出多少次滴答声?

预设意图:通过两道情境应用问题训练二次根式的列式与化简技能,同时也考验学生的阅读理解能力.

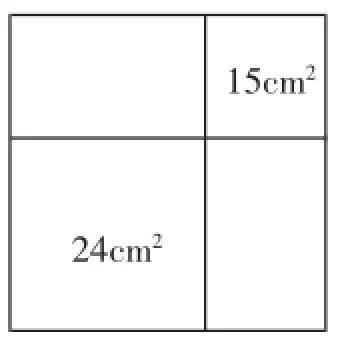
图2

二、教学立意的进一步阐释

1.回归课本,重视双基训练

就笔者所见,有些复习课是来自各地中考试题拼凑起来的习题单,设计两三组例题,然后是同类练习,利用复习课引导学生进行知识复习与巩固的教学设计还不多见,这不能不说是一件憾事.所以我们在上面的课例中,例习题或过渡的引例大多选自教材上的内容,且没有偏题怪题,加强"双基"训练.这事实上也是复习课应该重视的一个选题方向,即对于章末复习课来说,例习题的选择不应追求过分的标新立异,主体上应该尊重和贴近教材例习题的风格,让更多的学生都能过关,达到巩固双基的教学目标.

2.预设变式,加强追问对话

众所周知,经由顾泠沅教授等人的研究,变式教学已成为中国"双基"教学的重要特色.特别是,很多教师感兴趣的则是对习题的变式研究,这突出表现在各类中学数学教学期刊上对习题的改编或命题研究,还包括各级考试(甚至不少地区的中考)的试题呈现,多是一些经典例习题的简单改编与变式.出于上述认知,迫于学生"应试"的眼前利益,复习上加强例习题的变式教学是必要的.然而追求一些较高层次、较隐蔽的变式角度是值得精心构思的,比如,我们在上面"代数式求值"教学环节,将三个习题进行了变式与追问,不仅让学生再次确认解法步骤,同时还可通过追问与对话,引导学生从不同角度理解这类习题,促进学生达到较深刻的解题理解.

3.构思关联,深刻理解数学

本课的开课阶段,我们没有简单地复习二次根式的相关概念,而是选用了学生熟悉的"数学现实",从几道简单的一元二次方程出发,通过乘方、开方逆运算的关系,引出二次根式的意义问题,并在复习进程中,又把一元二次方程的"求根公式"融入代数式求值中,这些都是基于我们对二次根式这一章内容在初中代数中的地位的深刻认识,因为二次根式源自数的开方,下接一元二次方程,通过复习课中不同环节中一元二次方程相关内容的渗透,让学生提前感知一元二次方程,为后续学习奠定必要的心理准备.

1.雍亚波.运算更高效,题型更丰富,思考更深入---以"乘法公式的再认识"习题课教学为例[J].中学数学(下),2015(11).

2.刘东升.关联性:一个值得重视的研究领域[J].中学数学(下),2013(12).

3.夏建明.一类值得重视的代数运算应用题[J].中学数学(下),2015(11).

4.仇锦华.从数学整体观看单元教学[J].中学数学教学参考(中),2015(11).