一次"单元教学"的实践与思考---以"等腰三角形的性质与判定"为例

江苏省如皋外国语学校　刘建

一次"单元教学"的实践与思考
---以"等腰三角形的性质与判定"为例

一、写在前面

去年暑假有幸聆听到著名特级教师李庾南利用单元教学法上的课,给笔者以强烈震撼,为深入了解单元教学法,笔者多次聆听李老师的相关讲座,阅读李老师的相关著作,对单元教学法有了一定的认识.

单元教学,就是在教学过程中,根据知识发生的规律、内在的联系、学生学习的基础、学生可以达到的高度,将学材进行有机整合,分成知识模块,编排成学习单元,教者对学习单元进行整体谋划,安排教学内容,分课时实施,实现单元整体推进的一种课堂教学方式.单元教学有效遏制了知识的碎片化倾向,能有效帮助学生构建知识体系,实现了将单个知识点的重复演练转化为知识块的整体推进和知识体系的综合运用.

鉴于单元教学法的诸多优越性,结合所教学生的实际情况,开学后,笔者尝试对所教内容进行重组,实施单元教学,并在学校数学组内开设研究课,得到组内同仁的肯定.现将所开设研究课人教版八年级上册13.3.1等腰三角形这一单元的教学设计与大家分享.

二、课例展示

(一)目标设计

本单元位于教材中第75至79页,共分两课时进行教学,第1课时与学生一起研究等腰三角形的定义、性质与判定,得出等腰三角形的知识方法体系,第2课时通过一些例、习题的教学对上述知识方法进行巩固提高,以下

1.汤志良.步步有据:推导幂的运算性质---李庾南老师"幂的运算性质"课例赏析[J].中学数学(下), 2015(5).

2.钟启泉.新旧教学的分水岭[J].基础教育课程(上),2014(2).

3.李庾南.自学.议论.引导教学论[M].北京:人民教育出版社,2013.

4.仇锦华.从数学整体观看单元教学[J].中学数学教学参考(中),2015(11).是这一单元的教学目标.

(1)通过经历等腰三角形的性质与判定的探究,建构等腰三角形知识方法体系,丰富从事数学活动的经验和体验;

(2)通过等腰三角形的性质与判定的应用练习,使学生体悟知识的应用价值,激发学生学习的自觉能动性,进一步培养逻辑思维能力和推理论证能力.

(二)教学流程

1.复习旧知,明确研究方向、方法

首先向学生提出以下两个问题.

(1)你能回忆出三角形的哪些知识?想一想我们是从哪些角度研究三角形的?

(2)我们刚刚学过全等三角形、角的平分线、线段的垂直平分线,联系这些内容想一想,研究几何图形一般要研究哪些方面?

设计说明:对于第一问,引导学生可从边、角、重要线段三个角度叙述.对于第二问,让学生再次明确几何图形一般从定义、性质、判定三方面进行研究.从而确定本节课的研究方向、方法:从定义、性质、判定三个方面,选取边、角、重要线段等角度对等腰三角形进行研究.

2.探究新知,构建知识方法体系

(1)定义的复习与深化.

第一步:复习.让学生说出等腰三角形的定义,并分析它与三角形的关系.

第二步:深化.让学生体会定义起着性质和判定双方面的作用,并用符号语言和文字语言表示.

设计说明:等腰三角形的定义学生小学时就学过,八年级继续学习时,首先,要明确它与三角形的从属关系,为将所学新知纳入原有知识系统做准备;其次,应该提出更高的要求,明确定义起着性质和判定双方面的作用,并能用符号语言和文字语言分别表达.

(2)性质的猜想与证明.

第一步:猜想.让学生通过观察、度量、画图、折纸等手段,从边、角、三种重要线段等角度研究等腰三角形的性质,并作出合理的猜想.在教师的帮助下,学生归纳出以下两点性质.

性质1:等腰三角形的两个底角相等.

性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.

设计说明:每个学生的水平不一样,但都可以通过独立探究获得不同程度的认识.这时可通过小组学习提高认识,纠正错误,自我完善.

第二步:证明.

在性质1的证明教学中,教师注意引导两点:一是让学生用多种证法证明,并总结证明过程中的思想方法;二是将定理用文字语言叙述.

在性质2的证明教学中,要注意引导三点:一是通过尝试说出性质2等价命题的方法找到性质2的证明思路;二是根据以上分析,一方面得到定理的简写,即三线合一,另一方面得出定理的符号语言(见图1);三是引导学生接着上面的证明得出等腰三角形的轴对称性,并说出对称轴.

设计说明:性质1证明后关键要从几种证法中总结出共同的数学方法:通过作辅助线构造全等三角形.将性质2换一种说法可以说是文字语言之间的互译;对照图形语言,可将文字语言转化为符号语言;而给出定理的简写语言是对定理深刻理解后的归宿.

(3)判定的获取与证明.

第一步:获取.带领学生分析定义的两个符号语言之间的关系,引导学生分析可以将性质的题设和结论交换,即通过制作逆命题的方法来研究判定,这样共得4个推理(见板书).

第二步:证明.教师从以下两个方面引导:一是让学生通过举反例的方法体会一个命题正确其逆命题不一定正确,从而体会证明的必要性;二是通过"三线合一"与其逆命题的对比,进一步明确"三线合一"性质的特征.

设计说明:有了性质作为基础,研究判定可以采用制作逆命题的方法进行,从而使得判定的研究内容非常明确,关键是体会证明的必要性.将三线合一的三种符号语言及其逆命题的三种符号语言全部放在一起进行比较,让学生明确三线合一性质一定要以等腰作为前提.

(4)形成知识方法体系.

该步骤不是独立的,而是贯穿于刚才三个步骤中.在前三个步骤中利用框图的形式板书,逐渐形成下面的等腰三角形知识方法体系(如图1).

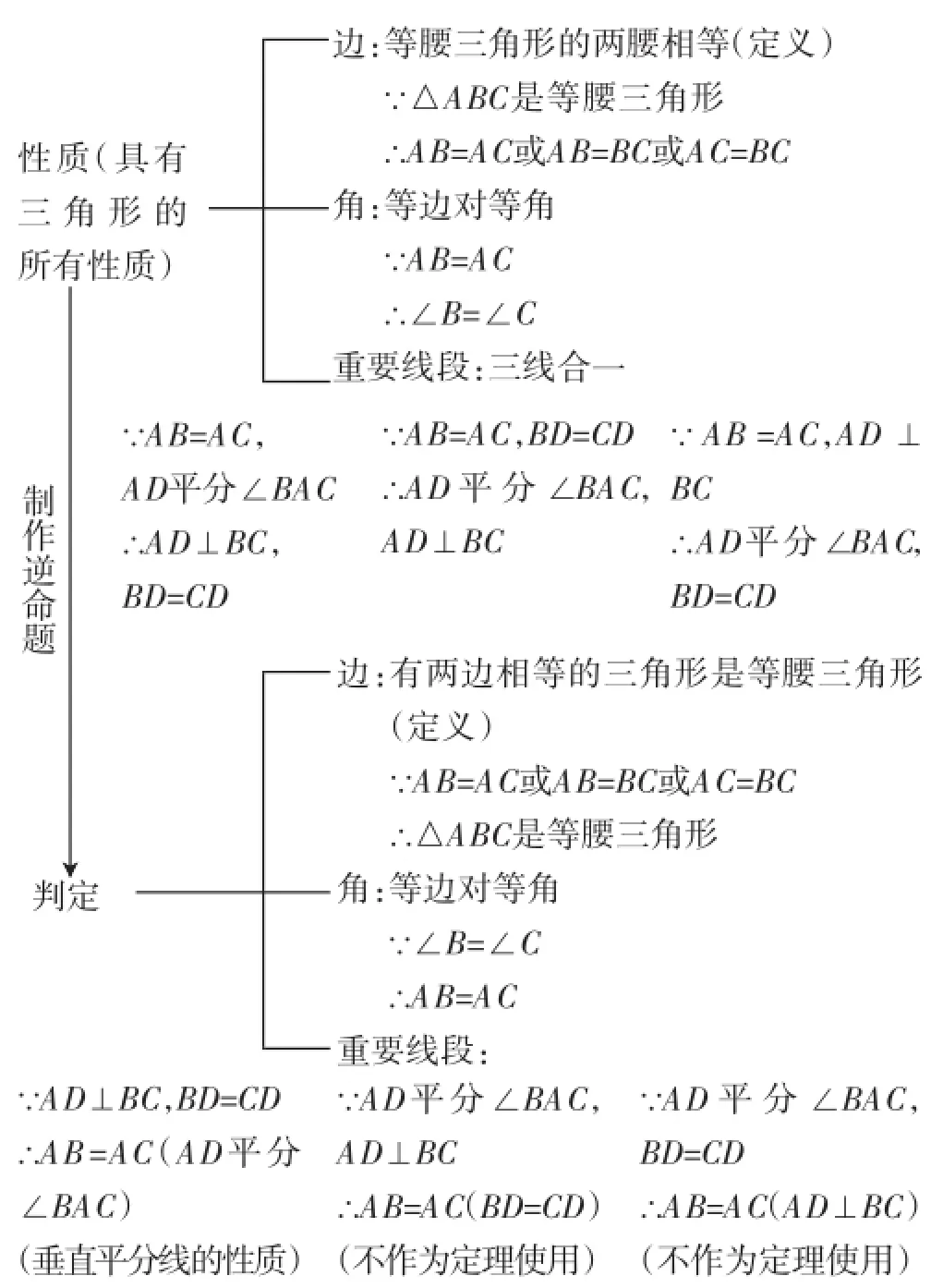
图1

设计说明:随着教学的逐步推进,等腰三角形的知识方法体系逐渐呈现,利用结构图将整节课的脉络呈现出来,有利于学生整体把握这一块知识,学生所获得的不是孤立的、零散的、彼此失去联系的知识,而是层次清晰、彼此相连的知识方法系统.

3.总结提炼,承前启后优化结构

让学生对照上述知识方法体系,总结提炼本节课的数学知识和数学思想方法,并纳入原有知识结构,最后与学生一起展望新知学习(特殊的等腰三角形、四边形,框图中用虚线表示),激起学生继续学习的兴趣,从而将本节课的知识与前后知识联系起来,利用幻灯片投影下面的结构图.

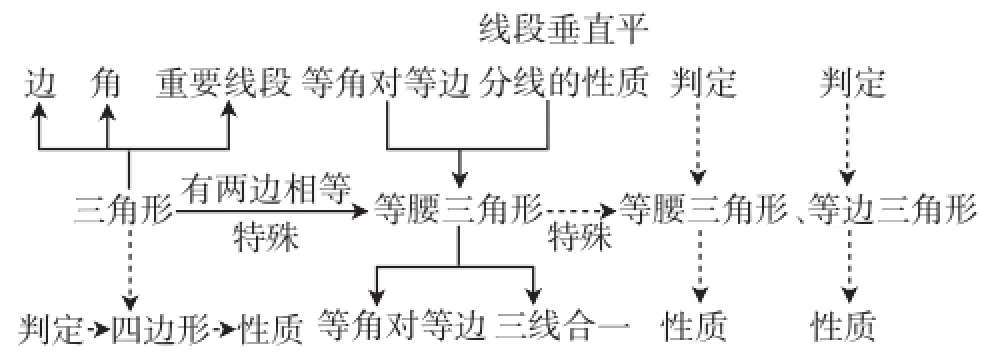
图2

设计说明:图2将本节内容与前后知识进行联系,将所学知识置于更为广阔的数学学习中,对学生的后续学习产生较强的启发作用,对学生学习兴趣的激发和探究欲望的调动也大有作用,从而使学生自主探究成为可能,自学能力逐步增强.

三、教学反思

1.单元教学有利于学生认知结构的优化

等腰三角形这一单元,第1课时研究性质、判定及它们之间的联系,第2课时着重练、议性质与判定的运用.这样做既有助于学生知识结构的整体形成,同时也有利于学生对性质、判定运用方法的整体把握.在本节课中,无论是旧知的复习、定义的教学,还是性质、判定的研究角度,判定的获取都着力于帮助学生构建层次清晰的认知结构,并把所学新知纳入原有认知结构.而对新知的展望,使学生的认知结构得以向前拓展,进一步调整、完善与优化,尽管还是模糊的.而小步子教学不能让学生体会知识间微妙深邃的联系,所学知识是碎片化的.

2.单元教学有利于学生自学能力的培养

本节课中通过旧知的复习,让学生明确研究新知的方向、方法:从定义、性质、判定三个方面,选取边、角、重要线段等角度对等腰三角形进行研究.而这一研究方法是普适的,对于接下来学习特殊的等腰三角形、四边形等有很强的导向作用.同样,通过制作逆命题的方法由性质研究判定无疑也具有普适性.这样做,学生获得的不只是等腰三角形的有关知识和方法,更重要的是获取到了程序性和策略性知识.可见,单元教学十分注重知识间的内在的本质的联系,并有效地利用这一联系使学生的自学能力培养成为可能.

3.单元教学对教师提出了更高的要求

作为教师,必须以课程标准为标准,以教材为参照,以学生的实际情况为依据,以学生的最大发展为旨归,真正做到"用教材教",而不是"教教材".教师要深刻把握知识间的内在联系,找准每一个知识的"根",即知识的生长点,再将它们有机串联起来.所以单元教学在给学生提供更大的发展空间的同时,也对教师提出了更高的要求.

参考文献:

1.章建跃.全面深化数学课改的几个关键[J].课程.教材.教法,2015,35(5).

2.钟启泉.新旧教学的分水岭[J].基础教育课程(上),2014(2).

3.李庾南.自学.议论.引导教学论[M].北京:人民教育出版社,2013.