模糊数学评价法在食品感官评价中的应用

李玉珍，肖怀秋*

（湖南化工职业技术学院制药与生物工程学院，湖南株洲412000）

模糊数学评价法在食品感官评价中的应用

李玉珍，肖怀秋*

（湖南化工职业技术学院制药与生物工程学院，湖南株洲412000）

模糊数学综合评价法能通过模糊数学的隶属度和隶属函数理论，将影响感官质量的多因素间关系进行数学抽象化并建立理想化评价模式，其最大优点是可以实现相对复杂且不够确定因素影响的数学化，但也存在计算复杂，权重域矢量确定有很强主观性以及当评价指标隶属度权系数偏小时易出现评价模糊，分辨率变差，甚至评判失效等不足。该文论述了模糊评价基本原理、构建步骤及其应用等，并指出了模糊数学在感官评价中的优势与不足，同时对模糊数学评价法的应用进行了展望，如适当降低感官评定论域、适当增加感官评判员数量和将模糊评价法与其他非线性处理优化方法联用等。

食品感官评价；模糊数学；评定域；隶属函数

食品感官评价是指食品感官评价者通过视、听、嗅、味和触觉等感知渠道对食品感官评价属性做出综合评价的系统分析方法［1-2］。在实际中，由于感官评价属性界限有一定模糊性，无法定量评价，易受到感官评价者主观因素的干扰。模糊数学综合评价法是基于模糊数学中隶属度与隶属函数理论对影响食品感官质量的多因素间关系进行数学抽象化并建立反映其本质属性和动态影响过程的理想化评价模式，实现影响因素的定量化，从而对被评价对象隶属等级进行综合评价［3］。模糊数学综合评价结果的客观性和准确性受评价体系的构建、评价数据的可靠性及权重域等影响，但由于能很好地减少感官评价指标间及感官评价主体间的主观评定误差，提高了评价结果的科学性、合理性和客观性，且评定过程可基于计算机程序自动完成，在食品感官评定中广泛应用［4-7］。近些年，模糊数学综合评价法在食品感官评价中的应用限于具体方法的运用，对理论体系的介绍较为鲜见，制约了模糊数学综合评价方法的推广与应用。本文从模糊数学综合评价法的基本原理、步骤及其在食品感官综合评价中的应用等方面进行了系统综述，并对模糊数学综合评价法的应用进行了展望，以期为模糊数学综合评价法应用起到一定的推动作用。

1　模糊数学评价法的基本原理及构建步骤

1.1模糊数学评价法的基本原理

模糊数学综合评价法根据模糊数学的隶属度和隶属函数理论把定性评价转化为定量评价，即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。由于感官评价属性界限具有模糊性，无法实现感官评价指标的定量描述，易受感官评价主体的影响，而模糊数学通过构建影响食品感官质量的多因素与评价指标的数学关系来表征影响规律并建立理想化的评价模型，从而实现评价指标的数字化，进而实现评价指标等级的综合评定，可减少评价主体间的主观评定误差［8］。模糊综合评判方法最大优点是通过精确的数字手段将相对复杂、不够确定的多因素问题转化为有数据依据的简单易行的定量的评价模式，具有很好的客观性。而且模糊评价结果为矢量，而非具体点值，蕴含信息更加丰富，既可有效评价评定对象，还可获得更多的参考信息。其缺点是由于模糊综合评价法计算相对复杂，对权重域矢量的确定有较强的主观性，当感官评定论域较宽时，特别在权矢量和为1的条件约束下，各评价指标相对隶属度权系数往往偏小，容易出现权矢量与模糊矩阵R不匹配，甚至导致超模糊现象，分辨率变差，隶属度高低的区分效力降低，甚至造成评判失效［5，9］。

1.2模糊数学评价法的构建步骤

模糊数学评价法构建步骤如图1所示。

图1　模糊数学评价法构建流程Fig.1 Establishment of flow chart o f fuzzy mathematical evaluation method

1.2.1确定感官评定论域

感官评定论域是指最能反应该食品感官质量的一组评价指标的集合［1］，表示为U=｛u1，u2，…，un｝，如胡璇等［10］在利用模糊数学综合评价法对剁椒进行感官评价指标时构建了U=｛色泽u1，脆性u2，香气u3，滋味u4｝的感官评定论域。

1.2.2确定感官评定评语论域

评语论域是参评者对评价指标反馈信息的集合，即确定需要评定的等级，可用文字、具体数值或等级表示［11-12］。记为V=｛v1，v2，…，vn｝，v表示对应的评价等级或分数。宋亚琼等［13］采用模糊数学综合评价法对臭鳜鱼进行感官评价时，构建了V=｛优秀v1，良好v2，一般v3，较差v4｝的感官评定评语论域。

1.2.3确定权重域及评价指标隶属函数

感官评价时，各感官评价指标赋予的权重直接影响模糊评价结果，权重分配方案的正确与否直接影响到评价结果的科学性、正确性和客观性。根据各指标权重值确定权重域矩阵A=（a1，a2，…，an），其中a1，a2，…，an［ai∈（0，1）］是各评价指标相应的隶属度，且满足条件（a1+a2+…+an）=1。建立评价指标集U对评价集的隶属函数使根据隶属函数计算得到的隶属度值的大小与该项指标在综合评价中的重要性相适应。隶属函数为单调函数，隶属度rmn在0～1之间（m=1，2，…，m；n=1，2，…，n）。隶属度计算公式如下：

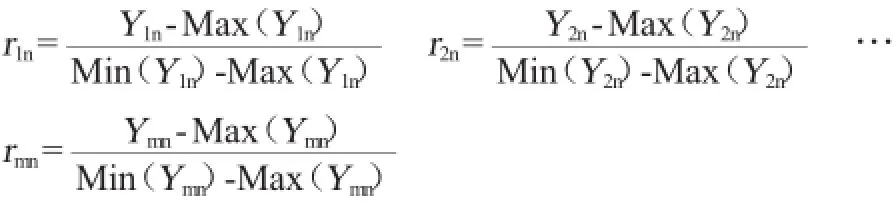
1.2.4确定模糊评判矩阵

模糊评判矩阵即参加模糊综合评判各因素根据相应隶属度所组成的评判结果矩阵R，定义为：

1.2.5模糊综合评价值的计算

为了对模糊综合评价值进行计算，在评价集中引入模糊子集Y（也称为评价集）。由模糊评判矩阵R与权重域矩阵A通过模糊变换可得到，表示为Y=A×R=｛b1，b2，…，bm｝［13］。过程如下：

1.2.6模糊综合评判

根据模糊综合评判数学模型原理计算综合隶属度，得到欲评定产品感官质量综合评判的结果向量，对食品感官评价进行综合评定。

2　模糊数学评价法在食品感官评价中的应用

吴靖娜等［14］以新鲜鲍鱼为原料，通过构建｛色泽，风味，质地｝的评定论域和｛很差，差，一般，较好，很好｝的评语集，通过单因素试验和响应面优化的技术联用研究了浸泡温度、浸泡时间、烘干温度和烘干时间对熏鲍制品感官指标的影响，获得了优化的液熏鲍生产工艺。张娜等［15］以感官评定为基础研究了蒸制时间、油炸温度、油炸时间对香酥鸡块感官品质的影响，构建了｛色泽，气味，滋味，组织状态｝的评定论域和｛优秀，一般，较差｝的评语论域的评价矩阵，利用正交试验优化了香酥鸡块的制作工艺。殷建忠等［16］以｛色泽，香气，滋味，典型性｝为感官评定论域，构建以｛很好，较好，一般，较差，差｝为评语论域的单因素评价矩阵，在正交试验基础上，基于模糊综合评判法对紫甘薯色素废渣发酵酒工艺影响因素进行综合评价，评判结果准确、科学。肖玫等［17］将正交设计与模糊数学评判综合运用于葡萄酒的配方研制中，有效地解决了评酒师感官评定中各种指标的评分差异和品评员之间评价结果差异的复杂问题。黄六斌等［18］以｛色泽，香气，口味，风味｝构建感官评定论域，并构建柑桔酒感官评定模糊矩阵，对感官评定结果做归一化处理后，应用模糊数学综合评价法对柑桔酒感官影响指标进行优化分析，获得了优化生产工艺参数，评定结果更具有客观合理性。徐慧诠等［19］以制备的菠萝果汁粉末油脂为原料，添加乳粉、白砂糖及柠檬酸制备新型菠萝果乳固体饮料，构建了U=｛色泽，香气，口味，综合质量｝的感官评定论域和V=｛优等，良好，中等，较差，劣｝的感官评定评语论域，并根据各感官评定指标的重要性赋予权重，在正交试验基础上结合模糊数学综合评定法对制备工艺进行了优化分析，获得了优化配方。刘静波等［20］以红松松针为原料，在正交试验基础上，通过构建以｛色泽，气味，口感，外观｝为评价指标的评定论域和以｛优，良，中，差｝为评价等级的评语论域，采用二元对比法对评定论域的评价指标赋权，构建了红松针茶饮料的模糊数学矩阵并优化了红松针茶饮料的制备工艺。梁治军等［21］为优化燕麦牛奶复合蛋白饮料的配方，确定了感官评定论域U=｛色泽，香味，口感，状态｝和感官评定评语论域V=｛优，良，中，差｝，根据各评价因素重要性赋权并构建权重向量A，通过正交试验结合模糊数学评价获得了优化的生产配方。为了提高模糊评价法的识别效率，可以将模糊评价法与其他非线性处理优化方法联用［4］。如田广文等［22］在单因素试验基础上采用中心组合响应面法对风味型酸乳最佳配方进行了优化分析并获得满意结果。谭祥峰等［23］将均匀设计与模糊数学综合评价法联用确定了最优香菇菌汤配方。宋亚琼等［13］用Box-Behnken响应面优化法并结合模糊数学综合评价方法对臭鳜鱼发酵工艺进行优化分析并确定了臭鳜鱼发酵最佳方案。刘美迎等［24］运用模糊数学和聚类分析对2013年陕西渭北地区的14个鲜食葡萄品种的品质进行模糊数学综合评价，实现了葡萄综合品质全面和客观的评价。此外，也可以将模糊数学与非线性处理特性的人工神经网络相结合进行食品风味的评价［25-26］。

3　展望

由于模糊综合评价法计算相对复杂，对权重域矢量的确定有较强的主观性，当感官评定论域较宽时，特别在权矢量和为1的条件约束下，各评价指标相对隶属度权系数往往偏小，容易出现权矢量与模糊矩阵R不匹配，甚至导致超模糊现象，分辨率变差，隶属度高低的区分效力降低，甚至造成评判失效［27］。因此，为了提高模糊综合评价法的分辨率，在不影响感官评定结果准确性的条件下适当降低感官评定论域［7］。由于感官评判员的主观评判对评分影响较大，因此在感官评定过程中，宜适当增加评判员的数量，消除或减少主观评定因素的影响，增加评判结果的可信度［28］。此外，也可考虑将模糊评价法与其他非线性处理优化方法联用提高模糊数学综合评价效果，多评价方法的优化组合将是食品感官综合评价发展的一个趋势［29-30］。

［1］LAW LESS H T，HEYMANN H.Sensory evaluation of food：princip les and practices［M］.New York：Springer Science&Business Media，2010.

［2］MEILGAARD M C，CARR B T，CIVILLE G V.Sensory evaluation techniques［M］.Boca Raton：CRC press，2006.

［3］PERROT N，IOANNOU I，ALLAIS I，et al.Fuzzy concepts applied to food product quality control：a review［J］.Fuzzy Set Syst，2006，157（9）：1145-1154.

［4］ZOLFAGHARI Z S，MOHEBBI M，NAJARIYAN M.Application of fuzzy linear regression method for sensory evaluation of fried donut［J］. Appl Soft Com put，2014，22：417-423.

［5］BIRLE S M，BECKER H T.Fuzzy logic control and soft sensing applications in food and beverage processes［J］.Food Control，2013，29（1）：254-269.

［6］ZHANG H P.Application on the entropy method for determ ination of weight of evaluating index in fuzzy mathematics for w ine quality assessment［J］.Adv J Food Sci Technol，2015，7（3）：195-198.

［7］DEBJANI C，DAS H.Aggregation of sensory data using fuzzy logic for sensory quality evaluation of food［J］.J Food Sci Technol，2013，50（6）：1088-1096.

［8］魏永义，郭明月，尹军杰，等.模糊数学综合感官评价调味料酒的应用研究［J］.中国调味品，2015，40（10）：52-54.

［9］HUANG S Y，TEGHEM J.Stochastic versus fuzzy approaches to multiobjective mathematical programming under uncertainty［M］.Netherlands：Springer Science&Business Media，2012.

［10］胡璇，夏延斌.基于模糊数学的剁椒感官综合评价方法［J］.食品科学，2011，32（1）：95-98.

［11］HONG H.Fuzzy mathematics study on evaluating food sensual quality［J］.Food Sci，2004（6）：48.

［12］张明，王燕，欧阳梦云.模糊数学感官评价法优化豆渣发酵工艺［J］.中国酿造，2015，34（9）：75-78.

［13］宋亚琼，闫晓明，丁之恩，等.基于模糊数学的臭鳜鱼的感官评定［J］.中国酿造，2015，34（5）：123-126.

［14］吴靖娜，路海霞，蔡水淋，等.基于模糊数学感官评价法优化液熏鲍生产工艺［J］.食品安全质量检测学报2015，6（12）：4932-4941.

［15］张娜，游新侠.基于模糊数学综合评价法的香酥鸡块加工工艺研究［J］.肉类研究，2015（11）：18-20.

［16］殷建忠，王琦，吴少雄，等.正交试验法优化水提紫甘薯色素废渣发酵酒工艺及模糊综合评判模型评价感官质量［J］.食品科学，2011，32（6）：131-134.

［17］肖玫，李毅念，廖海，等.应用模糊数学评判葡萄酒的生产配方［J］.江苏农业科学，2011（3）：350-352.

［18］黄六斌，丁雪梅，穆洪霞，等.模糊数学法在柑桔酒感官品评中的应用［J］.酿酒科技，2014（9）：65-68.

［19］徐慧诠，郑为完，高媛媛.模糊数学在菠萝果乳固体饮料制备中的应用［J］.食品工业科技，2012，33（1）：308-310.

［20］刘静波，吴丽英，宫新统，等.基于模糊数学综合感官评价的红松针茶饮料的制作［J］.现代农业科技，2013（7）：308-311.

［21］梁治军，韩甜甜.模糊数学评判燕麦牛奶复合蛋白饮料的生产配方［J］.饮料工业，2015，18（3）：42-45.

［22］田广文，陈德育，杨祥.灵芝酸乳发酵工艺响应面优化与模糊数学评价［J］.食品工业，2013（3）：15-19.

［23］谭祥峰，于海，葛庆丰，等.基于均匀设计和模糊数学的香菇菌汤制备工艺［J］.食品科学，2012，33（2）：115-118.

［24］刘美迎，李小龙，梁茁，等.基于模糊数学和聚类分析的鲜食葡萄品种综合品质评价［J］.食品科学，2015，36（13）：57-64.

［25］EERIKÄINEN T，LINKO P，LINKO S，et al.Fuzzy logic and neural network applications in food science and technology［J］.Trends Food Sci Technol，1993，4（8）：237-242.

［26］NELLES O.Nonlinear system identification：from classical approaches to neural networks and fuzzy models［M］.Netherlands：Springer Science &Business Media，2013.

［27］HÖHLE U，RODABAUGH S E.Mathematics of fuzzy sets：logic，topology，and measure theory［M］.Netherlands：Springer Science&Business Media，2012.

［28］雷红.模糊数学在食品感官评价质量控制方法中的应用［J］.食品科学，2004，25（6）：185-188.

［29］CHAKRABORTY S，RAO P S，M ISHRA H N.Response surface optimization of process parameters and fuzzy analysis of sensory data of high pressure-temperature treated pineapp le puree［J］.J Food Sci，2015，80（8）：1763-1775.

［30］BANDEMER H W.Fuzzy data analysis［M］.Netherlands：Springer Science&Business Media，2012.

Application of fuzzy mathematics evaluation method in food sensory evaluation

LI Yuzhen，XIAO Huaiqiu*
（Department of Pharmaceutical and Bioengineering，Hunan Vocational Technical College of Chemical and Industrial Technology，Zhuzhou 412000，China）

Fuzzy mathematics evaluation method approach（FMEM）can be used as an evaluation method in food sensory evaluation through establishing idealized evaluation model and abstracting the relationship between the sensory-quality affecting factors based on degree of membership and membership function theory.The greatest advantage for FMEM is to transfer these relatively complex and uncertain factors effect into mathematic equation，but the disadvantages were as complex calculation，very strong subjectivity in determ ination of weight field vector and easily lead to fuzzy evaluation，worse resolution，even evaluation inefficiency.The article summarized the fundamental principle，construction steps and applications in food sensory evaluation，pointed out the advantages and disadvantages，and discussed the application of FMEM in food sensory evaluation，such as properly reduce evaluation domain，and properly increase the number of sensory estimator and the utilization of the combination of FMEM and other nonlinear optimization method.

food sensory evaluation；fuzzy mathematics；evaluation domain；membership function

O159；O 224；X797

0254-5071（2016）05-0016-04

10．11882/j．issn．0254-5071．2016．05．004

2016-01-06

湖南省高校科研项目（12C1049）；国家自然科学基金（31050012）；湖南化工职业技术学院院级项目（HNHY2015002）

李玉珍（1981-），女，讲师，硕士，主要从事蛋白质生物化学方面的教学与研究工作。

肖怀秋（1981-），男，副教授，硕士，主要从事植物蛋白质资源精深加工及功能多肽方面的研究工作。