关于广义正态分布性质的研究

殷清涛（甘肃省敦煌市敦煌中学）

关于广义正态分布性质的研究

殷清涛
（甘肃省敦煌市敦煌中学）

一、引言

正态分布是由德国著名数学家高斯首先得到的，所以也常常称为高斯分布。正态分布在数学、物理、化学及工程中都具有非常重要的地位，尤其在统计学中有着重大的影响力。事实上，正态分布是应用最为广泛的一种分布，它存在于人们生产生活的各个方面。例如，同一机器生产出的大量产品的质量分布；同一年龄段人类的身高、体重分布；某一地区年降水量的分布；科学实验中测量同一物体的误差分布，理想气体的速度分布等等。现在人们知道，正态分布是由中心极限定理保证的。实际应用中，还存在一些其他形式的分布，例如t分布、F分布等，其实，这些分布也是由正态分布直接导出的。正态分布可以用来估计频数分布，制定参考值范围，质量控制等等。然而，我们知道，作为保证正态分布的中心极限定理，是以大数法则为前提的，具体地说，事件的数目越多，中心极限定理越严格，才能保证趋向于正态分布。理论上讲，事件的数目为无穷大时，中心极限定理才严格正确，分布才是正态分布。实际生活中，事件的数目显然不是无穷大，因此正态分布实际上并不能准确无误地表示分布规律。在本篇文章中提出以广义正态分布代替传统正态分布，可以很有效地解决这一矛盾。

二、广义正态分布及其运算法则

传统正态分布的分布函数可表示为：

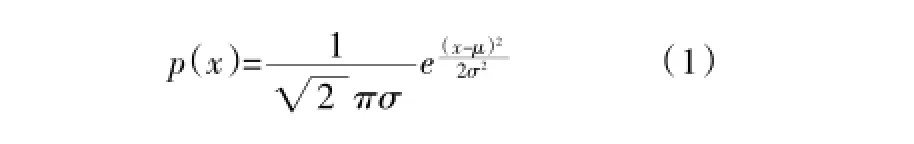
从上式可以看出，正态分布的核心是自然指数e，是自然对数的底数，是一个无限不循环小数，其值约为2.71828……，它是一个超越数。自然指数在整个数学史上都具有非常重要的地位。自然指数是由一个重要极限给出的。即当n趋于无限时（1+1/n）n=e。以自然指数为底数的对数叫做自然对数，一般用ln表示。自然对数的含义是在单位时间内，持续的翻倍增长所能达到的极限值。

所谓广义正态分布，就是在传统的正态分布基础上，增加上一个量q，该量称为非广延参数，已经被广泛应用于物理、化学、生物、工程、经济、计算机科学等各个领域中。它的正确性已经得到了广泛承认。接下来，从微分方程出发研究广义正态分布：

考虑这样一个简单的一阶线性微分方程：dy/dx=y，它的解是y=ex，反函数是y=lnx。很容易看出该微分方程导出了自然指数和自然对数。

再考虑非线性微分方程：dy/dx=yq，它的解是y=［1+（1-q）x］1/（1-q）=exq，反函数是当q无限接近1时，得到了自然指数和自然对数的极限形式，以后简单称之为广义自然指数和广义自然对数。以广义自然指数为基础，便可以得到广义正态分布函数：

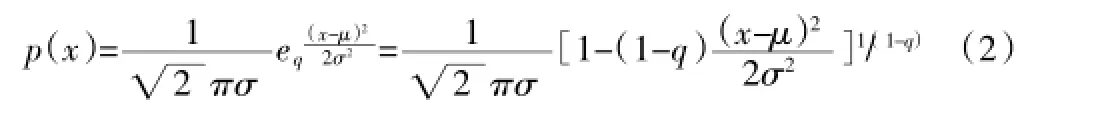
对于自然对数和自然底数，有如下基本性质：

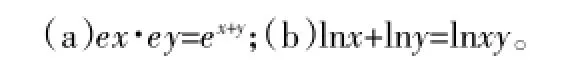
这两个基本性质是正态分布得以广泛应用的一个重要理由，因为它们使得正态分布在运算中极为简便，若缺少这两个基本性质，几乎所有涉及正态分布的运算量都将增大很多倍。然而，广义自然指数与广义自然底数却不具备传统自然对数与传统自然底数的这些优良性质，即exq·eyq=eq（x+y+（1-q）xy），很显然exq·eyq不等于exyq；同理从lnq（xy）=lnqx+lnqy+（1-q）lnqlnqy可以看出当q不等于1时，lnqx+lnqy不等于lnq（xy），这使得广义正态分布在实际应用中计算繁琐，下面定义一套新的运算法则，可以有效简化广义正态分布的计算量。

如果同时定义广义乘法与广义加法规则如下：

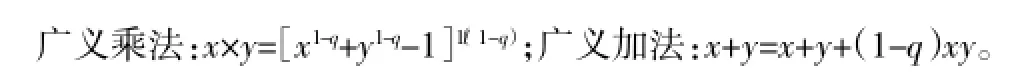
则以上性质可以得到保持：

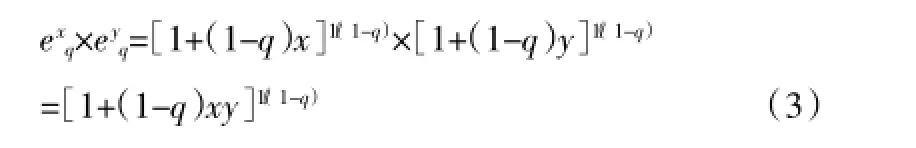
可以看到在广义乘法规则下exq×eyq正好等于ex+yq；

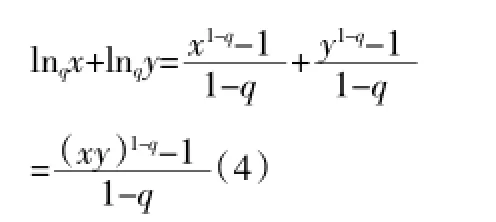
可以看到，在广义加法规则下lnqx+lnqy正好等于lnqxy。

既然定义了广义乘法与广义加法规则，广义除法与广义减法规则也就自然而然地给出，此处不再详述。接下来，在此基础上建立较为复杂的运算：广义微分和广义积分，从而形成一整套广义运算规则。首先定义广义微分：

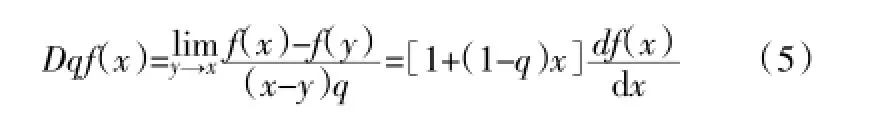
于是相应的广义积分由下式给出：

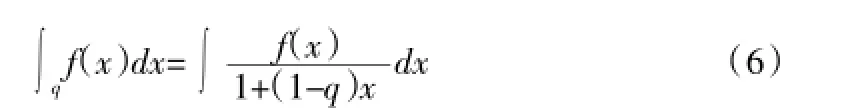
以上讨论的广义正态分布下的运算法则都是相对简洁的，事实上实际运算中还会出现很多本文未能包含的情况，但不管多么复杂的运算，总能从本文定义的加减乘除以及微分积分经过适当的组合以及变形给出。在广义运算规则下，广义正态分布中的运算量大大减少，这很好地减轻了工业生产和科学实验中的计算量，具有非常重要的实际意义。

三、广义正态分布的跨学科应用

为了进一步说明广义正态分布的重要性，以下将举出两个广义正态分布成功应用的例子。

例1.某地抽样调查两百名十九岁的男大学生的身高，发现平均身高为172.5厘米，标准差为3.98厘米。求这两百名十九岁男大学生中，有多少人身高分布在168.5厘米到176.5厘米之间？若依照传统正态分布理论，可以很容易得出67%的男大学生处在该范围，于是算出应该有134人身高分布在168.5厘米到176.5厘米之间。然而实际情况却有所偏差。该地抽样调查结果显示，这两百名十九岁的男大学生身高处在该范围的人数为136人。应用广义正态分布理论，取q值为0.96，可发现广义正态分布计算所得值为136人，与实际抽样调查结果相同。事实上，传统正态分布与实际的偏差来源于抽样的局限性。抽样的样本容量越小，理论与实际的偏差越大，q越偏离1，越应该使用广义正态分布。传统正态分布严格来讲只适用于抽样容量无限大的情况。

例2.理想气体分子的速度分量分布。物理学中经常以理想气体为例来验证新理论的正确性。所谓理想气体，是指气体分子本身体积与容器总体积相比很小，可忽略不计，且气体分子之间的作用力也很小，也可忽略不计的气体。一般认为，理想气体的速度分量遵循麦克斯韦分布律，麦克斯韦分布律实质上也就是正态分布。然而，理想气体的速度分量分布，是否真的遵从正态分布，一般多年来都是作为一个既定的事实，从未在实验上直接测量验证过。近年来，越来越多的科学家认为，正态分布或许只是一种可能的分布，而不是唯一的分布。另外，理想气体的条件过于苛刻，实际上不存在能够满足理想气体条件的真实气体。广义正态分布为对应的广义麦克斯韦分布律提供了一种可能，对于不同的气体，取不同的q值，可以更好地描述真实气体系统。

周秋生.广义正态分布及其二次函数的性质［J］.测绘工程，1999（1）.

·编辑薄跃华