偏对称正态分布的若干性质

□陈超 田芫 宗序平

统计分布的性质是学者们研究的热点，国内外有许多学者研究过偏正态分布，并应用于统计实践。在此基础上，定义了偏对称正态分布，并研究了其性质。此类分布包括偏均匀正态分布，偏t 正态分布，偏拉普拉斯正态分布，偏Logistics 正态分布和偏三角正态分布等，并探讨了它们的一些性质。

引言

国内外有许多学者研究了偏正态分布，如Azzalini[1](1985）定义了偏正态分布的概念；Henze[2](1986)研究了偏正态分布的一些性质；Xie[3](2010)等研究了偏正态非线性回归模型方差参数的齐性检验。这类分布已经得到了广泛的应用，为工程领域中一些分布不对称的数据，提供了更加合理的拟合模型。除此之外，它们还有助于研究模型的鲁棒性，以及作为贝叶斯分布的先验分布。这种模型的构建可参见Azzalini(1985）。对偏正态分布的扩展也已经有了很多研究，如Gupta[4](2002)等构造了偏对称模型；Ferreira[5](2010)等研究了偏尺度混合正态分布的一些性质，以及Labra[6](2012)等研究了混合尺度偏正态分布的参数估计和模型诊断，都得到一些很好的应用。在此基础上，定义了偏对称正态分布，并举出了一些例子，探讨了它们的一些性质。

定义1.1 设随机变量Y 的概率密度函数为f (y)，f (y)为偶函数，Φ(x)是标准正态分布函数，随机变量X 的概率密度函数为

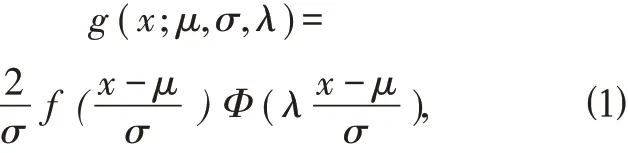
其中λ 为偏度系数(可取任意实数)，μ 是位置参 数，σ 是 尺 度参数，则称X 服从偏对称正态分布。

（i）μ=0,σ=1 时，g(x;λ)=2f (x)Φ(λx)，称X 服从标准偏对称正态分布；

（ii） μ=0,σ=1,λ →+∞ 时 ，g(x;λ)=2f (x)Φ(λx)趋向于 ||Y 的概率密度函数；

（iii）μ=0,σ=1,λ →-∞ 时 ，g(x;λ)=2f (x)Φ(λx) 趋 向 于-|Y|的概率密度函数；

（iv） μ=0,σ=1,λ=0 时 ，g(x;λ)=f (x) 是Y 的 概 率 密 度函数。

性质1.1 设X，Y 是上述定义中的随机变量，则

（i）X 的偶阶距和Y 的偶阶距相同，且于λ 无关。

（ii）X2与Y2有 相 同 的 分 布函数。

证明： 令φX(t)是X 的特征函数，φY(t)是Y 的特征函数，则

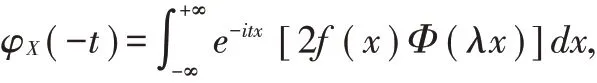
令x=-x，则

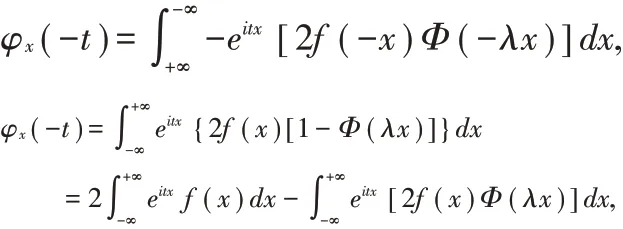
因此，就得到了

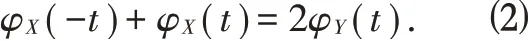
设n 为任意的正整数，(2)式两边对t 求2n 阶导数，有

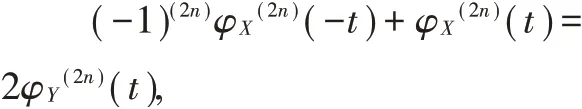
所以，

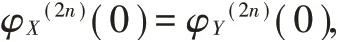
因为，

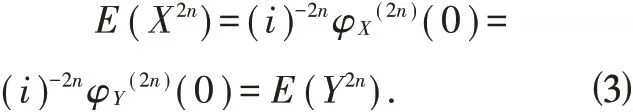
所以，上式与λ 无关所以，第（i）条结论得证。

由(3)式可知，X2与Y2的n 阶距是相同的，所以X2与Y2有相同的分布函数，即性质（ii）成立。

本文将讨论f 取不同的对称概率分布函数的情况。首先取f 为标准正态分布函数，得到了偏正态分布的密度函数，并总结了偏正态分布的若干性质，然后分别取f 为均匀分布，t 分布，Laplace 分布，Logistics 分布，推导出了偏均匀正态分布，偏t 正态分布，偏Laplace 正态分布，偏Logistics 正态分布，并研究了它们的一些性质，最后列举了若干类似的分布，有待进一步的讨论。

若干偏对称正态分布

(1) 偏正态分布

定义2.1 设φ(x)和Φ(x)是标准正态分布的概率密度函数和分布函数，随机变量X 的概率密度函数为

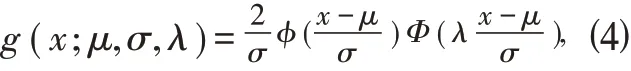
其中λ 是偏度系数(可取任意实数)，μ 是位 置参数，σ 是尺 度参数，则称X 服从偏正态分布。特别的 ， μ=0,σ=1 时 ， g(x;λ)=2φ(x)Φ(λx)，则称X 服从标准偏正态对称分布。图1 给出了λ 取不同值的标准偏正态对称分布的概率密度函数图像。

性质2.1 如果随机变量X 服从标准偏正态对称分布，则X2服从自由度为1 的卡方分布。

性质2.2 如果随机变量X 服从标准偏正态分布，M(t)是X 的距母函数[4]，则

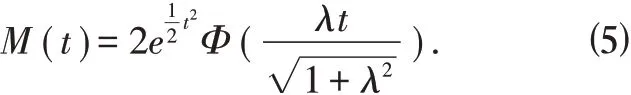
由上述性质，可以求出

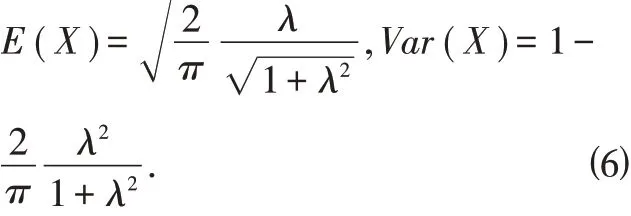
进一步，可以求出

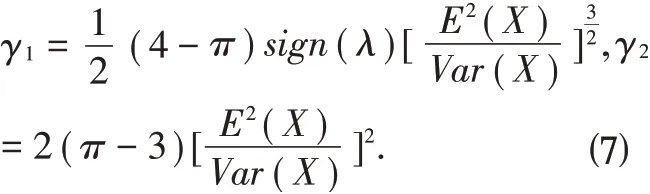
其中，γ1和γ2分别是X 的偏度系数和峰度系数。

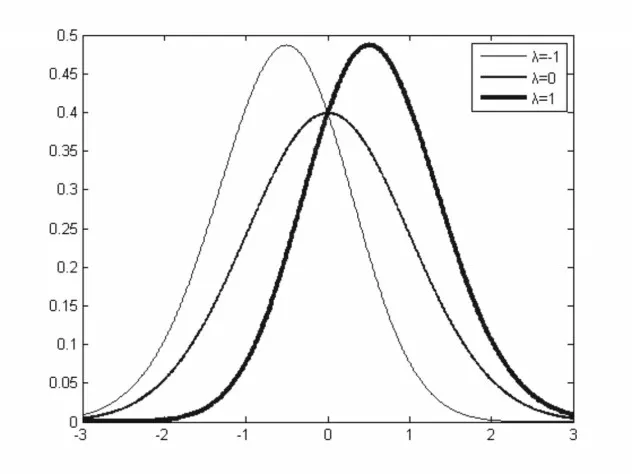
图1 λ 取不同值的标准偏正态对称分布的概率密度函数图

（2）偏均匀正态分布

定义2.2 设均匀分布的密度函数

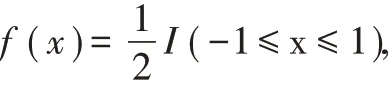
Φ(x)是标准正态分布函数，随机变量X 的概率密度函数为

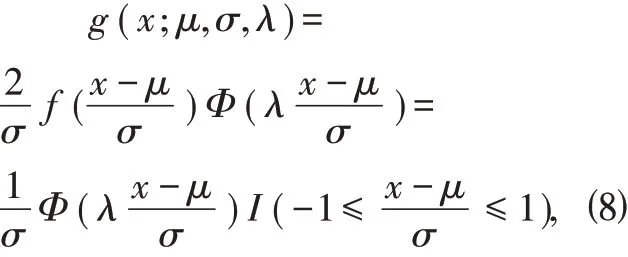
其中λ 是偏度系数(可取任意实数)，μ 是 位置参数，σ 是 尺度参数，则称X 服从偏均匀正态分布。特 别 的，μ=0,σ=1 时，g(x;λ)=Φ(λx)I(-1≤x ≤1)，则称X 服从标准偏均匀正态分布。图2 给出了λ取不同值的标准偏均匀正态分布的概率密度函数图像。

性质2.3 如果随机变量X 服从标准偏均匀正态分布，M(t)是X 的距母函数，则

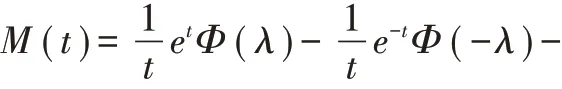
图2 λ 取不同值的标准偏均匀正态分布的概率密度函数图

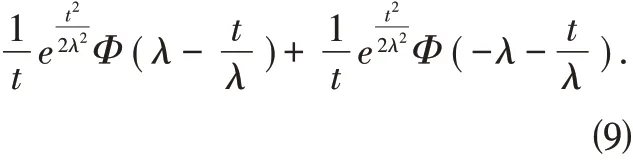
证明：

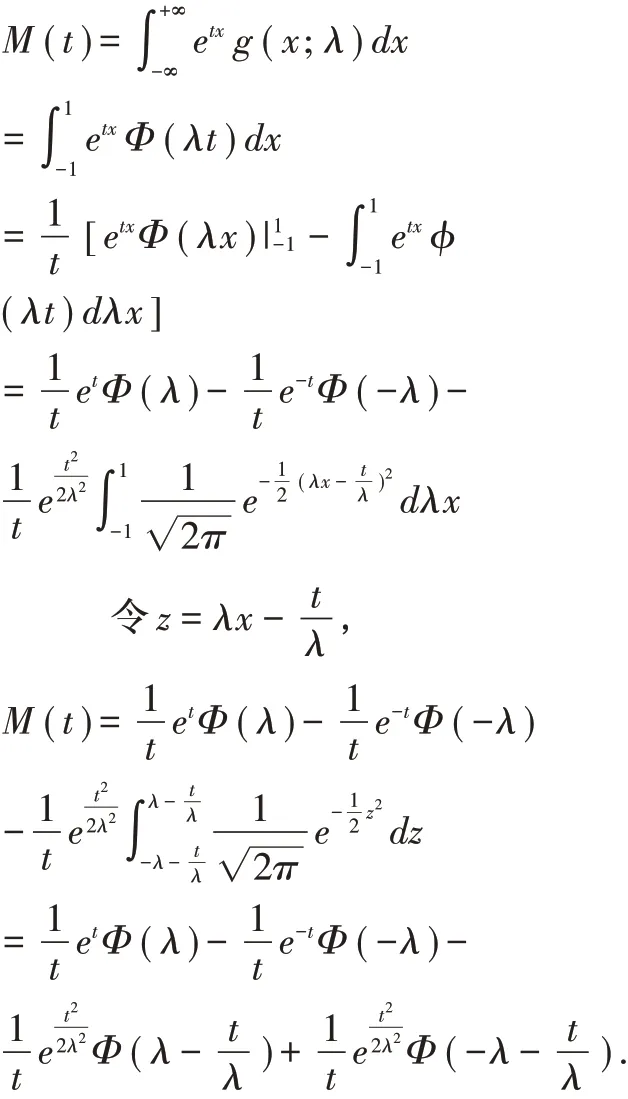
由上述性质，可以求出

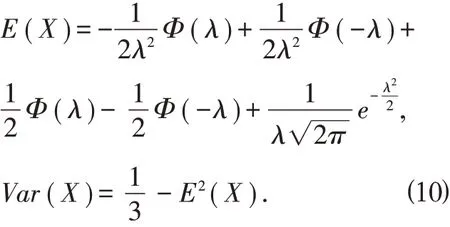
（3）偏t 正态分布

定义2.3 设t 分布的密度函数

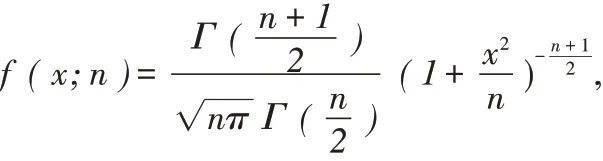
Φ(x)是标准正态分布函数，随机变量X 的概率密度函数为

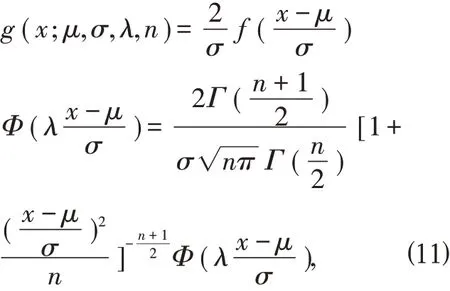
其中λ 是偏度系数(可取任意实数)，n 是自由度，μ 是位置参数，σ 是尺度参数，则称X 服从偏t 正态分 布。 特 别 的，μ=0,σ=1 时，g(x;λ,n)=2f (x;n)Φ(λx)，则称X服从标准偏t 正态分布。图3 给出了n=1 时，λ 取不同值的标准偏t正态分布的概率密度函数图像。

性质2.4 如果随机变量X 服从标准偏t 正态分布，M(t)是X 的距母函数，则

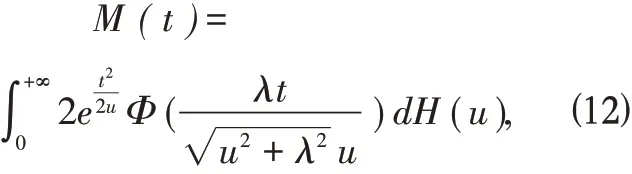
由(11)式可以求出

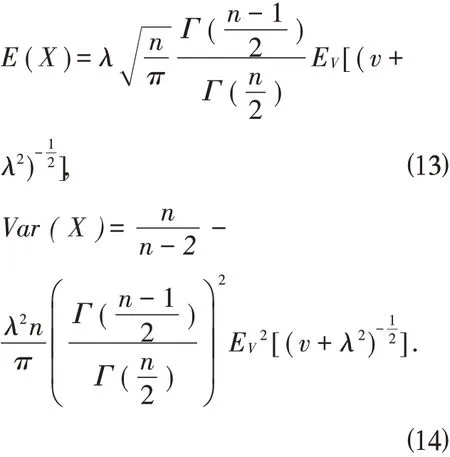
（4）偏Laplace 正态分布

定义2.4 设Laplace 分布的密度函数

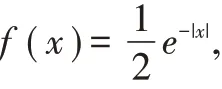
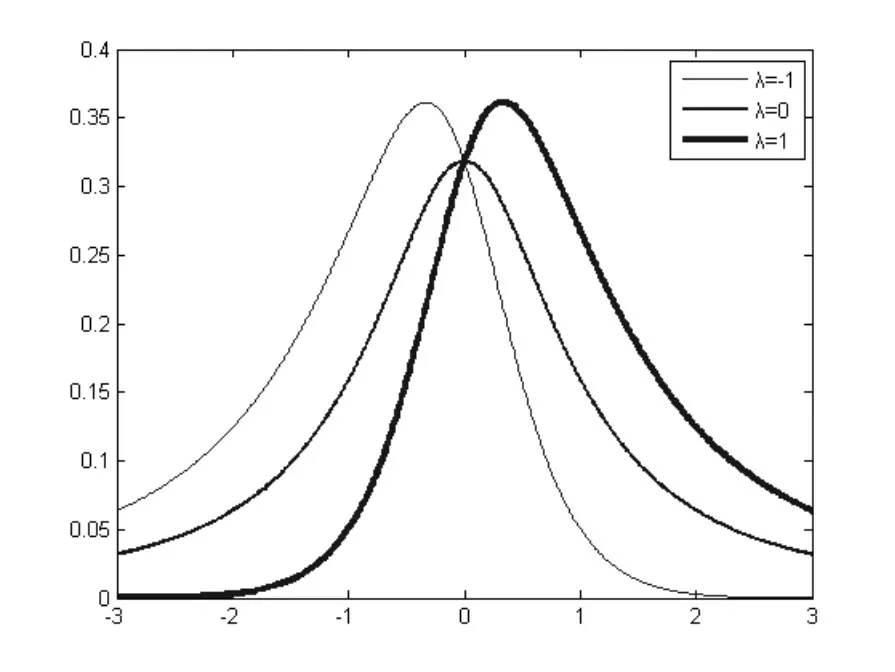
图3 λ 取不同值的标准偏t 正态分布的概率密度函数图

Φ(x)是标准正态分布函数，随机变量X 的概率密度函数为

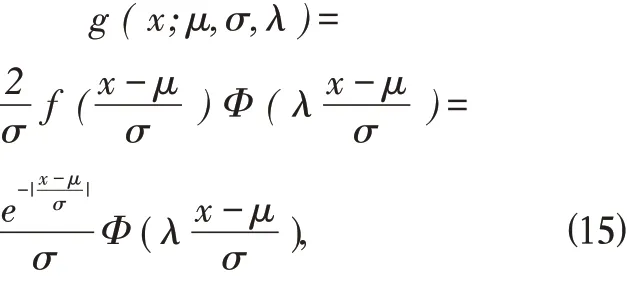
其中λ 是偏度系数(可取任意实数)，μ 是 位置参数，σ 是尺度 参数，则称X 服从偏Laplace 正态分布。 特 别 的，μ=0,σ=1 时，g ( x;λ)=e-|x|Φ(λx)时，称X 服从标准偏Laplace 正态分布。图4 给出了λ 取不同值的标准偏Laplace 正态分布的概率密度函数图像。

性质2.5 若随机变量X 服从标准偏Laplace 正态分布，且偏度系数λ ＞0，M(t)是X 的距母函数，则当-1＜t ＜1 时，

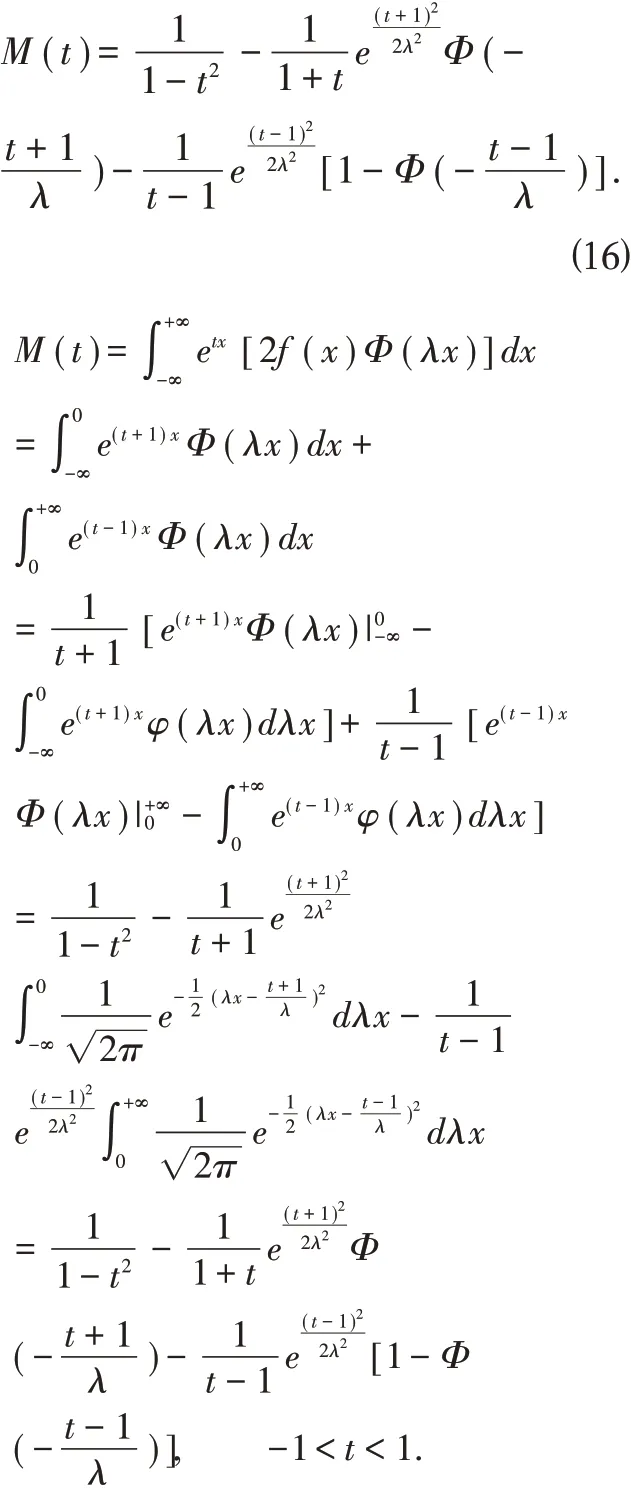
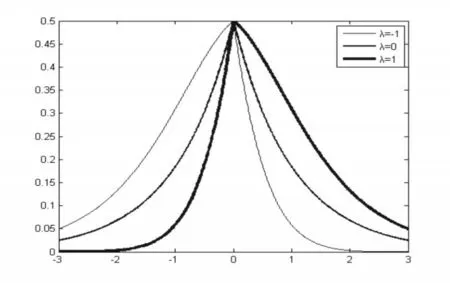
图4 λ 取不同值的标准偏Laplace正态分布的概率密度函数图

由上述性质，可以求出

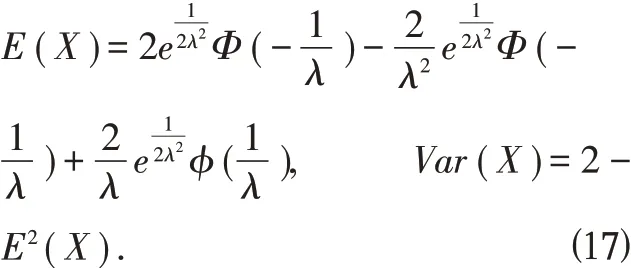
（5）偏Logistic 正态分布

定义2.5 设Logistic 分布的密度函数

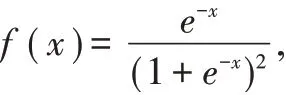
Φ(x)是标准正态分布函数，随机变量X 的概率密度函数为

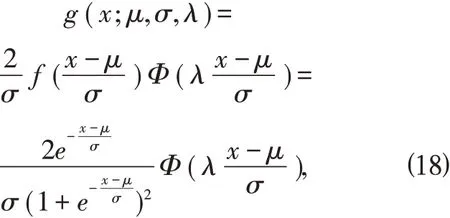
其中λ 是偏度系数(可取任意实数)，μ 是位置参数，σ 是尺度 参数，则称X 服从偏Logistic 正态分布。 特 别 的，μ=0,σ=1 时，g(x;λ)=2f (x)Φ(λx)，则称X 服从标准偏Logistic 正态分布。图5 给出了λ 取不同值的标准偏Logistic正态分布的概率密度函数图像。

性质2.6 如果随机变量X 服从标准偏Logistic 正态分布，X2概率密度函数为fX2(t) 则

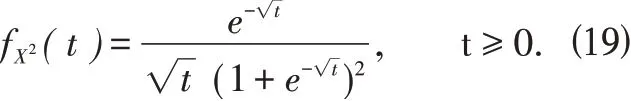
由(19)式可以求出

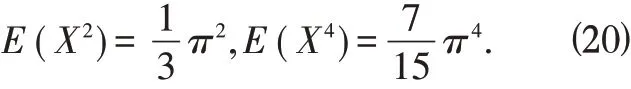
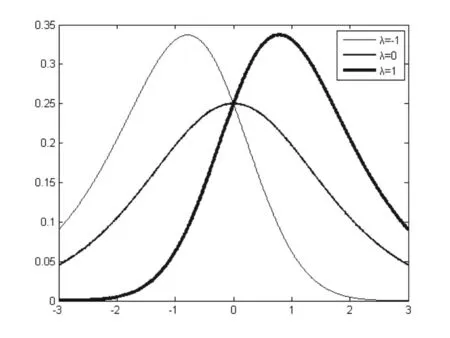
图5 λ 取不同值的标准偏Logistic正态分布的概率密度函数图

（6）偏三角正态分布

定义2.6 设三角(Triangular)分布的密度函数

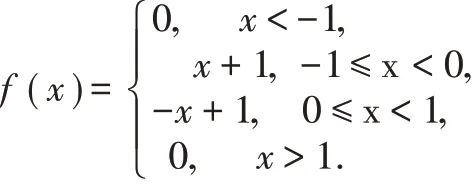
Φ(x)是标准正态分布函数，随机变量X 的概率密度函数为

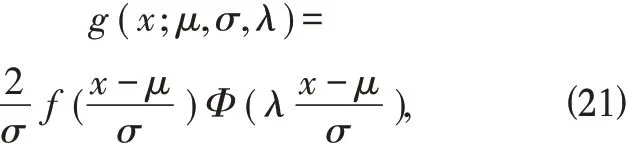
其中λ 是偏度系数(可取任意实数)，μ 是位置参 数，σ 是 尺 度参数，则称X 服从偏三角正态分布。特 别 的，μ=0,σ=1 时，g(x;λ)=2f (x)Φ(λx)，则称X 服从标准偏三角正态分布。图6 给出了λ 取不同值的标准偏三角正态分布的概率密度函数图像。

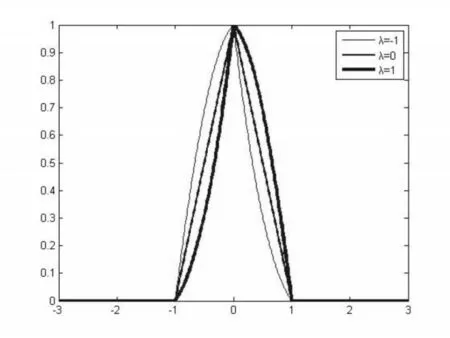
图6 λ 取不同值的标准偏三角正态分布的概率密度函数图

性质2.7 如果随机变量X 服从标准偏三角正态分布，E(X) 和Var(X)是X 的数学期望和方差，则

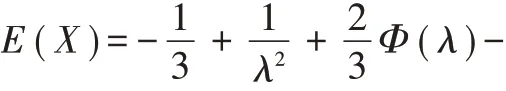
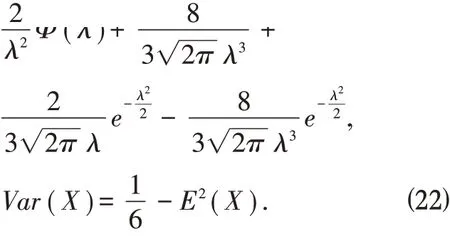
其他相关分布

Φ(x)是标准正态分布函数，随机变量X 的概率密度函数为

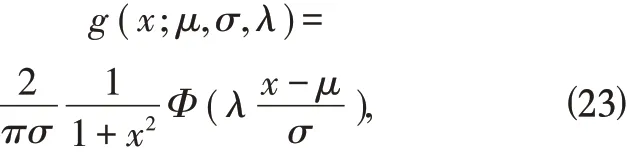
其中λ 是偏度系数(可取任意实数)，μ 是位置参 数，σ 是 尺 度参数，则称X 服从偏Cauchy 正态分布。 特 别 的，μ=0,σ=1 时，g(x;λ)=2f (x)Φ(λx)，则称X 服从标准偏Cauchy 正态分布。

定义3.2 设Slash分布的密度函数

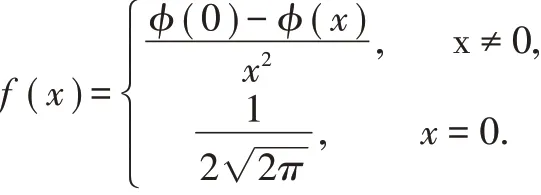
φ(x)和Φ(x)是标准正态分布的概率密度函数和分布函数，随机变量X 的概率密度函数为

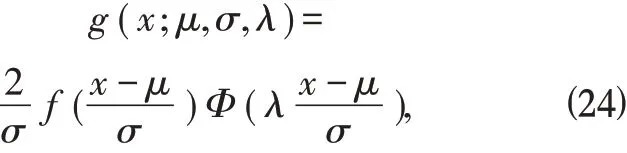
其中λ 是偏度系数(可取任意实数)，μ 是位置参 数，σ 是 尺 度参数，则称X 服从偏Slash 正态分布。特 别 的，μ=0,σ=1 时，g(x;λ)=2f (x)Φ(λx)，则 称X 服 从 标 准 偏Slash 正态分布。

本文在偏正态分布的基础上进行了扩展，研究了一类带有偏度系数的概率密度函数，定义了偏对称正态分布，并举出了一些例子，为分布不对称的数据提供了一种新型的拟合模型。这对于回归分析方面的应用是有意义的。进一步，可以通过EM，ECM[7]，ECME[8]等算法研究偏对称正态分布模型参数估计方面的问题，也可以通过Score 检验、Ward 检验对模型参数的齐性进行诊断，也可以对模型参数的显著性进行研究，这方面的工作会在以后的研究中继续进行。