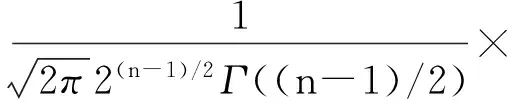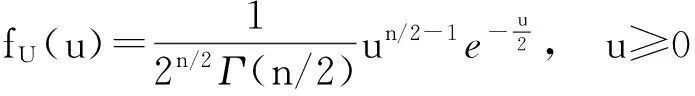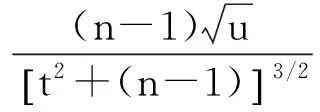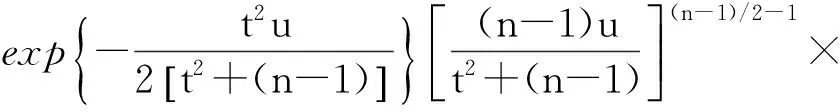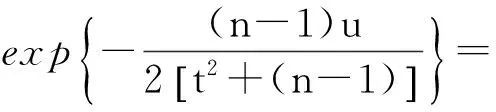关于两参数Birnbaum-Saunders疲劳寿命分布统计分析的2个注记

徐晓岭, 王蓉华, 顾蓓青*

(1.上海对外经贸大学 统计与信息学院,上海 201620； 2.上海师范大学 数理学院,上海 200234)



关于两参数Birnbaum-Saunders疲劳寿命分布统计分析的2个注记

徐晓岭1, 王蓉华2, 顾蓓青1*

(1.上海对外经贸大学 统计与信息学院,上海 201620； 2.上海师范大学 数理学院,上海 200234)

通过Monte-Carlo模拟说明目前用于求解两参数Birnbaum-Saunders疲劳寿命分布尺度参数的2种方法可能无法得到尺度参数的区间估计.进一步指出，在利用广义枢轴量法给出尺度参数以及参数函数的置信区间过程中存在错误,并用反例进行了说明,同时给出了正确的证明.

两参数Birnbaum-Saunders疲劳寿命分布；尺度参数；区间估计；广义枢轴量

Journal of Zhejiang University(Science Edition), 2016,43(5):539-544

Birnbaum-Saunders模型是概率物理方法中的重要失效分布模型,由BIRNBAUM和SAUDERS于1969年在研究主因裂纹扩展导致的材料失效过程中推导而来,其后广泛应用于机械产品的可靠性研究,在电子产品性能退化失效分析中也有重要应用.

设T服从两参数Birnbaum-Saunders疲劳寿命分布BS(α,β),其分布函数F(t)与密度函数f(t)分别为：

其中,α>0称为形状参数,β>0称为尺度参数,φ(x),Φ(x)分别为标准正态分布的密度函数与分布函数,即

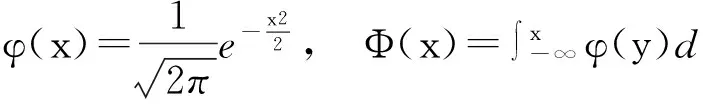
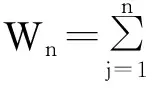
假设Yj是独立同分布的非负随机变量,均值为μ,方差为σ2,当然这个假设只在某些应用中成立.设失效发生在第s个周期,即在第s个周期Wn首次超过临界值w,易见

P(s≤n)=P(Wn≥w).

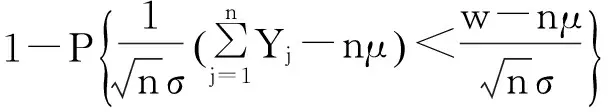
当n很大时,由中心极限定理知：

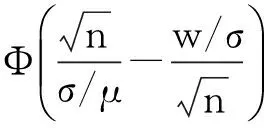
由于存在多周期,每一周期持续时间都很短,可以用连续时间t(失效需要的时间)来替换离散时间n,故相应的累积分布函数F(t)为

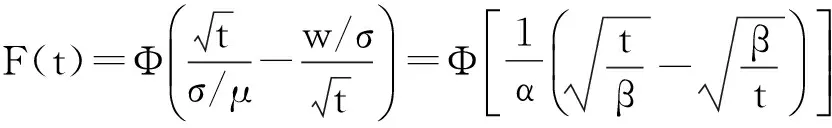
其中,

由于Birnbaum-Saunders疲劳寿命分布是从疲劳过程的基本特征出发,其分布比常用寿命分布如威布尔分布、对数正态分布更适合描述某些因疲劳失效产品的寿命分布规律.此分布已成为可靠性统计分析的常用分布之一.

关于两参数Birnbaum-Saunders疲劳寿命分布BS(α,β)的统计分析已有较多研究.BIRNBAUM等[1]结合背景分析提出了BS疲劳寿命分布,DESMOND[2]基于生物模型给出了更加通用的推导,进一步说明BS疲劳寿命分布使用的物理缘由,放宽了文献[1]中所给出的最初的假设条件.DESMOND[3]研究了BS分布与逆高斯分布的关系,指出用此分布来描述产品的疲劳寿命较其他分布更合理.BIRNBAUM等[4]讨论了全样本场合下参数的极大似然估计.ENGELHARDT等[5]应用蒙特卡罗方法和MLE的渐进正态性讨论了参数置信区间估计以及形状参数和尺度参数的假设检验问题.RIECK等[6]研究了将疲劳寿命分布的对数线性模型用于加速寿命试验,此模型还可用于比较平均寿命,同时进一步研究了MLE与最小二乘估计,并用大样本方法给出了参数的近似区间估计和假设检验方法.虽然BS分布参数的极大似然估计有很多优点,但非线性方程较为复杂,无法直接求解,而常规的矩估计不一定存在或唯一,NG[7]给出了修改矩估计的方法.DUPUIS等[8]给出了参数的ROBUST估计.CHANG等[9]给出了可靠度函数的区间估计.RIECK[10]针对对称截尾样本,给出了BS分布的参数估计.OWEN和PADGETT在文献[11-13]中给出了BS分布可靠度的贝叶斯估计并研究了幂律加速寿命试验模型.KUNDO等[14]讨论了BS分布的失效率函数的形状,得到该失效率函数是一个倒浴盆函数.

在国内,较早研究BS分布的有王炳兴等[15],文献[15]讨论了BS疲劳寿命分布及其对数线性模型的参数估计问题,给出了BS疲劳寿命分布中参数的逆矩估计方法,此方法计算简单，且对可能异常点相对稳健,并用实例说明该估计方法的可行性；文献[16]研究了定数截尾和定时截尾场合下的参数点估计与区间估计.王蓉华等[17]在双边定数截尾场合下, 给出了BS分布参数的拟最小二乘估计和近似极大似然估计, 并用随机模拟方法比较了极大似然估计、近似极大似然估计和拟最小二乘估计的偏性和均方误差；文献[18]还研究了定数截尾场合下BS分布参数的近似极大似然估计；文献[19]研究了缺失数据场合下BS分布尺度参数的区间估计.孙祝岭[20]研究了BS分布参数的区间估计问题,提出用新的枢轴量来构造尺度参数的经典置信区间,此方法具有较为简单的显式表达式，应用回归分析给出了BS分布参数的最小二乘估计和形状参数区间估计方法.用计算机随机模拟了区间估计的效果,结果显示效果非常好[21].孙祝岭[22]给出了BS分布变异系数的区间估计和假设检验方法.在失效机理保持不变的条件下,还讨论了BS分布环境因子的估计问题[23].王炳兴[24]研究了形状参数以及均值、分位数、可靠度等可靠性指标的广义区间估计.牛翠珍等[25]利用文献[24]中的广义枢轴量法对分布在不同参数情形下的BS进行了比较.周磊等[26]提出了一种基于BS分布的互连线时延模型,避免了查表运算,且仅需要采用前2个瞬态,计算简单,准确性较好,同时提出了一种精度修正算法,修正后该方法具有更好的适应性,90纳米工艺TCAD仿真实验表明,该模型在效率、精度、难易程度等方面具有一定的优势.赵建印等[27]利用BS分布对布朗运动、几何布朗运动和Gamma过程等随机过程退化轨道建立了形式统一的加速退化模型,并采用极大似然方法估计模型参数.最后针对某自控温伴热电缆,利用所建模型进行加速退化分析,有效验证了模型的正确性和合理性.

关于两参数Birnbaum-Saunders疲劳寿命分布尺度参数的区间估计通常采用文献[19-20]所提出的方法,本文通过MonteCarlo模拟说明这2种方法有可能无法得到尺度参数的区间估计.同时指出文献[24]在利用广义枢轴量法给出尺度参数以及参数函数的置信区间过程中存在错误,用反例进行了说明,并给出了正确的证明.

1　关于尺度参数β的区间估计的一个注记

1.1文献[19]方法研究

设总体T～BS(α,β),T1,T2,…,Tn为来自总体T的一个容量为n的简单随机样本,其次序统计量记为T(1)≤T(2)≤…≤T(n).

则Z(1)≤Z(2)≤…≤Z(n)与样本量为n标准正态分布N(0,1)的前n个次序统计量同分布.

令

即G(β)为枢轴量,其分布与参数无关.由文献[19]知，G(β)对β严格单调递减,将G(β)作如下恒等变换：

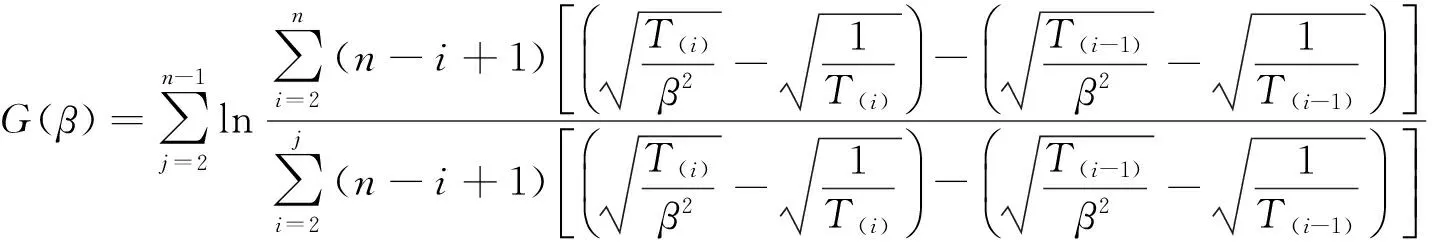
则

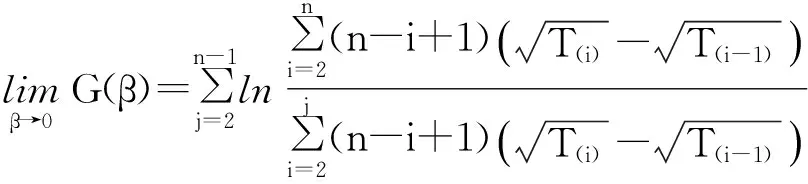
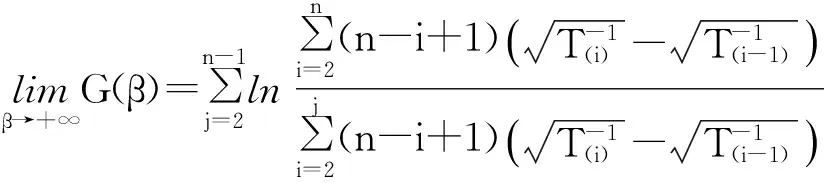
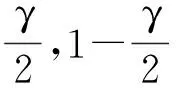
1.2文献[20]方法研究

设T1,T2,…,Tn为来自Birnbaum-Saunders疲劳寿命分布总体T～BS(α,β)的一个容量为n的简单随机样本,其样本观察值为t1,t2,…,tn.

令

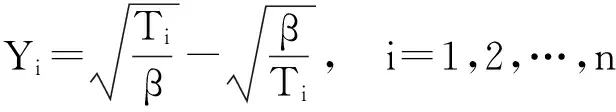
则

Yi～N(0,α2),i=1,2,…,n.

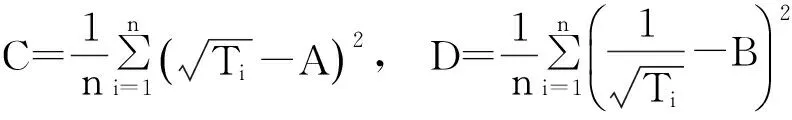
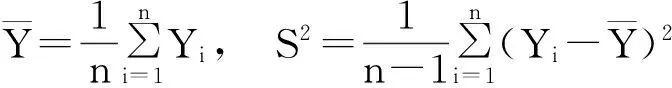
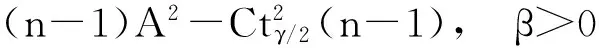
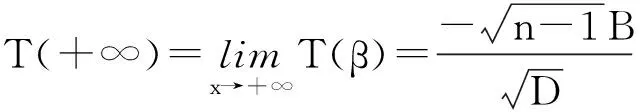
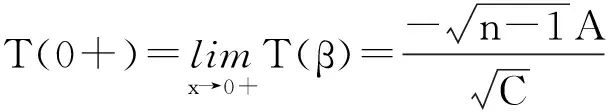
因此对于样本,若

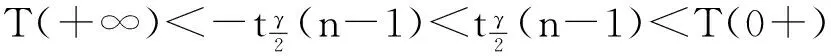
则有双侧置信区间；

若为下列3种情况之一：

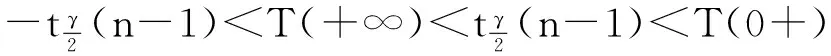
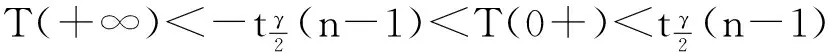
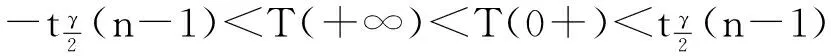
则有没有双侧置信区间.

为弥补文献[20]的不足,需解决尺度参数β的区间估计问题，这将另文讨论.

2　关于广义置信区间的一个注记

设T1,T2,…,Tn为来自两参数Birnbaum-Saunders疲劳寿命分布总体T～BS(α,β)的一个容量为n的简单随机样本,其次序观察值为t1,t2,…,tn.

令

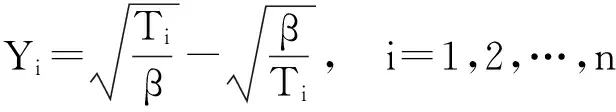
则

Yi～N(0,α2),i=1,2,…,n.

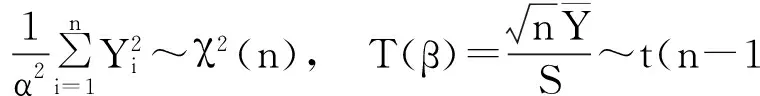
据文献[24],

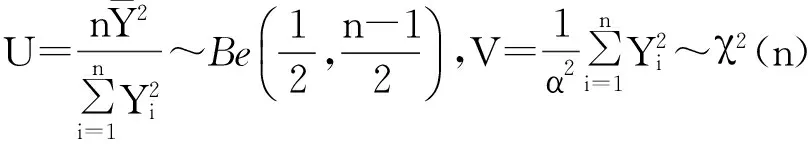
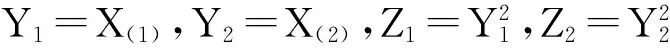
下证“T(β)与V相互独立”.

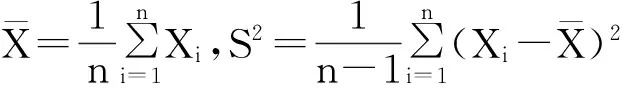
证明不失一般性，可假设σ=1.易见

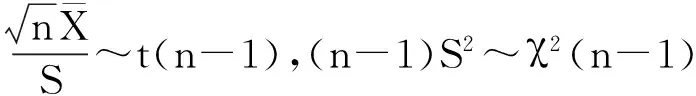
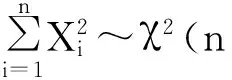
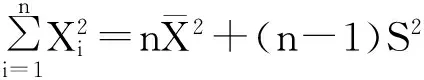
由于Y1,Y2相互独立,则(Y1,Y2)的联合密度为：

对-∞

令

由于T～t(n-1),U～χ2(n),即T与U的密度函数分别为：

-∞

由此得(T,U)的联合密度为：

得到T与U相互独立.

[1]BIRNBAUM Z W, SAUNDERS S C. A new family of life distribution[J]. Journal of Applied Probability,1969(6):319-322.

[2]DESMOND A F. Stochastic models of failure in random environments[J]. The Canadian Journal of Statistics,1985(2):171-176.

[3]DESMOND A F. On the relationship between two fatigue-life models[J]. IEEE Transactions on Reliability,1986(2):167-171.

[4]BIRNBAUM Z W, SAUNDERS S C. Estimation for a family of life distributions with applications to fatigue[J]. Appl Prob, 1969(6):328-347.

[5]ENGELHARDT M, WRIGHT F T. Inferences on the parameters of the Birnbaum Saunders fatigue life distribution based on maximum likelihood estimation[J]. Technometrics,1981,23(3):251-256.

[6]RIECK J R, NEDELMAN J R. A log-linear model for the Birnbaum Saunders distribution[J]. Techanometrics,1991,33(1):51-60.

[7]NG H K T, KUNDU D, BALAKRISHNAN N. Modified moment estimation for the two-parameter Birnbaum-Saunders distribution[J]. Computational Statistics and Data Analysis,2003,43:283-298.

[8]DUPUIS D J, MILLS J E. Robust estimation of the Birnbaum distribution[J]. IEEE Transactions on Reliability,1998,47(1):88-95.

[9]CHANG D S, TANG L C. Reliability bounds and critical time for the Birnbaum-Saunders distribution[J]. Reliability, IEEE Transactions on Reliability,1993,42:464-469.

[10]RIECK J R. Parametric estimation for the Birnbaum-Saunders distribution based on symmetrically censored samples[J]. Communication Statistics-Theory Methods,1995,24:1721-1736.

[11]OWEN W J, PADGETT W J. A Birnbaum-Saunders accelerated life model[J]. IEEE Transactions on Reliability,2000,49(2):224-229.

[12]OWEN W J, PADGETT W J. Acceleration models for system strength based on Birnbaum-Saunders distribution[J]. Lifetime Data Analysis,1999(5):133-147.

[13]OWEN W J, PADGETT W J. Power-law accelerated Birnbaum-Saunders life models[J]. International Journal of Reliability, Quality and Safety Engineering,2000,7(1):1-15.

[14]KUNDU D, KANNAN N, BALAKRISHNAN N. On the hazard function of Birnbaum-Saunders distribution and associated inference[J]. Computational Statistics & Data Analysis,2008,52(5):2692-2702.

[15]王炳兴,王玲玲.Birnbaum-Saunders疲劳寿命分布的参数估计[J].华东师范大学学报,1996(4):10-15.

WANG Bingxing, WAGN Lingling. Parameter estimation of Birnbaum-Saunders fatigue life distribution[J]. Journal of East China Normal University,1996(4):10-15.

[16]王炳兴,王玲玲.Birnbaum-Saunders疲劳寿命分布在截尾试验情形的统计分析[J].应用概率统计,1996,12(4):369-375.

WANG Bingxing, WAGN Lingling. Statistical analysis of Birnbaum-Saunders fatigue life distribution in the censored test case[J]. Applied Probability and Statistics,1996,12(4):369-375.

[17]王蓉华,费鹤良.双边截尾场合下BS疲劳寿命分布的参数估计[J].上海师范大学学报,1999,28(2):17-22.

WANG Ronghua, FEI Heliang. Parameter estimation for the BS fatigue life distribution under bilateral censoring[J]. Journal of Shanghai Normal University,1999,28(2):17-22.

[18]WANG Ronghua, FEI Heliang. Statistical analysis for the Birnbaum-Saunders fatigue life distribution under multiply type II censoring[J]. Chin Quart J of Math,2006,21(1):15-27.

[19]WANG Ronghua, FEI Heliang. Statistical analysis for the Birnbaum-Saunders fatigue life distribution under type II bilateral censoring and multiply type II censoring[J]. Chin Quart J of Math,2004,19(2):126-132.

[20]孙祝岭.Birnbaum-Saunders疲劳寿命分布尺度参数的区间估计[J].兵工学报,2009,30(11):1558-1561.

SUN Zhuling. Interval estimation of scale parameter for Birnbaum-Saunders fatigue life distribution[J]. Acta Armamentarii,2009，30(11)：1158-1561.

[21]孙祝岭.Birnbaum-Saunders疲劳寿命分布参数的回归估计方法[J].兵工学报,2010,31(9):1260-1262.

SUN Zhuling. Regression estimation method of parameters for Birnbaum-Saunders fatigue life distribution[J]. Acta Armamentarii,2010,31(9):1260-1262.

[22]孙祝岭.疲劳寿命分布变异系数的统计推断[J].质量与可靠性,2013(1):13-15.

SUN Zhuling. Statistical inference of variable coefficient for fatigue life distribution[J]. Quality and Reliability,2013(1):13-15.

[23]孙祝岭. Birnbaum-Saunders分布环境因子的置信限[J]. 强度与环境,2012,39(4):51-55.SUN Zhuling. Confidence limit of environmental factor for Birnbaum-Saunders distribution[J]. Structure & Environment Engineering,2012,39(4):51-55.

[24]WANG B X. Generalized interval estimation for the Birnbaum-Saunders distribution[J]. Computational Statistics and Data Analysis,2012,56:4320-4326.

[25]NIU Cuizhen, GUO Xu, XU Wangli, et al. Comparison of several Birnbaum-Saunders distributions[J]. Journal of Statistical Computation and Simulation,2014,84(12):2721-2733.

[26]周磊,孙玲玲.一种基于概率解释的新型互连线时延Slew模型[J].电路与系统学报,2009,14(2):7-10.

ZHOU Lei, SUN Lingling. A new Slew interconnect delay model Based on probability interpretation[J]. Journal of Circuits and Systems,2009,14(2):7-10.

[27]赵建印,孙权,彭宝华,等.基于加速退化数据的BS分布的统计推断[J].电子产品可靠性与环境试验,2006(1):11-14.

ZHAO Jianyin, SUN Quan, PENG Baohua, et al. Statistical inference for BS distribution based on the accelerated degradation data [J]. Electronic Product Reliability and Environmental Test,2006(1):11-14.

[28]徐晓岭,王蓉华.概率论与数理统计[M].北京：人民邮电出版社,2014:48-52.

XU Xiaoling, WANG Ronghua. Probability and Mathematical Statistics[M]. Beijing：Posts and Telecom Press,2014:48-52.

Two notes of statistical analysis about two-parameter Birnbaum-Saunders fatigue life distribution.

XU Xiaoling1, WANG Ronghua2, GU Beiqing1

(1.SchoolofStatisticsandInformation,ShanghaiUniversityofInternationalBusinessandEconomics,Shanghai201620,China; 2.MathematicsandScienceCollege,ShanghaiNormalUniversity,Shanghai200234,China)

We know that two methods about interval estimate of scale parameter for two-parameter Birnbaum-Saunders fatigue life distribution are shown not always capable of obtaining the interval estimate of scale parameter based on the results of Monte Carlo simulations. Moreover, there is a mistake in deriving the confidence intervals of scale parameter and parameter function with the generalized pivot method. A corresponding counter example is illustrated, and the correct proof is provided.

two-parameter Birnbaum-Saunders fatigue life distribution; scale parameter; interval estimate; generalized pivotal quantity

2015-12-04.

国家自然科学基金资助项目(11671264).

徐晓岭(1965-)，ORCID:http：//orcid.org/0000-0002-9442-8555,男，博士，教授，主要从事应用统计研究，E-mail:xlxu@suibe.edu.cn.

ORCID:http//orcid.org/0000-0003-1539-8747,E-mail:gubeiqing@suibe.edu.cn.

10.3785/j.issn.1008-9497.2016.05.008

O 213

A

1008-9497(2016)05-539-06