一维双极量子能量输运稳态模型弱解的存在性

董建伟， 程春蕊， 王艳萍

(郑州航空工业管理学院 理学院， 河南 郑州 450015)



一维双极量子能量输运稳态模型弱解的存在性

董建伟， 程春蕊， 王艳萍

(郑州航空工业管理学院 理学院， 河南 郑州 450015)

在一维有界区域上研究一个半导体双极量子能量输运稳态模型.将此模型变形为由2个四阶椭圆方程和1个二阶退化椭圆方程组成的耦合方程组.利用截断方法和Leray-Schauder不动点定理证明了其变形后方程组弱解的存在性.

量子能量输运模型；稳态解；存在性

Journal of Zhejiang University(Science Edition), 2016,43(5):521-524

量子漂移扩散模型、量子能量输运模型和量子流体动力学模型为半导体器件中常见的三大宏观量子模型.通过宏观量，例如电子密度、空穴密度、电流密度、粒子温度和电位势描述半导体器件中的载流子运动规律.最近，JUNGEL等[1]从完整的量子流体动力学模型中推导出简化的量子能量输运模型：

(1)

-div(n▽T)=n(TL(x)-T)，

(2)

ΔV=n-C(x)，

(3)

其中，电子密度n、电子温度T和电位势V为未知函数，晶格温度TL(x)和杂质密度C(x)为已知函数，普朗克常数ε>0为物理参数.在周期边界条件下，文献[1]首先证明了式(1)～(3)弱解的整体存在性，后来文献[2]研究了其解的半古典极限状态(ε→0).最近，文献[3]证明了式(1)～(3)的一维稳态模型古典解的存在性.关于式(1)～(3)不带量子项(即ε=0)的经典能量输运模型方面的研究结果见文献[4-5].当T=TL(x)=常数时，式(1)～(3)即变为量子漂移-扩散模型，近几年对此类模型已有大量研究成果[6-15].

1　主要结果

在一维有界区域(0,1)上研究式(1)～(3)的双极稳态模型：

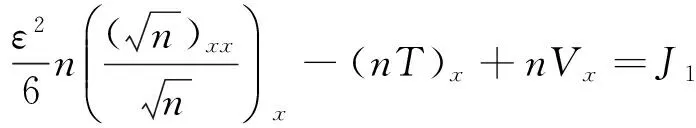
(4)

(5)

-((n+p)Tx)x=(n+p)(TL(x)-T),

(6)

Vxx=n-p-C(x)，x∈(0,1)，

(7)

n(0)=n(1)=1,p(0)=p(1)=1，

(8)

nx(0)=nx(1)=px(0)=px(1)=

Tx(0)=Tx(1)=0,

(9)

其中电子密度n、空穴密度p、粒子温度T和电位势V为未知函数，晶格温度TL(x)和杂质密度C(x)为已知函数，常数J1,J2分别表示电子电流密度和空穴电流密度.

式(4)、(5)分别除以n,p，再关于x求导，并利用式(7)得

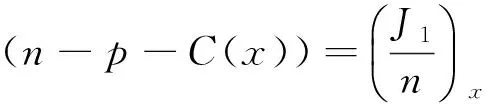
(10)

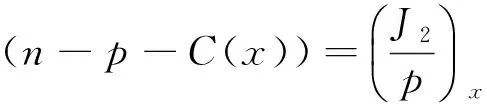
(11)

令n=eu，p=ev，则式(10),(11),(6),(8),(9)相应变为

(eu-ev-C(x))=J1(e-u)x，

(12)

(eu-ev-C(x))=J2(e-v)x，

(13)

-((eu+ev)Tx)x=(eu+ev)(TL(x)-T),

(14)

u(0)=u(1)=0,v(0)=v(1)=0,

(15)

ux(0)=ux(1)=vx(0)=vx(1)=

Tx(0)=Tx(1)=0.

(16)

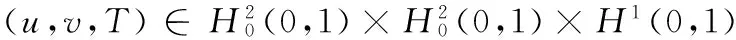
(17)

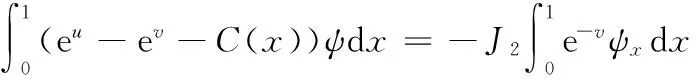
(18)

(19)

本文的主要结果为：

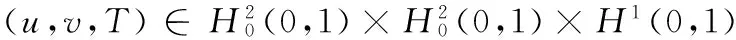
2　定理1的证明

先考虑式(17)、(18)和如下截断问题：

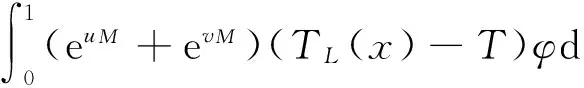
(20)

其中,uM=min{M,max{-M,u}}，常数M的定义见后文的式(25)，vM的定义与uM类似.

(21)

另外，有

(22)

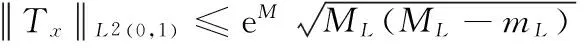
(23)

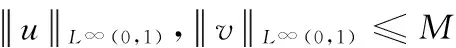
(24)

其中，

(25)

证明用φ=(T-ML)+=max{0,T-ML}∈H1(0,1)作为式(20)的试验函数，得

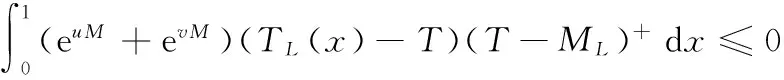
用φ=T∈H1(0,1)作为式(20)的试验函数，得

2eM(ML-mL)ML，

所以式(23)成立.

(26)

由Young不等式及式(23)，可以估计式(26)的右端第1项：

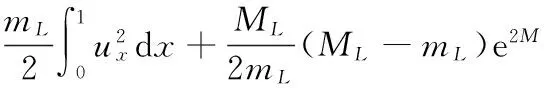
又因为

所以由式(26)可得

(27)

(28)

式(27)与(28)两边分别相加，得

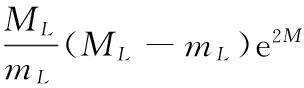
(29)

由Young及Poincare不等式知，

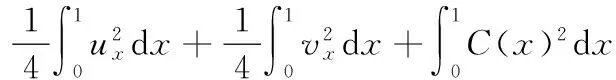
又因为

所以由式(29)可推得式(21).

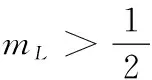
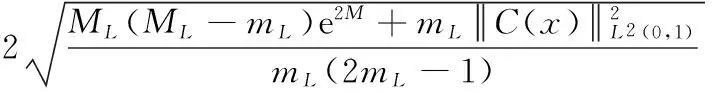
(30)

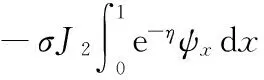
(31)

其中，σ∈[0,1]，定义双线性形式

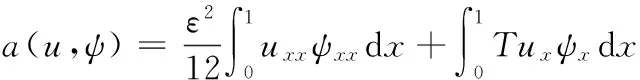
(32)

线性泛函

[1]JUNGEL A, MILISIC J P. A simplified quantum energy-transport model for semiconductors[J]. Nonlinear Analysis: Real World Applications, 2011,12(2):1033-1046.

[2]CHEN L, CHEN X Q, JUNGEL A. Semiclassical limit in a simplified quantum energy-transport model for semiconductors [J]. Kinetic and Related Models,2011,4(4):1049-1062.

[3]DONG J W, ZHANG Y L, CHENG S H. Existence of classical solutions to a stationary simplified quantum energy-transport model in 1-dimensional space[J]. Chinese Annals of Mathematics： Ser B, 2013,34(5):691-696.

[4]JUNGEL A, PINNAU R, ROHRIG E. Existence analysis for a simplified energy-transport model for semiconductors [J]. Math Meth Appl Sci,2013,36(13):1701-1712.

[5]董建伟，琚强昌.一个一维半导体简化能量输运模型的稳态解[J].数学年刊：A辑,2014,35(5):613-622.

DONG Jianwei, JU Qiangchang. A stationary solution to a 1-dimensional simplified energy-transport model

for semiconductors[J]. Chinese Annals of Mathematics： SerA,2014,35(5):613-622.

[6]JUNGEL A, VIOLET I. The quasi neutral limit in the quantum drift-diffusion equations [J]. Asymptotic Analysis,2007,53(3):139-157.

[7]CHEN L, JU Q C. Existence of weak solution and semiclassical limit for quantum drift-diffusion model[J]. Z Angew Math Phys,2007,58(1):1-15.

[8]CHEN X Q. The global existence and semiclassical limit of weak solutions to multidi-mensional quantum drift-diffusion model[J]. Advanced Nonlinear Studies,2007,7(1):651-670.

[9]CHEN X Q, CHEN L, JIAN H Y. The dirichlet problem of the quantum drift-diffusion model[J]. Nonlinear Analysis,2008,69(9):3084-3092.

[10]CHEN X Q, CHEN L. Initial time layer problem for quantum drift-diffusion model[J]. J Math Anal Appl,2008,343(1):64-80.

[11]CHEN X Q, CHEN L, JIAN H Y. Existence, semiclassical limit and long-time behavior of weak solution to quantum drift-diffusion model[J]. Nonlinear Analysis: Real World Applications, 2009,10(3):1321-1342.

[12]CHEN X Q. The isentropic quantum drift-diffusion model in two or three space dimensions[J]. Z Angew Math Phys,2009,60(3):416-437.

[13]NISHIBATA S, SHIGETA N, SUZUKI M. Asymptotic behaviors and classical limits of solutions to a quantum drift-diffusion model for semiconductors [J]. Mathematical Models and Methods in Applied Sciences,2010,20(6):909-936.

[14]DONG J W. Classical solutions to the one-dimensional stationary quantum drift-diffusion model[J]. Journal of Mathematical Analysis and Applications,2013,399(2):594-598.

[15]董建伟，张伟.关于一维稳态量子漂移-扩散模型[J].数学进展，2015,44(2):263-270.

DONG Jianwei, ZHANG Wei. On the stationary quantum drift-diffusion model in one space dimension [J]. Advances in Mathematics,2015,44(2):263-270.

Existence of weak solutions to a stationary 1-dimensional bipolar quantum energy-transport model.

DONG Jianwei, CHENG Chunrui, WANG Yanping

(SchoolofMathematicsandPhysics,ZhengzhouInstituteofAeronauticalIndustryManagement,Zhengzhou450015,China)

A stationary bipolar quantum energy-transport model for semiconductors is studied in a 1-dimensional bounded domain. The model is reformulated as a coupled system consisting of two fourth-order elliptic equations and a second-order degenerate elliptic equation. The existence of weak solutions to the reformulated system is proved using the truncation method and the Leray-Schauder fixed-point theorem.

quantum energy-transport model; stationary solutions; existence

2015-10-15.

河南省科技厅基础与前沿技术研究计划项目 (162300410077)；航空科学基金项目(2013ZD55006)；河南省高等学校青年骨干教师资助计划项目(2013GGJS-142)；郑州航空工业管理学院青年科研基金项目(2013111001，2014113002，2015113001).

董建伟(1980-)，ORCID:http//orcid.org/0000-0003-1131-8244，男，硕士，副教授，主要从事偏微分方程研究，E-mail:dongjianweiccm@163.com.

10.3785/j.issn.1008-9497.2016.05.004

O 175.2

A

1008-9497(2016)05-521-04