煤液化弯管冲蚀磨损的数值模拟研究

邵 东,王建文

(华东理工大学 机械与动力工程学院，上海 200237)



应用技术

煤液化弯管冲蚀磨损的数值模拟研究

邵 东,王建文

(华东理工大学 机械与动力工程学院，上海 200237)

针对煤液化工业管道系统中弯管部位的冲蚀磨损问题，通过二次开发将磨损模型嵌入到FLUENT中模拟计算磨损率大小及磨损位置，将计算结果与试验数据相对比以验证模型的正确性，再将磨损模型应用到煤液化管道的冲蚀磨损预测研究中。结果表明：煤粉直径小于80 μm时，磨损率随着粒径增大明显降低；最大磨损率与冲击速度成指数增长；最大磨损率随着管道弯曲角度增大而降低；弯径比为3时磨损率较小且磨损分布均匀。

油煤浆；弯管；固-液两相流；冲蚀磨损；数值模拟

煤直接液化技术是将干燥的煤磨成小于200目的细粉，并配制成油煤浆；预热至350 ℃，加压到15～30 MPa，使煤软化、热解、变为胶状物；再在反应器内高温、高压、催化剂条件下加氢反应[1]。采用煤液化技术，将煤转化成油品和化工产品，是缓解石油压力、提高煤炭资源利用率、降低环境污染的重要途径[2]。煤液化过程中，因多相流冲蚀磨损引发的失效、非计划事故频繁发生，尤其对冲击和腐蚀交互作用下的冲蚀破坏更为严重。研究表明，管道系统中弯管部位的冲蚀磨损比直管部位高50倍[3]。在停工检修时，由于缺乏检测区域的针对性和检测时间的合理性，即增加了运行成本，又难以保障企业的安全生产。

本工作采用数值计算方法研究了油煤浆对输送管道弯管部位的冲蚀磨损规律，通过二次开发，将磨损模型嵌入到FLUENT软件中，数值计算冲蚀磨损率大小和磨损位置分布。分析对比不同管道结构、粒子属性等因素对冲蚀磨损的影响，为管道设计、工艺设计以及管道系统壁厚监测提供了依据。

1　计算模型

1.1几何模型与边界条件

选取公称直径(DN)为200 mm，弯径比为3，弯曲角度为90°的管道为例来进行分析。如图1所示：L1为管道入口直管段长度，L2为出口直管段长度，d为管道内径，R为弯管曲率半径，为了保证油煤浆流经弯管时是充分发展的湍流流动，取L1=12d，L2=10d[4]。

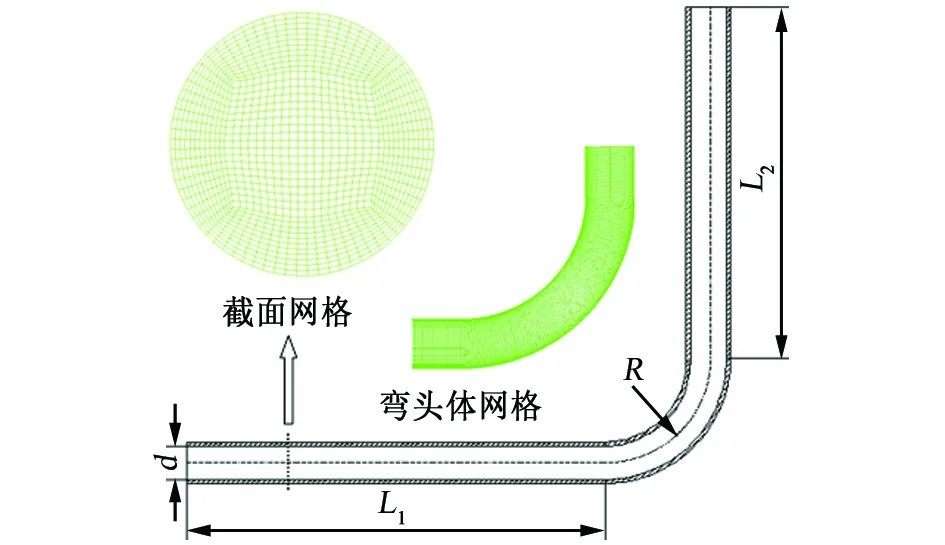
图1　管道几何模型及网格Fig. 1　Geometry model and mesh of pipeline

利用UG建立物理模型，ICEM划分网格，采用截面扫略法划分六面体网格，截面采用“古钱币”式平面圆分网算法[5]，见图1。

管道材料采用Inconel 718，密度为8 240 kg/m3，布氏硬度为363 N/mm2。管内液相密度为797.5 kg/m3，黏度为0.008 Pa·s；煤粉密度为1 728 kg/m3，粒径分布为5～200 μm，平均粒径为74 μm，颗粒规整度用形状系数表示，在0.2～1之间选取，颗粒体积分数为2.5%。

温度较高时，油煤浆可近似按牛顿流体计算[6]，且油煤浆为固-液混合物，可视为不可压流体，在假设常物性参数和能量守恒的条件下，管内流体满足连续性方程和动量方程。计算时湍流模型采用标准的κ-ε方程，压力-速度耦合采用SIMPLE算法，动量方程、压力、湍动能和湍流扩散率均采用Quick格式。入口和出口边界采用速度入口和压力出口，壁面采用无滑移边界和标准壁面函数，同时考虑流体和颗粒间的双向耦合作用。

1.2颗粒轨迹模型

FLUENT通过积分拉氏坐标系下颗粒的作用力微分方程来求解颗粒的轨道。固体颗粒在笛卡尔坐标系下沿x方向的微分方程[7]见式(1)：

(1)

式中：u为连续相的速度，m/s；up为颗粒相的速度，m/s；FD(u-up)为颗粒的单位质量曳力；ρp和ρ分别为颗粒和油浆的密度；Fx为其他附加力，N；在所有作用力中，只考虑Saffman升力和重力的作用，其他作用力非常小，可以忽略不计[8]。

1.3磨损模型

目前，比较常用的磨损模型包括Finne切削磨损模型[9]、Hashish和Bitter的剪切和变形磨损模型[10]、Tulsa大学的冲蚀磨损模型[11]和Oka磨损模型[12]。

分别将Tulsa大学的冲蚀磨损方程和Hashish改进的剪切磨损模型嵌入到FLUENT中进行煤液化管道冲蚀磨损预测研究，见式(2)～(4)：

(2)

(3)

(4)

式中：Wt为壁面材料的冲蚀磨损率，kg/(m2·s)；C为常数；HB为壁面材料的布氏硬度，N/mm2；mp为固体颗粒的质量流率，kg/s；Fs为颗粒的形状系数；Vp为颗粒的冲击速率，m/s；n为速率指数，取2.41；F(θ)为冲击角度函数；Ac为计算单元的面积，m2；ρw为壁面材料的密度，kg/m3；Mp为颗粒质量，kg；rp为颗粒半径，m；Ck为剪切特征速率，m/s；σ为管道塑性流动应力，Pa；ρp为颗粒密度kg/m3。

Tulsa大学的冲蚀磨损模型中的冲击角度函数分别采用式(5)和式[11](6)计算，以下分别简称为Tulsa(1)模型和Tulsa(2)模型。

(5)

(6)

式中：θ为颗粒与壁面的冲击角度，rad；k1～k5为根据壁面材料确定的经验常数。

2　磨损模型验证

为了验证磨损模型的正确性，将数值计算得出的结果与Bourgoyne的试验数据[13]进行对比。试验采用的管道直径为52.5 mm，材料为ASTM A216 Grade WCB，硬度为140 HB，密度为7 800 kg/m3；流体介质为泥浆，黏度为0.06 Pa·s；固体颗粒为半圆形的石英砂，颗粒直径为350 μm。由数值计算和试验得到的最大磨损率结果见表1。通过对比分析，数值计算得到的结果与试验结果表现出良好的一致性，因而可以用来预测煤液化管道的冲蚀磨损情况。

3　计算结果

3.1网格无关性验证

使用Tulsa(1)模型进行验证。由图2可知，当网格数量达到51万时计算结果基本稳定，在计算误差允许的前提下，为了尽可能减小计算误差，本次计算选取的网格数为513 780。

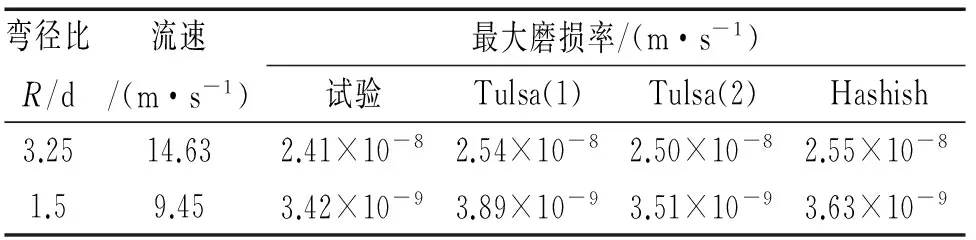
表1　冲蚀磨损数值计算与试验数据对比Tab. 1　The numerical calculation of erosion wear compared with experimental data

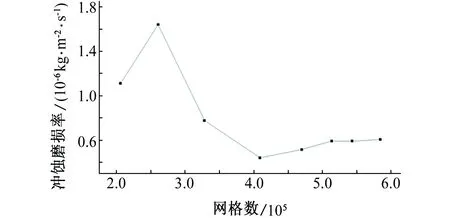
图2　最大冲蚀磨损率与网格数量的关系Fig. 2　The relationship of maximum erosion wear rate and grid number

3.2速度分布

以入口速度V=5 m/s，DN200 mm，R/d=3，弯曲角度为90°管道为例，速度分布如图3所示(图中截面的上部为管道的内拱壁)。

由图3可知，入口直管段速度分布比较均匀，当介质刚流进弯管时，由于内拱壁一侧流道变化较外拱壁一侧更剧烈，使得介质在内拱壁处的流速迅速增大，随后介质沿着管道壁面做圆周运动，在离心力作用下，使得介质在管道外拱壁近壁面的流速大于内拱壁近壁面的，外拱壁处的压强高于内拱壁的。介质除了沿管壁的圆周运动以外，还存在由管道外拱壁向内拱壁沿横截面切线方向上的圆周运动，即“二次流”，在弯头45°处至弯头出口部位二次流更加明显。当介质流出弯管时，在出口直管段流速逐渐恢复均匀分布，二次流也逐渐消失，见图3。

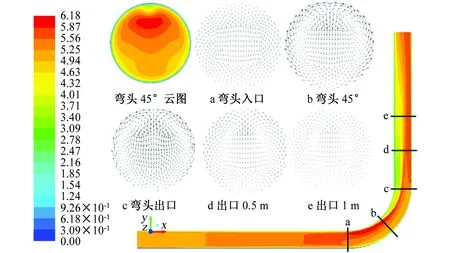
图3　管道及截面速度分布云图(m/s)Fig. 3　The velocity distribution cloud of pipeline and sectional velocity (m/s)

3.3冲蚀磨损

选取DN200 mm，R/d=3，弯曲角度为90°管道，入口速度V=5 m/s，直径为74 μm的半球形颗粒进行分析(在以下的影响因素分析计算中只改变其中某一参数，其他参数均保持不变)。三种磨损模型计算得到的最大冲蚀磨损率位置基本一致，只是Hashish模型得到的冲蚀面积较小。

煤液化管道冲蚀磨损主要是由油煤浆中的煤粉颗粒对管壁的冲击造成的，当油煤浆流入弯头部位时，由于流道几何形状发生改变，油煤浆会对管道产生很大的冲蚀磨损作用，该部位的磨损有两部分组成：(a) 沿着弯管壁面做圆周运动的主动流造成的冲击磨损，称为“主动流磨损”，主要发生在弯管的外拱壁处；(b) 油煤浆流经弯管时产生的二次流造成的磨损，称为“二次流磨损”，主要发生在弯管的侧壁。在靠近弯头出口部位的直管段，由于流速还没有完全恢复均匀分布，存在湍流脉动，故也会有一定冲击磨损，但数值很小。

3.4磨损影响因素分析

三种磨损模型在不同条件下模拟计算得到磨损率变化规律和磨损位置分布情况基本一致，如无特别说明，磨损云图均以Tulsa(1)模型的计算结果进行分析。

3.4.1 颗粒直径的影响

保持其他条件不变的情况下，分别采用Tulsa(1)模型、Tulsa(2)模型和Hashish模型计算不同粒子直径对冲蚀磨损的影响。得到的最大冲蚀磨损率见图4。

当粒径小于80 μm时，随着粒子直径增大，最大磨损率明显降低。这是因为煤粉颗粒体积不变时，随着粒子直径增大，颗粒数目减小，流体对颗粒的携带作用下降。当粒子直径大于80 μm时，最大磨损率随颗粒直径的变化平缓。

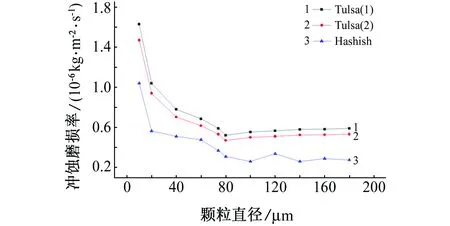
图4　最大冲蚀磨损率与颗粒直径的关系Fig. 4　The relationship of maximum erosion wear rate and particle diameter

由图5可见，颗粒直径较小时，最大磨损位置在弯头的内拱壁处；随着颗粒直径增大，最大冲蚀磨损率的位置逐渐从弯头部位的内拱壁向外拱壁、侧壁方向移动，且冲蚀磨损的面积也逐渐增大。这主要因为随着粒径增大，颗粒动量增大，流体携带作用下降。三个磨损方程计算结果基本一致。

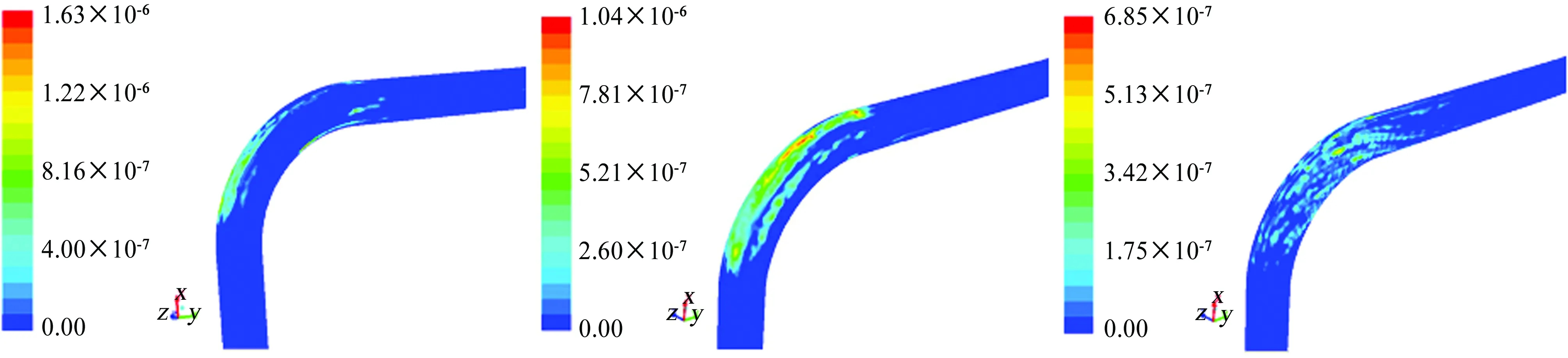
(a)　10 μm (b)　20 μm (f)　60 μm

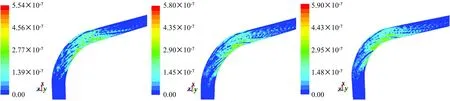
(d)　100 μm (e)　140 μm (i)　180 μm图5　不同颗粒直径对应的冲蚀磨损云图Fig. 5　The erosion wear cloud of different particle diameters

3.4.2 入口速度的影响

其他条件不变，随着入口速度增大，最大冲蚀磨损率成指数增长，Hashish磨损模型计算得到的增长指数小于Tulsa磨损模型的，见图6。

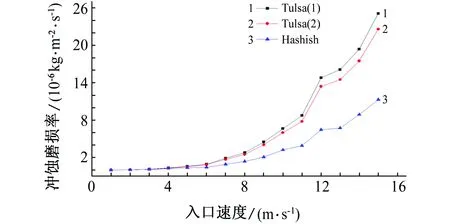
图6　最大冲蚀磨损率与入口速度的关系Fig. 6　The relationship of maximum erosion wear rate and inlet velocity

另外，随着入口速度增大，最大冲蚀磨损位置逐渐由弯管外拱壁向侧壁和出口方向移动，且冲蚀面积也不断增大，如图7所示。

3.4.3 管道弯曲角度的影响

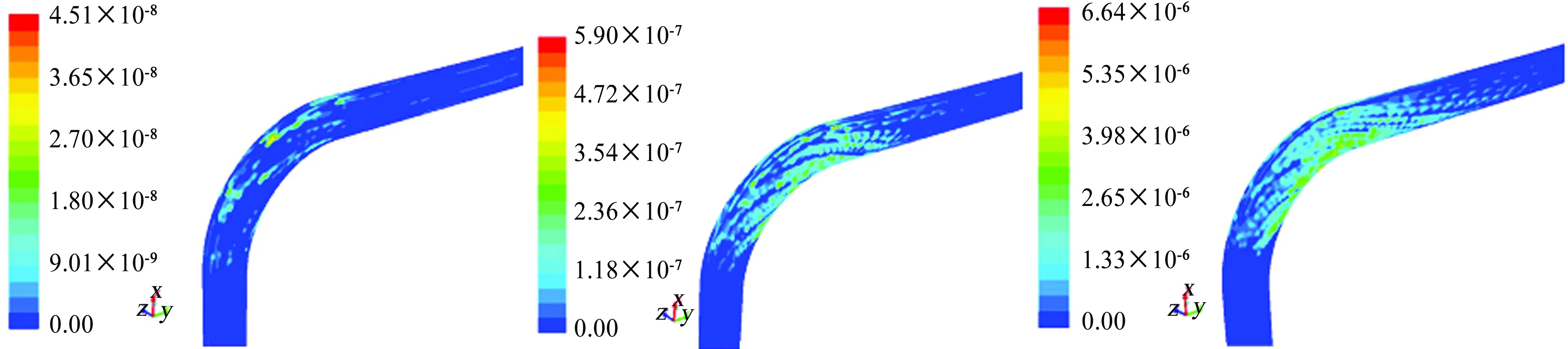
其他条件都不变，分别计算不同弯曲角度管道对应的冲蚀磨损云图，见图8。由图8可见,当弯曲角度小于90°时，最大冲蚀磨损率明显下降；当弯曲角度大于90°时，最大磨损率下降速度变缓。这是因为弯曲角度增大，流道几何形状发生改变，介质流经弯头的流动状态逐渐趋于平缓。随着弯曲角度的增大，最大磨损率的位置均发生在弯头出口处的外拱壁处；冲蚀磨损面积减小，但单位面积上的磨损量增大。

3.4.4 管道弯径比的影响

其他条件都不变，分别计算不同弯径比管道对应的冲击磨损情况，见图9。由图9可见,随着弯径比增大，最大冲磨损率位置由管道内侧壁向管道外侧壁和外拱壁处移动；冲蚀面积也增大。由图10可见，当弯径比小于3时，最大冲蚀磨损率随弯径比的增大明显降低；当弯径比大于3时，最大磨损率变化平缓。综合比较，弯径比为3时比较合适。

(a)　2 m/s (b)　5 m/s (c)　10 m/s图7　不同入口速度对应的冲蚀磨损云图Fig. 7　The erosion wear cloud of different inlet velocities

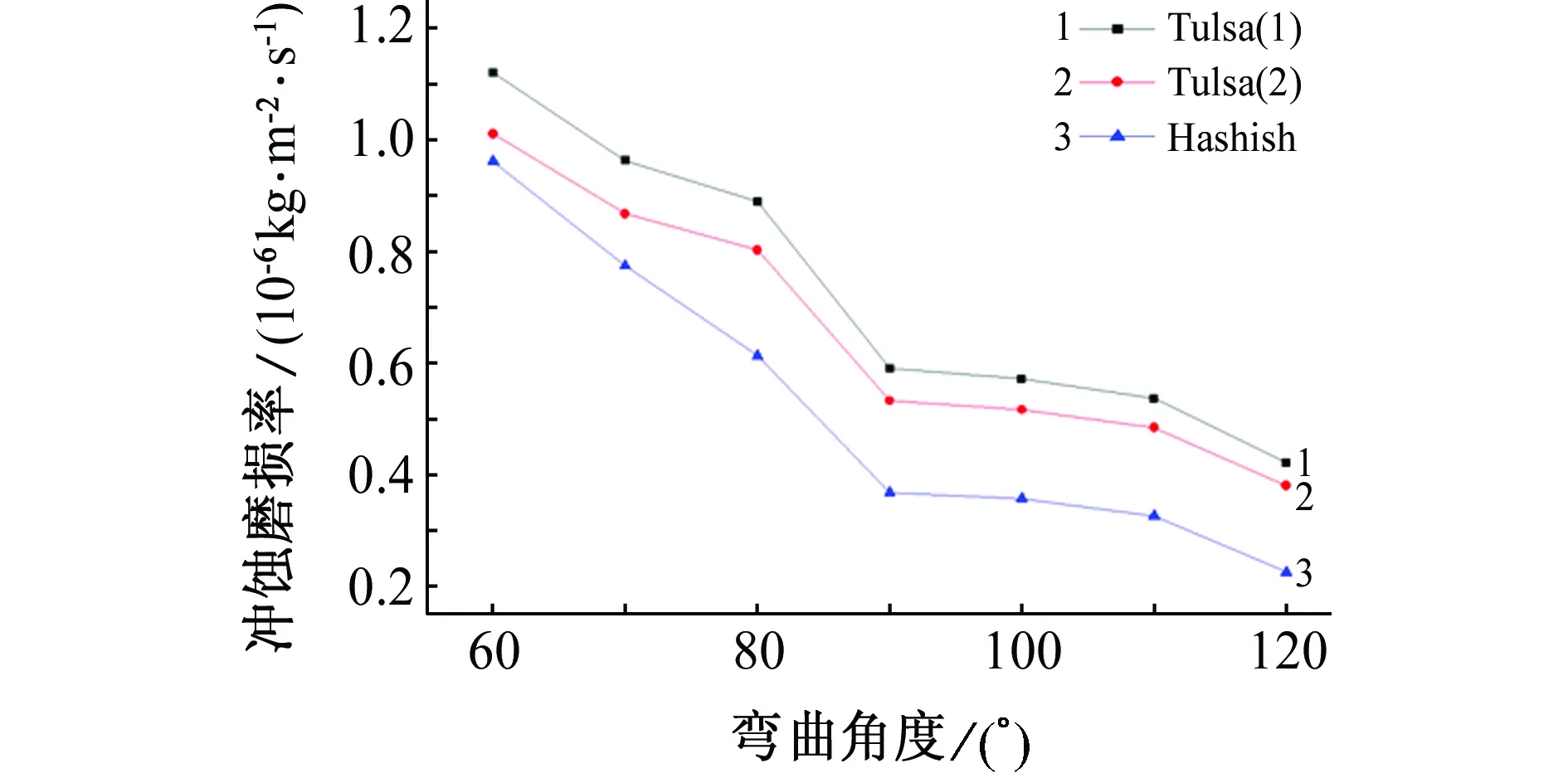
图8　最大冲蚀磨损率与弯曲角度的关系Fig. 8　The relationship of maximum erosion wear rate and bending angle

弯径比对冲蚀磨损产生影响，主要是由于弯头曲率半径不同时，介质流经弯管的流动状态不同。当弯径比较小时，弯头路径较短，流道方向变化大，使得油煤浆流动方向改变剧烈，速度变化较大，二次流也比较严重，如图11所示，从而造成比较严重的冲蚀磨损，磨损比较严重的区域为管道侧壁和外拱壁。当弯径比较大时，弯头路径较长，流道方向变化平缓，使得油煤浆流入弯头时流动方向改变比较平缓，流速变化小，且二次流随着弯径比的增大逐渐减小，从而造成较小的冲击磨损，磨损严重的区域为管道外拱壁。

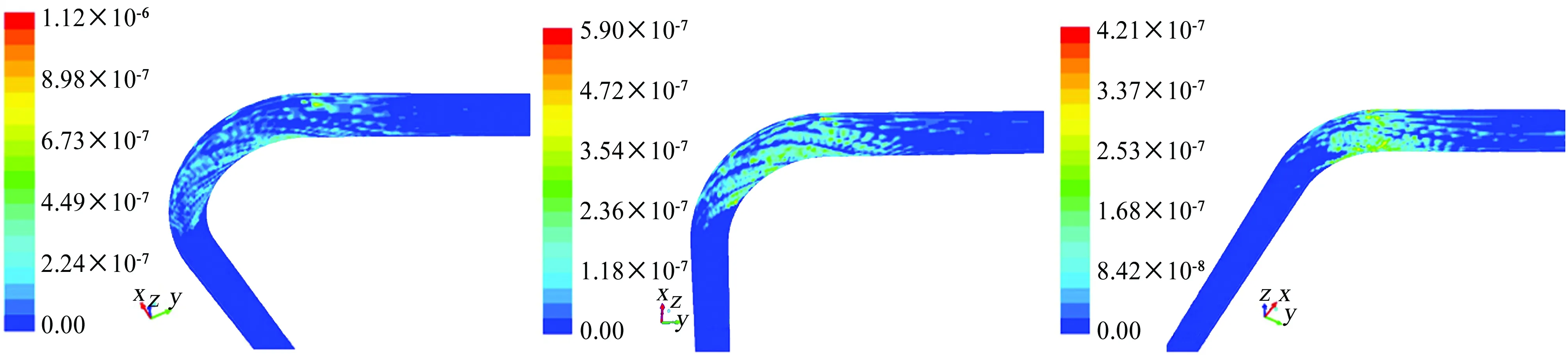
(a)　60° (b)　90° (c)　120°图9　不同弯曲角度对应的冲蚀磨损云图Fig. 9　The erosion wear cloud of different bending angles

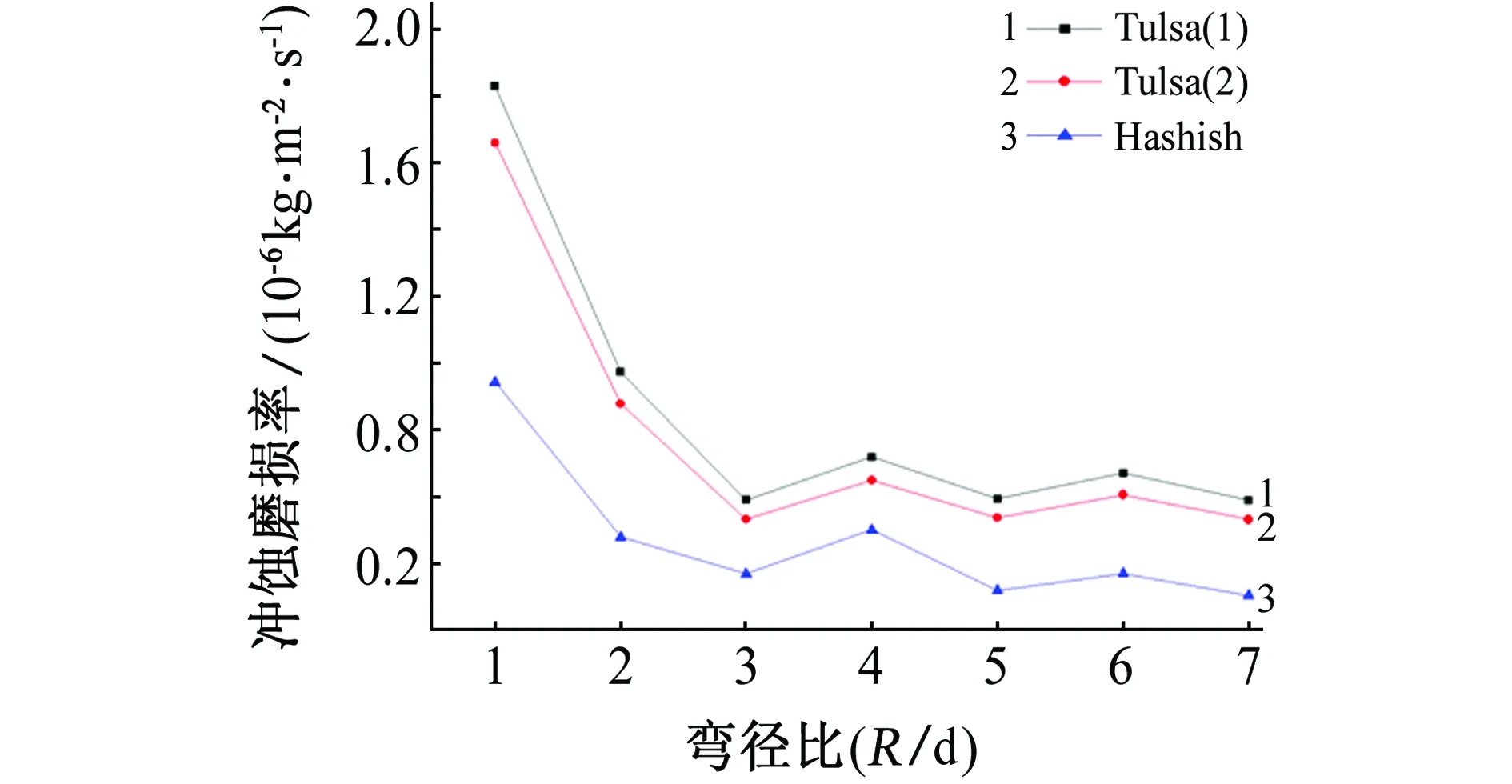
图10　最大冲蚀磨损率与弯径比的关系Fig. 10　The relationship of maximum erosion wear rate and bending diameter ratio

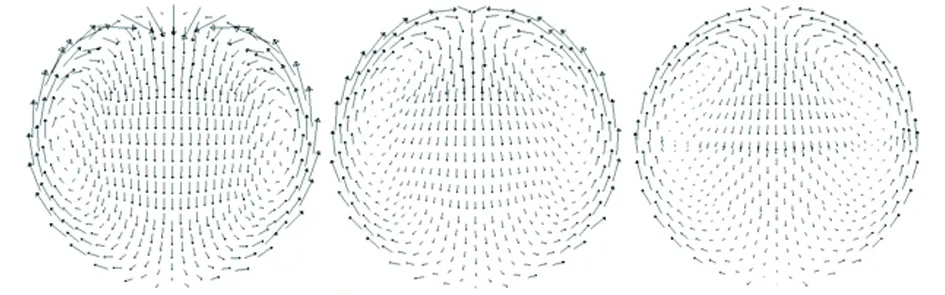
(a)　R/d=1 (b)　R/d=3 (c)　R/d=5图11　不同弯径比管道弯头45°截面二次流Fig. 11　The secondary flow of elbows 45 degree section for different bending diameter ratio pipes

4　结论

煤液化管道弯管部位在油煤浆冲击作用下磨损情况非常复杂，受诸多因素影响，保持其他条件不变：

(1) 当粒径小于80 μm时，随着粒径增大磨损率明显降低；当粒径大于80 μm时，磨损率变化比较平缓。

(2) 冲蚀磨损率与冲击速度呈指数增长关系。

(3) 管道弯曲角度越大，冲蚀磨损率越小，尤其是弯曲角度小于90°时，最大冲蚀磨损率明显降低，管道弯曲角度尽量选取90°或90°以上。

(4) 当R/d小于3时，随着弯径比增大，磨损率明显下降；当R/d大于3时，磨损率变化比较平缓；冲蚀磨损面积随着弯径比增大而增大，综合比较，取弯径比为3时较合适。

[1]李大尚. 煤制油工艺技术分析与评价[J]. 煤化工，2003,31(1):17-23.

[2]边钢月. 煤转化对炼油化工行业竞争力浅析[J]. 化学工业，2008,26(10):9-11.

[3]郑友取，张新育. 90°方形弯管内颗粒冲蚀磨损研究[J]. 热力发电，2007,36(4):34-36.

[4]黄卫星，陈文梅. 工程流体力学[M]. 北京：化学工业出版社，2002.

[5]FILIPIAK M. Mesh Generation[M]. Edinburgh Parallel Computing Centre：University of Edinburgh,1996.

[6]NOGAMI Y,YAMAURA J,INOKUCHI K,et al. Viscoelasticity of coal slurries[C]//Proceedings of the 4th Japan China Symposium on Coal and C1 Chemistry.Osaka:[s.n,],1993:395-398.

[7]程嘉瑞，杨向同. API油管接箍液固两相流体冲蚀数值模拟[J]. 腐蚀与防护，2013,34(12):1067-1069.

[8]BADR H M,HABIB M A,BEN-MANSOUR R,et al. Numerical investigation of erosion threshold velocity in a pipe with sudden contraction[J]. Computers and Fluids,2005,34(6):721-742.

[9]FINNE I,MCFADDEN D. On the velocity dependence of the erosion of ductile metals by solid particles at low angles of incidence[J]. Wear,1978,48(1):181-190.

[10]HASHISH M. An improved model of erosion by solid particles[C]//Proceeding of the 7th International Conference on Erosion by liquid and Solid Impact.Cambridge:Cavnedish Laboratory,1988:66.

[11]ZHANG Y,REUTERFORS E P,MCLAURY B S,et al. Comparison of computed and measured particle velocities and erosion in water and air flows[J]. Wear,2007,263(1/6):330-338.

[12]OKA Y I,OKAMURA K,YOSHIDA T. Particle estimation of erosion damage caused by solid particle impact.Part1,Part2:effects of impact parameters on a predictive equationp[J]. Wear,2005,259(1/6):95-101.

[13]WANG J R,SIAMACK A. A CFD based correlation for erosion factor for long-radius elbows an-d bends[J]. Journal of Energy Resources Technology,2003,125(1):26-34.

Numerical Simulation Research of Erosion Wear for Elbows in Coal Liquefaction

SHAO Dong, WANG Jian-wen

(College of Mechanical and Power Engineering, East China University of Science and Technology, Shanghai 200237, China)

The erosion model was inserted into FLUENT by secondary development to calculate the wear rate and simulate the wear position for the elbow erosion wear problem in coal liquefaction industry. The calculated results and test data were compared to validate the correctness of the model. Then the erosion model was applied to predict the erosion at the elbow region in coal liquefaction industry. The numerical results reveal that when the particle diameter was less than 80 μm, the maximum wear rate significantly decreased with the increase of particle diameter. Maximum wear rate grows exponential with the increase of impact velocity. The maximum wear rate decreased with the increase of pipe bending angle. Bend diameter ratio of 3 was more appropriate.

coal-oil slurry; elbow; solid-liquid flow; erosion wear; numerical simulation

10.11973/fsyfh-201605016

2015-03-17

王建文(1969-),副教授,博士,从事冲蚀-腐蚀失效研究,13916897136,wangjianwen@ecust.edu.cn

TG174

A

1005-748X(2016)05-0424-06