基于单调性视角下的函数综合题破解策略

江苏省丹阳市第五中学　(212300)

孔帮新



基于单调性视角下的函数综合题破解策略

江苏省丹阳市第五中学(212300)

孔帮新

函数是高中数学的主干内容，是研究变量数学的工具，是学习高等数学的基础，是历年高考考查的重点.而函数单调性则是函数性质的核心和灵魂，是函数试题的“心脏”.几乎所有的函数综合试题都与函数单调性紧密联系.函数单调性还与不等式、参数的范围、数列、三角函数、解析几何密切相关.下面笔者谈谈从函数单调性的视角破解函数综合题的策略，不到之处请批评指正.

一、以数驭形，构造函数，研究几何性质

例1(2014年苏北四市调研测试20题)

设函数f(x)=ax2+(1-2a)x-lnx(a∈R)的图像为曲线C，点A(x1,y1),B(x2,y2)是曲线上不同的两点，点M为线段AB的中点，过点M作x轴的垂线交曲线C于点N，试问曲线C在点N处的切线是否平行于直线AB，并说明理由.

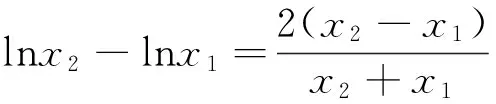
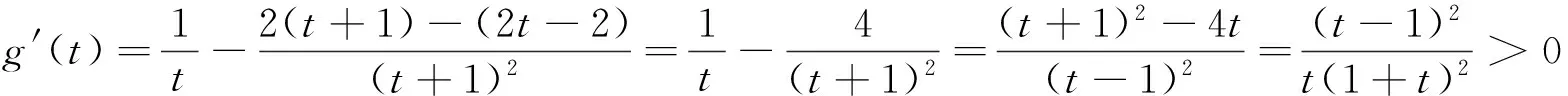
解决本问题的关键是将线线平行判断转化为构造新函数，运用函数单调性判断函数是否有零点.转化策略和求导数是工具.许多函数试题最终都转化为用函数单调性解决问题.

构造函数的基本原则是求导数、找零点、判断导函数值的符号方便，且具有比较明显的几何特征.

二、分析特征，合理放缩，证明不等式

例2(2013年高考全国新课标卷第21题)

已知函数f(x)=ex-ln(x+m).

(1)设x=0是f(x)的极值点，求m，并讨论f(x)的单调性；

(2)当m≤2时，证明f(x)>0.

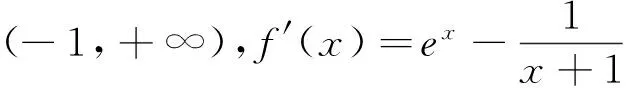
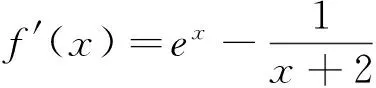
本题将证明不等式转化为判断函数的单调性，再次显示了函数单调性的威力.

三、合理转化，分类讨论，巧求参数范围

例3(2014年高考山东卷第20题)

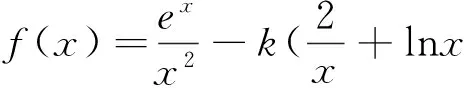
(1)当k≤0时，求函数f(x)的单调区间；

(2)若函数f(x)在(0,2)内存在两个极值点，求k的取值范围.

分析：求函数单调区间可通过求导数判断导数值在各区间的正负得到，如含参数则须分类讨论以便确定符号.f(x)在(0,2)内存在两个极值点，即f′(x)在(0,2)有两个零点，可转化研究f′(x)在(0,2)上的单调性和极值点的位置，根据f′(x)的单调性确定f′(x)在(0,2)的零点.

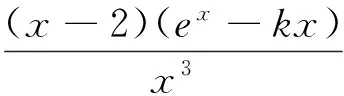
(2)由(1)知，当k≤0时,函数f(x)在(0,2)内单调递减，故f(x)在(0,2)内不存在极值点；当k>0时,设g(x)=ex-kx,x∈[0,+∞)，因为g′(x)=ex-k=ex-elnk，当00，y=g(x)单调递增，故f(x)在(0,2)内不存在两个极值点；

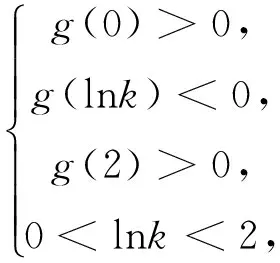
四、巧设函数，简化运算，破解恒成立问题

例4(2013年高考天津第20题)

已知函数f(x)=x-ln(x+a)的最小值为0，其中a>0.

(1)求a的值；

(2)若对任意的x∈[0,+∞)有f(x)≤kx2成立，求实数k的最小值.

(2)当k≤0时,取x=1有f(1)=1-ln2>0，故k≤0不合题意.当k>0时,令g(x)=f(x)-kx2，即g(x)=x-ln(x+1)-kx2，

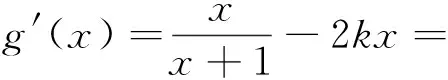
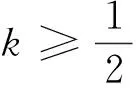
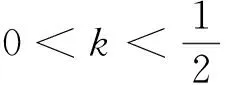
解后反思：恒成立问题其实是求新的函数g(x)=f(x)-kx2的最大值为0时实数k的范围，也即运用导数借助单调性，求出函数最值.因为新函数含参数，求导数，找极值点并判断导数的符号是难点.本题如按常规思路分离变量构造函数，则求导函数零点及判断函数值的正负号就非常繁.

总之，纵观函数综合题解法，可总结为以下步骤：

首先，弄清问题的条件有哪些，结论求什么？如判断函数单调性，求极值(最值)，比较函数值的大小，求零点个数，证明不等式等等均与函数单调性紧密联系；

其次，把所求结论转化，通过构造新函数或从原函数出发，求导数判断函数单调性，通常函数中含有参数需要分类讨论以判断导函数在给定区间的符号；

最后，结合函数在给定区间上的大致图像形状，数形结合，寻找结论.