再谈一道填空题的另解及妙解*

江苏省南京市第二十九中学　(210036)

郭建华

江苏省南京市金陵中学　　　(210005)

于　健



再谈一道填空题的另解及妙解*

江苏省南京市第二十九中学(210036)

郭建华

江苏省南京市金陵中学(210005)

于健

题目在ΔABC中，点D在边BC上，且DC=2BD，AB∶AD∶AC=3∶k∶1，则实数k的取值范围为_________.

文[1]从通观全局，宏观把握解题思路的角度探求该题的三种解法，强调对概念和通性通法的教学，很值得学习和研究.对此，在文[1]研究的基础上笔者对该题又做了一些解法的探究和思考，供大家参考.

受文[1]解法2的启发，将ΔABC放在坐标系中研究，根据题设条件，挖掘了问题的“隐性”轨迹，则使解题思路豁然开朗，于是得到下面的解法.

1　另解

解析：如图1，以点A为原点，AB为轴建立平面

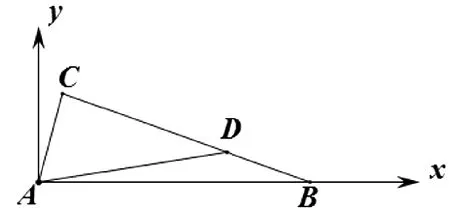
图1

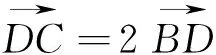
根据对题意的深刻理解和对图形的观察，通过添加辅助线的方法让解题变得由难到易，由繁到简，妙不可言，其解法如下.

2　妙解

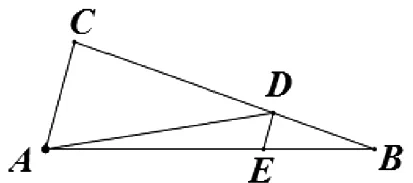
图2

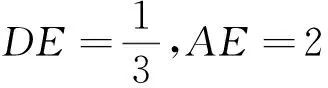
圆”，借助圆的定义及圆丰富的几何性质，沟通条件和结论的关系，大大简化计算过程，提高解题速度，事半功倍．在教师的引导下更多地为学生创造探究的元素，让学生体会转化思想在解题中的应用；“妙解”中通过数形结合，巧妙地添加辅助线，纯粹运用平面几何的相关知识求解，不仅提升解题的速度和准确度，而且使得解题过程更为简捷明了.因此在解题中要不断引导学生从不同角度分析问题，加强解题方法的对比，通过对题设条件的挖掘和再创造，寻求更好的求解方案.这样不仅有利于培养他们的钻研精神和创造能力，而且有利于思维灵活性的培养和陶冶他们的情操，体会数学给他们带来的快乐.

[1]刘增娣.宏观把握 追本溯源 让解题思路自然而生[J].中学数学研究(江西)，2015(2)：34-36.

[2]郭建华.“设而不求”5例[J].数理天地，2016(3)：12-13.

[3]郭建华.重视借题“发挥 ”拓展数学思维[J].中学教研2015(12)：6-8.

江苏省教育科学“十二五”规划立项课题 ：信息技术环境下高中数学“问题—探究—解决”教学模式的应用研究 (D/2013/02/445)的研究成果之一.