一题多解与一题多究
2016-08-25 05:30山东省聊城大学数学科学学院252000
中学数学研究(江西) 2016年6期
山东省聊城大学数学科学学院 (252000)
姜晓洁* 于兴江
一题多解与一题多究
山东省聊城大学数学科学学院(252000)
姜晓洁*于兴江
一题多解与一题多究可以深入了解题目的设计意图、设计方法,牢固掌握题目相关知识,是中学教师提升自身知识素质的最佳途径.笔者就2015年高考理科数学四川卷第20题为例,进行了多解分析和推广探究,并将本题推广到双曲线和抛物线上,得到了相似的结论.
1 原题呈现
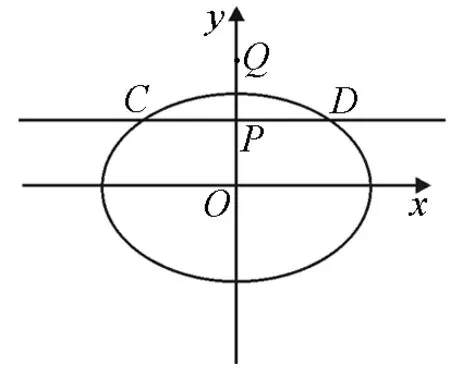
图1
(Ⅰ)求椭圆E的方程;
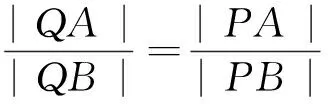
2 解法探究

|QD|.因此Q点在y轴上,设Q(0,y0).
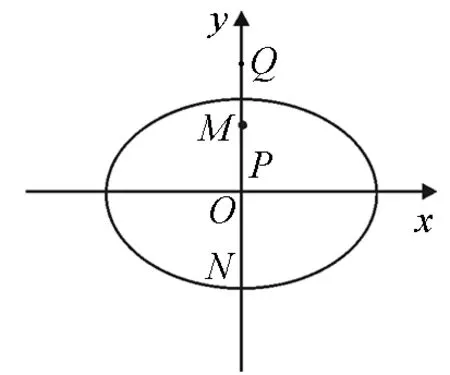
图2
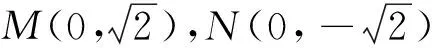
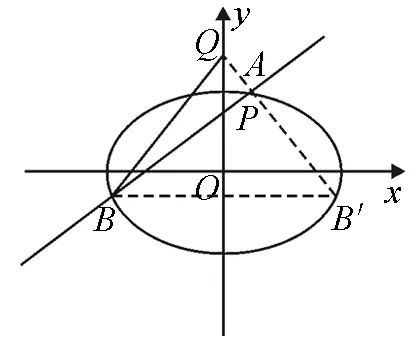
图3
以下证明,对任意的直线l,Q(0,2)均满足条件.
如图3,当直线l斜率不存在时,显然成立,以上已证.
当直线l斜率存在时,设直线l方程为y=kx+1,A(x1,y1),B(x2,y2).
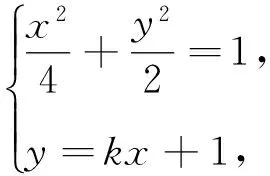
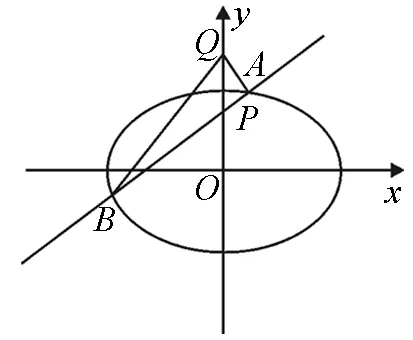
图4
解法2:由解法1可知,若存在不同于点P的定点Q,则只能是Q(0,2).以下证明,对任意的直线l,Q(0,2)均满足条件.
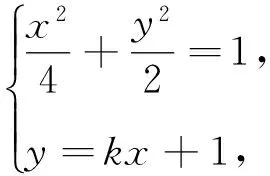
3 推广探究
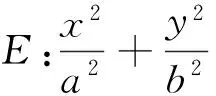

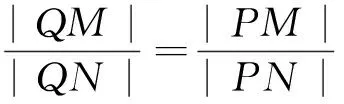
以下证明,对任意的直线l,Q(0,b2)均满足条件.
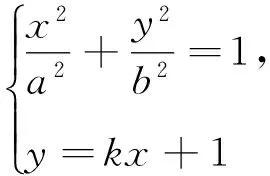
(a2k2+b2)x2+2a2kx+a2-a2b2=0.
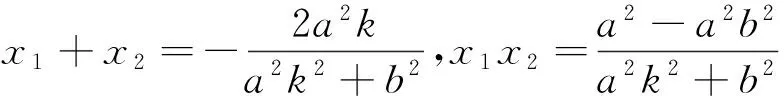
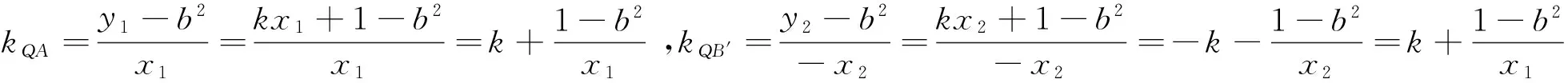
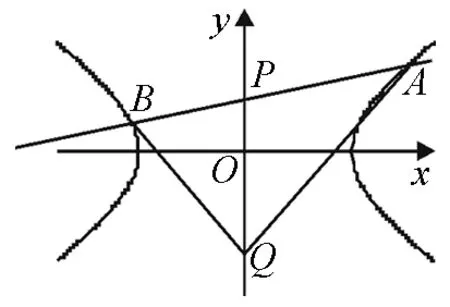
图5

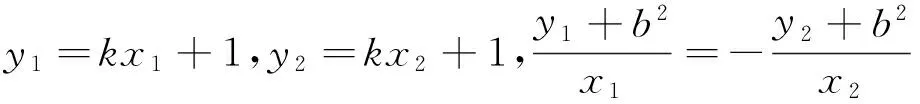
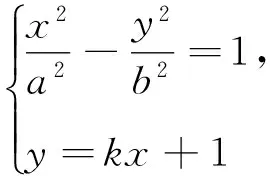
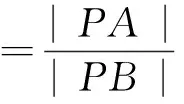
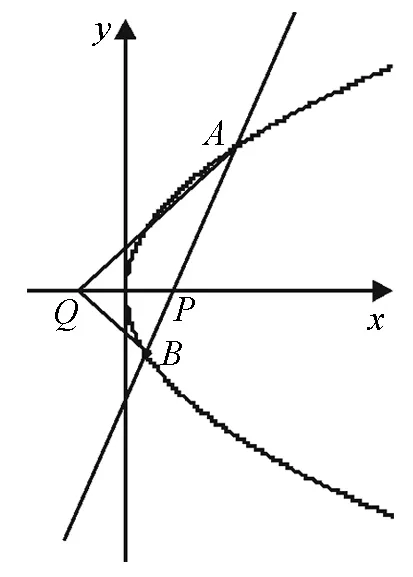
图6
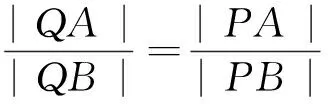
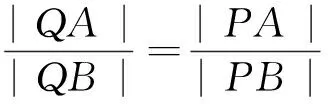
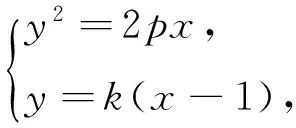
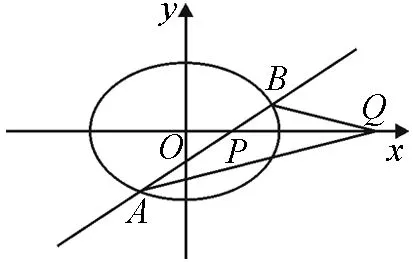
图7
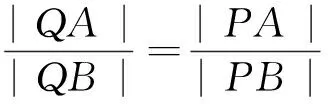
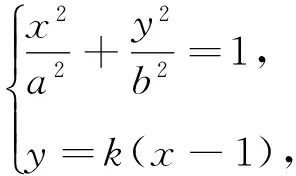
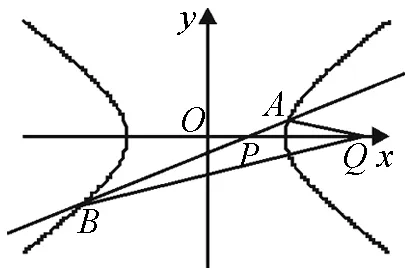
图8
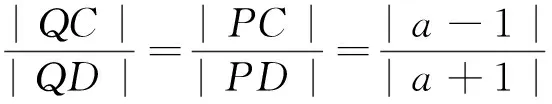
以下证明,对任意的直线l,Q(a2,0)均满足条件.
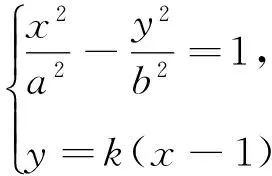
[1]柳俊婷,于兴江,“圆锥曲线的一个性质”再探究[J].中学数学研究(江西),2015,11.
[2]李静,于兴江.一道高考题的多解及推广[J].中学数学研究(江西),2013,12.
[3]孙玉英,于兴江.探究 引申 剖析 启示— 一道高考题的赏析[J].中学数学研究(江西),2013,10.
[4]柳俊婷,于兴江, 2015年山东理科第20题的多解分析及探究[J].中学数学研究(江西),2015,8.
* 作者现为2015级硕士研究生.
猜你喜欢
中学数学杂志(2022年6期)2022-11-18
中学数学杂志(2022年6期)2022-11-17
中学数学杂志(2022年6期)2022-11-14
中学数学杂志(2022年6期)2022-09-05
中学生数理化(高中版.高二数学)(2021年9期)2021-11-05
中学生数理化·高一版(2020年11期)2020-12-14
小学生学习指导(低年级)(2020年10期)2020-11-09
中学生数理化·七年级数学人教版(2019年10期)2019-11-25
新世纪智能(数学备考)(2018年9期)2018-11-08
高中生·天天向上(2018年1期)2018-04-14

