将基本几何性质融入解几运算——从一道调研题谈解析几何的解题教学

江苏省东台市安丰中学　(224221)

杨志青



将基本几何性质融入解几运算
——从一道调研题谈解析几何的解题教学

江苏省东台市安丰中学(224221)

杨志青

1.一道“是非”题

考题在平面直角坐标系xOy中，已知圆C:x2+(y-1)2=5，点A为圆C与x轴负半轴的交点，过A作圆C的弦AB，记线段AB的中点为M，若OA=OM，则直线AB的斜率为_________.

这是2015届南京市、盐城市高三第二次调研考试的第12题(注：填空题共计14道小题，每题5分).考生普遍反映该题运算量太大，时间来不及，只能放弃，因而，这道题的得分率相当低，我校人均得分不足0.5分.

这道题也是这次调研考试后议论的焦点.教师对这道题的褒贬不一，大多数教师认为这道题有点“过分”，对于填空题第12题，大多数考生是要力争完成的，而这道题这么大的运算量，严重影响考生的整场考试，若是第13、14题，还好一点；也有少数教师认为这道题还不错，方法用得巧，很快就能完成.在此，笔者暂不发表个人观点，先谈谈个人的解题认识.

2.解法分析

法一:(解析法)如图1，显然直线AB的斜率存在.设直线AB：y=k(x+2)，代入圆C方程，整理得(1+k2)x2+2k(2k-1)x+4k2-4k-4=0，

图1

解析法是高中数学学习的重点，但用解析法解这道填空题，运算量确实有点大，若是中等难度的解答题，倒差不多.几何法解这道题很简单，但灵活性强，学生的几何性质遗忘多，而且也不是高中学习的重点，考生不易想到几何法.这也是不少教师认为作为填空题不适合的原因.

现在的问题是能不能折中处理：将几何法融入到解析法中去，以此简化运算，并且所使用的几何性质是基本的、学生容易想到的？基于此思考，笔者得出方法三.

法三:先根据题设，运用简单的几何知识，得出一些性质.∵M为弦AB的中点，∴CM⊥AB，∵OA=OM，取AM中点N，则AM⊥ON，∴yM=2yN，ON∥CM.接下来，进行解析运算.

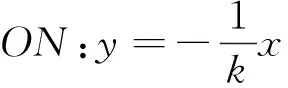
解法三运用了初中最基本的两个几何性质：圆的“垂径定理”与等腰三角形的“三线合一”，高中生对此仍然很熟悉.随后要求解两个二元一次方程组，运算不难.方法三是该调研题自然合理的解法，是对考生有帮助的一种思维方法.基于此，该题作为填空题的第12题，也不能说不合理，笔者甚至认为，这是一道好题！

3.解题教学思考

上述解法三思路并不复杂，为什么考生想不到？不少教师也想不到？文[1]对该题的“多维辨析”的八种方法也未提到该方法，这说明我们很多教师处理解几问题时，思维方法的分割严重，要么解析法、要么几何法，而缺少一种思维意识：将基本几何性质的运用融入到解析运算中去.如此，我们的解析几何的解题教学就存在一点问题了，学生的低得分率也就不足为怪！

解析几何解题教学的核心当然是解析法，主要是用代数运算得到几何结论，而几何法则是由几何性质结合题设推理得出几何结论，这不是解几教学的重点.需要注意的是，解析法与几何法不是不相容的，我们的解题教学可以将几何法融入到解析法中，以减少运算量.

当然，笔者认为几何法融入度不要大，要适度.几何法有时能发挥奇效，教师的分析，学生也能听得懂，但太灵活，碰到具体问题，很多学生还是想不到，效果不会好.我们所期望的是，适度融入最基本的几何性质，如关于圆、三角形、直线等初中教材要求的基本性质，以及高中学习的圆锥曲线的定义，并且在推理时不深挖，目的是得出一些显而易见的结论，为解析法减轻运算.

上述关于解析几何的解题教学的道理很浅显，关键是我们教师要有这种解题意识，并作为一种思考方法在教学中渗透给学生，从而增加解析几何解题教学的实效，切实提高考生解几题的得分率.

4.案例剖析

上述解题教学建议是否合理？实用性强不强？带着这两个问题，笔者对2015年高考数学的全部解几题进行了分析，发现部分试题适当运用几何性质，确实能减少运算量，有助于提高解题速度和运算的准确率.限于篇幅，选取了3道解答题进行剖析说明.

案例1(2015高考新课标Ⅱ卷理科第20题)已知椭圆C:9x2+y2=m2(m>0)，直线l不过原点O且不平行于坐标轴，l与C有两个交点A，B，线段AB的中点为M．

(Ⅰ)证明：直线OM的斜率与l的斜率的乘积为定值；

简析:第(Ⅰ)题用点差法可得斜率之积为-9；第(Ⅱ)题需要选择平行四边形的判定方法，由于线段AB的中点为M，第(Ⅰ)题得到kABkOM=-9，利用这个结论，易想到对角线互相平分的四边形是平行四边形，只要M为OP中点即可.

(Ⅰ)求椭圆E的方程；

(Ⅰ)求椭圆C的方程；

以上3个案例所用到的几何性质不复杂，学生都能轻松发现，问题是学生要有这种适度使用几何法的思维意识，这需要我们教师在解题教学中逐步培养.

[1]徐爱勇.对一道考题的多维辨析与深层思考[J].中学数学教学参考：上旬，2015(7)：32-33.